J'en ai un tout simple, un gâteau parfaitement carré de 31 cm par 31 cm.

Bisous,
Shadock

Une petite faute de frappe que j'ai corrigée 16 dL au lieu de 16 L .

On va dire que c'est la chaleur

Vasimolo

Tu veux dire 96 cm²

Vasimolo

Non , la chaleur n'est pas un paramètre

Je pense que le problème est définitivement corrigé ( j'ai une fâcheuse tendance à changer toutes les données au dernier moment et comme je suis affreusement tête en l'air ... )

Bonne recherche

Vasimolo

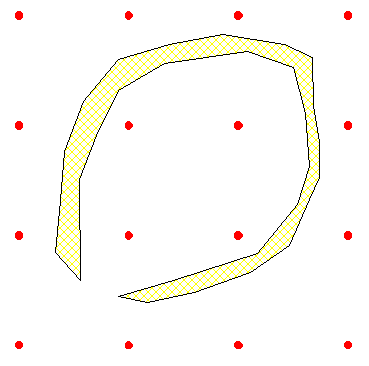
Presque , en fait il s'agit de trouver un gâteau qui ne peut pas éviter les points rouges ( ou montrer que c'est impossible ) .

Vasimolo

L'idée est surement là Gwen mais il va falloir clarifier un peu

Vasimolo

C'est ça Gwen

Vasimolo

Dans ce cas je vais partir sur la démonstration de l'impossibilité!

Je précise un peu la solution de Gwen qui est peu bavard

On place le gâteau n’importe comment sur la paillasse et on expédie par translation chacun des carrés de gâteau dans une seule case . 


Le résultat n’est pas très joli mais on va faire avec .

Un puriste pourrait se demander où vont atterrir les miettes de gâteaux ayant eu la bête idée de paresser sur un côté d'un carré . On peut trancher le problème assez facilement en considérant que seul le coin inférieur gauche et les côtés bas et gauche du carré font partie de la maille ( on peut aussi se dire que l’ensemble de ces points litigieux a une aire nulle et qu'il ne présente donc aucun intérêt ) .

Après , comment exploiter cet enchevêtrement ?

L’aire de base du gâteau qui est initialement de 96 cm² ne risque pas d’augmenter quand on expédie tous les morceaux dans une seule case ( il va même pas mal diminuer à cause des superpositions ) . En bref il y a à l’intérieur de la case qui reçoit tout le monde un point noir qui n'est pas recouvert par les bribes de gâteaux .

On peut aussi imaginer ce même point dans chaque carré de la paillasse .

On décide ensuite de faire glisser le gâteau de façon à ce que le point noir rejoigne un point rouge ( vecteur vert ) .


Après on se dit que si dans sa nouvelle position le gâteau devait chevaucher un point rouge alors dans sa position initiale il devait chevaucher un point noir et là il y a un problème .

Il est d’ailleurs assez curieux de remarquer qu’il n’y a pas besoin de faire tourner le gâteau pour éviter les points rouges : on le pose dans n’importe quelle position et on peut toujours le faire glisser pour éviter les nœuds .

Merci aux participants ( de moins en moins nombreux ) .

Vasimolo

Oui, très intéressant en effet, je n'avais rien vu !

J'essaie de reformuler :

1/ Ton quadrillage est régulier et répétitif. Si on découpe la grille et le gâteau qui la recouvre en petits carrés dont les sommets sont les points de la grille et qu'on les superpose tous, alors on aura :

_Si le gâteau passe par un point sur la grille de départ, alors un des morceau du carré passera par 1 des 4 points du carré obtenu par superposition.
_Sinon, il ne passera pas par 1 des 4 points du carré.
_Et inversement pour les 2 cas


2/ Comme la surface du gâteau fait 96% d'un carré, alors une fois le gâteau découpé, il y aura obligatoirement 1 ou plusieurs trous. Si on déplace par translation le carré de gâteau obtenu de sorte qu'un trou soit face à un point, , en redéployant le gâteau on ne passe plus par aucun point.

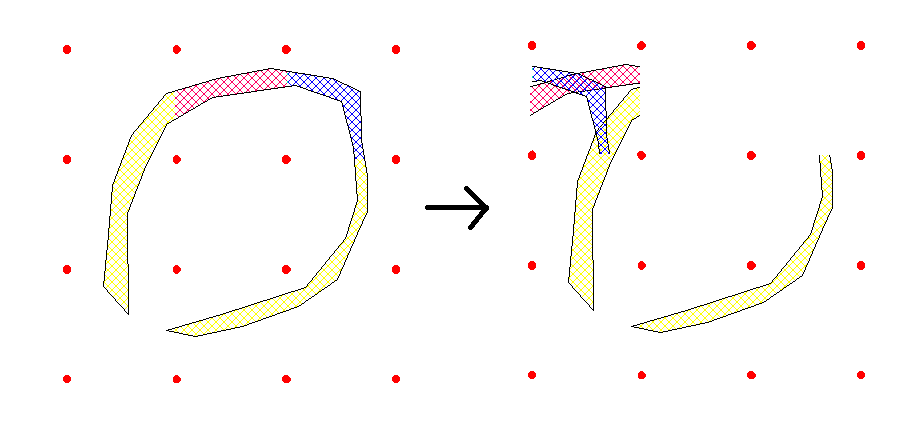
Voici un exemple : (à l'étape 5, j'ai ajouté des carrés à gauche et en dessous)



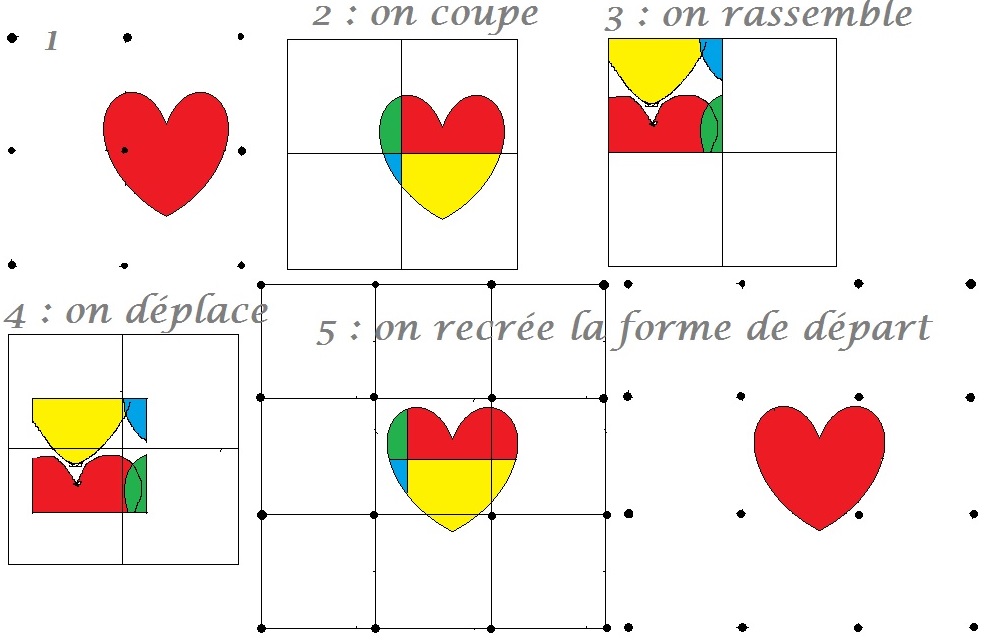
J'espère que c'est plus clair...

En fait mon idée n'était pas celle décrite par Golgot mais ça revient au même

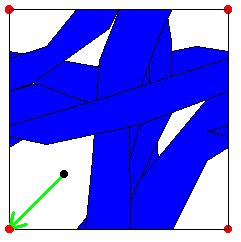
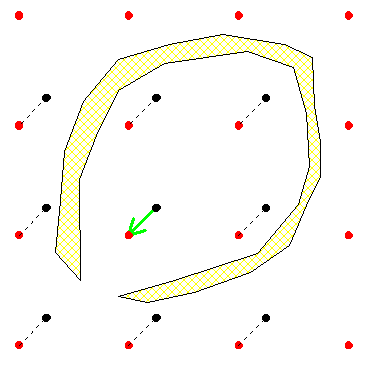
Le début est bien là : on envoie tous les morceaux du cœur dans une seule case et on remarque qu'il y a un point à l'intérieur de la case réceptrice qui n'est recouvert par aucun morceau de cœur : le fameux point noir . Après c'est légèrement différent , on revient au cœur initial et par translation on met un point noir dans chaque carré rouge . La construction des points noirs nous dit que le cœur ne peut chevaucher aucun d’entre eux . On fait ensuite subir au cœur la translation de vecteur vert . Cette translation amène ( bijectivement ) le réseau noir sur le rouge , le nouveau cœur ne peut donc chevaucher aucun point rouge .

J’espère que mon explication est plus claire

Vasimolo