|
#1 - 21-10-2015 20:14:23
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 21-10-2015 22:40:13
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
Gâtaeu 108
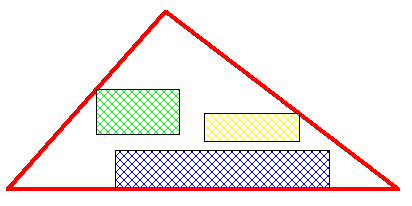
Juste pour savoir... 8kg : on s'en fiche totalement ? Tu veux juste caser 63 rectangles de surface et d'orientation (=à un côté) identique dans un triangle ?
#3 - 21-10-2015 22:54:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 1008
L'orientation de chaque rectangle est la même mais pas la surface ( à priori ) , l'objectif est de récupérer le maximum de gâteau sans s'intéresser à un partage équitable 
Vasimolo
#4 - 21-10-2015 22:58:20
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Gâtaeu 108
Il semblerai qu'un triangle soit homéomorphe à un rectangle du coup... 
Spoiler : [Afficher le message] Je plaisante promis je cherche, en fait je suis intrigué par le 63.
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#5 - 21-10-2015 23:25:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâetau 108
Le 63 est essentiellement un clin d'œil à Bell63 , accessoirement il permet aussi d'obtenir un compte rond 
Vasimolo
#6 - 22-10-2015 02:35:07
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Gâteau 1088
Je me lance un peu vite au risque de dire des bêtises :
On suppose le gâteau de hauteur et densité homogène …
Intuitivement, pour recouvrir un maximum d’espace, il faut coller à la suite des languettes de gâteau. Je ne prouve pas pour le moment que ce soit la solution optimale, j’ai juste essayé de trouver une solution…que j’espère la bonne…
Avec un petit nombre de languettes, on voit trivialement qu’il faut placer ces languettes horizontalement (au sens du dessin de l’exemple) car verticalement, on « perd de la place » à cause du sommet qui sépare.
On considère donc des languettes fines alignées horizontalement.
On se retrouve ainsi avec 63 triangles perdus de chaque côté du triangle plus le petit triangle chapeau en haut.
On note Hi la hauteur (pas forcément égale) des petits triangles perdus et respectivement Gi et Di les largueurs correspondantes. On remarque que le chapeau est en fait un triangle comme les autres mais dont coté gauche et droite se rejoignent.
On a donc :
Perdu = Somme de 0 à 63 de [ ½ * (H(i+1)* (Gi+Di) ]
Il y a un rapport constant entre Gi et Hi (idem pour Di et Hi) défini respectivement atan (alpha) et atan (beta), alpha et beta étant les deux angles « en bas du triangle »
On a donc
Perdu = Somme de 0 à 63 de [ ½ H(i+1)^2*( atan (alpha) + atan (beta)) ]
Mais par propriété élémentaire du triangle atan (alpha) + atan (beta)=Base/H
D’où
Perdu = ½ * Base/H * Somme de 0 à 63 de [ H(i+1)^2 ]
De façon intuitive et probablement connu (est-il besoin de le démontrer ou est-ce admis ? ) :
Somme de 0 à 63 de [ H(i+1)^2 ] avec Somme (Hi)=H et tous les Hi>=0 est minimum quand tous les Hi sont égaux. Donc Hi=H/64
D’où
Perdu = ½ * Base/H * 64 * (H/64)^2 = 1/64 * [Base * H / 2 ]
On reconnait la surface du triangle et on conclu
Perdu = 1/64 du gâteau
Dans ce cas 0.125 kg ce qui tombe assez rond pour que ca puisse être bon, pas trop pour que ça puisse ne pas l'être...
#7 - 22-10-2015 07:51:25
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
Gâteauu 108
J'arrive à 125 g soit 1/64 du gâteau.
#8 - 22-10-2015 08:30:19
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteaau 108
On prend un triangle rectangle et on met toutes les parts orientées comme l'angle droit. L'intérêt de l'angle droit est qu'on ne laisse des espaces que coté hypothénuse.
La 1ère part couvre la moitié du triangle: il ne reste que 2 triangles égaux 4 fois plus petits que l'original.
On remplit de la même façon ces 2 triangles restants.
On divise donc par 2 la surface restante à chaque série de parts.
Les séries successives de parts consomment: 1 puis 2 puis 4...puis 31, soit 63 au total.
La surface résiduelle est de S/2^6=S/64.
Généralité: Avec 2^n-1 parts, on a un reste de S/2^n.
#9 - 22-10-2015 08:53:04
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
Gââteau 108
Salut
Voici mon gâteau
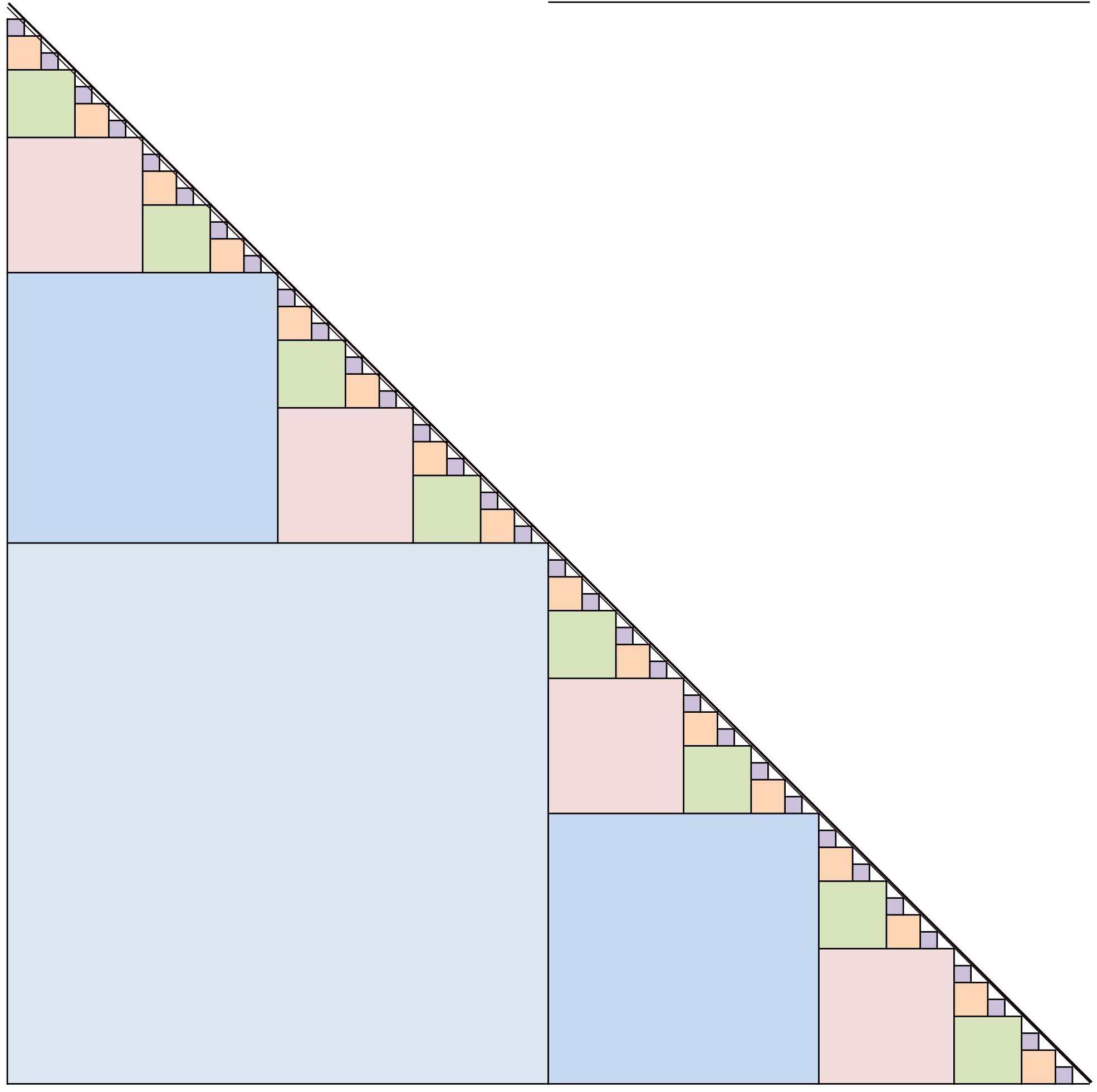
J'ai un doute sur "Chaque part doit présenter un côté parallèle à un côté donné du gâteau ( toujours le même )" et 2 cotés on peut ou pas ??
#10 - 22-10-2015 09:25:47
- fmifmi
- Passionné de Prise2Tete
- Enigmes résolues : 18
- Messages : 87
Gâtea u108
En rangeant des parts carrées dans un triangle rectangle isocèle , ( les diagonales des carrés perpendiculaires à l' hypoténuse ),on obtient:
je ne sais pas faire de dessin
1 carré de surface 1/2,
2 carrés de surface 1/8
4 carrés de surface1/32
....
....
32 carrés de surface 1/2048
Les (2^6 -1 = 63) carrés totalisent une surface de 63/64 ème du total.
on perd 125 Grammes sur 8 Kg
Obelix a une part de 4kg et Idefix doit se contenter d'un biscuit qui pèse à peine 4 grammes
Peut on faire mieux? çà me parait trop facile pour un gateau 108
suite:
Effectivement Vasimolo si le triangle n'est pas rectangle, ça marche aussi.
j'ai réussi a démontrer( pas facile a expliquer sans figure ) que la surface du rectangle est maximum et vaut la moitie de la surface totale si les "sommets" du rectangle sont les milieux des autres cotés.
on en revient a la démonstration ci dessus
1 rectangle de surface 1/2,
2 rectangles de surface 1/8
4 rectangles de surface1/32
....
....
32 rectangles de surface 1/2048
Les (2^6 -1 = 63) rectangle totalisent une surface de 63/64 ème du total.
cqfd.
ce qui est amusant c'est que l'on peut découper les autres parts dans n'importe quel sens( les rectangles n ont pas besoin d’être "paralleles" entre eux) du moment qu'on respecte la condition ci dessus.
tu aurais pu supprimer " (toujours le même) " dans ton énoncé si je ne dis pas de betises?
une faille dans mon raisonnement j'ai toujours raisonné avec un coté du rectangle "posé" sur le plus grand coté du triangle. j'ai la flemme de le démontrer dans les autres cas!
#11 - 22-10-2015 09:45:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 018
@Portugal : c'est ça , on peut faire un peu plus court dans la rédaction mais l'idée est bien là 
@Gwen : pour quel triangle et pourquoi ne peut-on pas faire mieux ?
@Nodgim , Nobodydy et Fmifmi : et si le triangle n'est pas rectangle ?
Il y a une démonstration extrêmement courte et générale du résultat .
Vasimolo
#12 - 22-10-2015 10:40:55
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
gâtzau 108
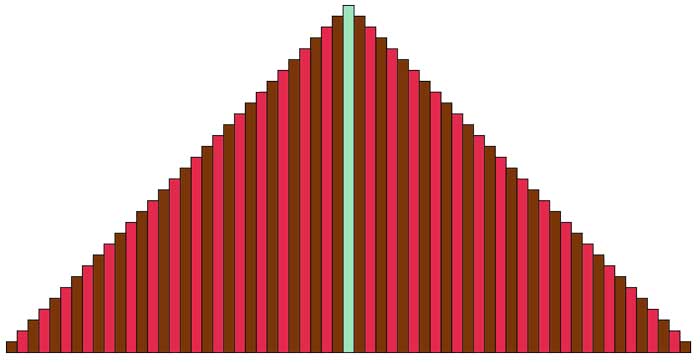
Voici
un chocolat, coulis de fraise pistache 
#13 - 22-10-2015 11:29:57
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
hâteau 108
Je me réserve la part centrale ( non , je ne suis pas fan de pistache  ) )
Vasimolo
#14 - 22-10-2015 11:49:19
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâteau 1008
Je découpe le gâteau en 64 bandes parallèles au plus grand côté (*), toutes de même hauteur(**).
Dans chaque bande (sauf celle du haut sur la figure), on peut loger un rectangle, cela fera en tout 63 parts, il reste aux extrémités deux morceaux (***) qui représentent ensemble l'homothétique du triangle d'origine dans le rapport 1/64, donc de surface 1/64² chacun.
Les 128(***) morceaux perdus pèsent 8/64kg soit 125 grammes.
* Le choix du côté du triangle initial n'a pas d'importance sauf s'il et obtusangle,
auquel cas il faut choisir le plus grand côté.
** Si les 64 bandes n'ont pas toutes la même hauteur, on perd plus.
*** un morceau, 64 en tout, si le triangle est rectangle et que l'on a coupé parallèlement à un côté de l'angle droit.
EDIT suite à réflexion de Vasimolo
** est facile à démontrer, chaque découpe devant être à égale distance de ses deux voisines. (Ça c'est facile)
#15 - 22-10-2015 12:26:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâtzau 108
@Halloduda : c'est pas faux ( comme disait l'autre ) mais on affirme beaucoup et on démontre peu 
Vasimolo
#16 - 22-10-2015 13:08:35
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâtteau 108
On empile sur la base B 64 rectangles d'épaisseur H/64 (H hauteur du triangle) et de longueur B. On tronque ces rectangles avec les 2 autres cotés du triangle. Des 64 retangles initiaux, il n 'en reste plus que 63. Les parties non couvertes sont 1 triangle en haut + 63 demi triangles ( en regroupant=63 triangles) donc 64 triangles identiques, format réduit du triangle initial.
S petit triangle: (H/64*B/64)/2
S perdue: 64*(H/64)*(B/64)/2=HB/64/2=S grand triangle/64.
C'est donc indépendant du triangle.
On se rend compte qui si les rectangles ne sont pas tous d'épaissseur identique, la partie perdue est plus importante. Ceci est dû au fait que la partie perdue dépend du carré de la hauteur du rectangle. Car une suite de nombres à somme constante a une somme de carrés minimale quand les nombres sont égaux.
#17 - 22-10-2015 14:37:33
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
âGteau 108
Pour celui-ci :

#18 - 22-10-2015 16:27:57
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
gâtezu 108
@Nodgim , Nobodydy et Fmifmi : et si le triangle n'est pas rectangle ?
Comme mon niveau de math est limité et que je me suis déjà fait avoir plusieurs fois sur tes gâteaux 
je répondrais que si le triangle n'est pas rectangle, cela ne marche pas aussi bien 
Te connaissant, J'ai une chance non négligeable pour que la solution ne soit optimale que dans un triangle rectangle mais je peux me planter. 
Dans un triangle ABC rectangle en A, l'aire max d'un rectangle AMNP est atteinte quand MNP sont au centre des cotés du triangle. (donc la perte est minimale)
on trouve 1 rectangle, ce qui forme 2 nouveaux triangles dans la figure , etc...
nous pouvons positionner 63 rectangles (1, 2, 4, 8, 16 et 32).
C'est Optimal....
Dans un autre triangle qui peut se décomposer en 2 triangles rectangles, les 63 rectangles rentreront différemment mais la perte sera plus importante.
#19 - 22-10-2015 16:42:09
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gâteau 10
bonjour.
si le gâteau a une base B et une hauteur associée H
Je coupe les 63 gâteaux comme ceci:
10 lignes de gâteaux de même largeur h = H/11(ou hauteur)
première ligne en haut 1 part
seconde ligne en dessous 2 parts (ces 3 parts ont une base b = B/11
troisième ligne en dessous 4 parts (ces parts ont une base 3b/4
quatrième ligne en dessous 5 parts (ces parts ont une base 4b/5
cinquième ligne en dessous 6 parts (ces parts ont une base 5b/6
...........................
dixième ligne et la dernière 11 parts (ces parts ont une base 10b/11
il y a bien 1+2+4+5+6+7+8+9+10+11 = 63 parts
la perte serait de 8/11 kg un onzième du gâteau.
l'aire du gâteau A = 121bh/2
en sommant les lignes de gâteaux la totalité des surfaces de parts consommées
C = 3bh + 3bh +4bh + 5bh + 6bh + 7bh + 8bh + 9bh + 10bh = 55bh = 110bh/2
ainsi 11bh/2 ne sera pas consommée. donc 1/11 du gâteau il me semble.
#20 - 22-10-2015 20:09:32
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
GGâteau 108
Salut !
Je choisi au hasard une base. Je découpe par des lignes parallèles régulièrement espacées de 1/64ème de la hauteur du triangle.
La ligne la plus proche de ma base coupe les 2 côtés en 2 points qui me permettent de former un rectangle en rejoignant la base.
La 2ème ligne la plus proche de la base coupe les 2 côtés en 2 points qui me permettent de former un rectangle en rejoignant ma 1ère ligne.
Et ainsi de suite jusque la 63ème ligne.
Il me reste alors un petit triangle près du sommet, ainsi que 63 autres identiques si je rassemble les 2 petit morceaux aux extrémités de chaque rectangle.
Chaque petit triangle est semblable au grand et a ses dimensions 64 fois plus petite, donc une aire 64² fois inférieure à l'aire du triangle de départ. Il y en a 64 donc le triangle aura perdu 64/64²=1/64ème de sa masse, soit 0.015625kg=15.625g
Du coup, peut importe la forme de départ du gâteau...
Je ne sais pas comment démontrer que c'est optimal, ni d'ailleurs si c'est optimal, mais je trouve la perte tout à fait raisonnable et la construction aisée !
#21 - 22-10-2015 20:48:41
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
âGteau 108
Bonsoir,
Quelle que soit la forme du triangle, j'obtiens une perte de 125 g (8 kg / 64).
Je découpe la hauteur du triangle en 64 segments égaux, ce qui va déterminer 63 parts de plus grande largeur possible, avec un petit triangle perdu de chaque côté, et un triangle vide au sommet du triangle initial.
#22 - 22-10-2015 23:06:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#23 - 23-10-2015 10:07:46
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
gâteay 108
Non, il y en a plein d'autres, du moment que l'on garde ces 63 noeuds sur la diagonale.
Ces noeuds déterminent des demi carrés obligatoirement exclus. La somme de ces distances est constante quels que soient les noeuds choisis. Il faut donc minimiser la somme de leurs carrés.
Ils existent obligatoirement sauf le cas idiot d'un rectangle qui pourrait être prolongé et ne l'a pas été.
S'il y en a 2 espacés différemment, on peut encore optimiser en les égalisant. Donc c'est optimal avec un espacement régulier.
S'il y en a moins de 63, la somme des carrés augmentera.
Si un autre angle était choisi, la surface perdue serait plus importante (carré optimal par rapport au rectangle en terme de surface) Le triangle rectangle isocèle est donc celui qui permet le moins de pertes vu que sa diagonale est minimale.
Et enfin, comme la solution choisie couvre tout le reste du triangle, elle est optimale.
#24 - 23-10-2015 11:16:52
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Gâteau 1108
Avec une part unique, il est facile de démontrer qu’on a le moins de perte avec une largeur de part faisant la moitié de la hauteur du gâteau.
Avec deux parts pas forcément de même largeur, ça se complique un peu.
Alors avec 63 .....
#25 - 23-10-2015 11:43:46
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 180
Ce n'est pas si difficile Franky , observe bien les chutes 
Vasimolo
|
 |

 Accueil
Accueil
 Forum
Forum