 |
#1 - 13-10-2013 16:44:44
- housseyne
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 26
#2 - 13-10-2013 17:35:21
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
Geometrie aveec des oeufs
Bienvenue à vous sur le forum. Je me permets de vous demander si c'est une énigme ou un devoir maison que vous nous proposez. Dans les 2 cas, je n'ai pas la solution.
#3 - 13-10-2013 17:52:53
- housseyne
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 26
geometrie avec des peufs
SabanSuresh
non, ma spécialité est génie électrique ;mais malgré ça j'aime la geométrie;
et si tu veux la répense je peut te la donner par un sms
#4 - 13-10-2013 19:45:39
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
geometeie avec des oeufs
Je ne comprends même pas la question 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#5 - 13-10-2013 19:48:54
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
Geometrie aavec des oeufs
Vous pouvez m'appeler Saban tout court. Je posais cette question car de nombreuses personnes viennent demander de l'aide pour leurs DM et partent dès que la solution ait été donnée et la plupart du temps, ce sont des nouveaux avec 0 énigmes résolues et quelques messages seulement. Je suis désolé si je vous ai offenser.
En ce qui concerne l'énigme, vous pouvez la modifier en fixant une période x (entre 1 et 255 h) durant laquelle les réponses seront cachées. Comme cela, plusieurs personnes peuvent répondre et vous serez le seul à voir les réponses.
Edit : Moi non plus, je n'ai pas compris la question. 
#6 - 13-10-2013 20:41:58
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
geoletrie avec des oeufs
Je pense avoir compris. On a une succession de N oeufs elliptiques. Quand N tend vers l'infini, les dimensions du N-ième oeuf tendent vers zéro, mais la valeur de la longueur totale du train d'oeufs tend vers une valeur finie. Laquelle ?
J'ai commencé par calculer la distance entre le centre du 1er oeuf et celui du 2ème, mais je me suis perdu dans de lourds calculs qui m'ont donné mal à la tête.
J'y reviendrai plus tard: affaire à suivre ...
#7 - 13-10-2013 21:35:55
- Fito11235
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 173
Geometrie aavec des oeufs
Ca ressemble à un histoire de maximum. La longueur de l'ensemble des oeufs est une suite croissante. Cette suite admet-elle un maximum (auquel cas on aurait la plus courte longueur jamais atteinte)?
Si c'est cela. Il suffit d'étudier la série:
2a + a + a/2 + .... + a/2^n+..... =2a +a x (Somme n=1 à infini de (1/2)^n)
Cette série est bien convergente mais mes souvenirs de fac sont trop loin, je ne suis plus sûr elle doit converger vers 2 il me semble ce qui donnerait une longueur minimale de 4a.
#8 - 13-10-2013 21:41:00
- housseyne
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 26
geometrie avec ded oeufs
saban
pas de probléme 
merci
si tu concentre alors tu vas comprendre
Bon chance.
#9 - 13-10-2013 22:00:11
- housseyne
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 26
Geometrrie avec des oeufs
Fito11235 a écrit:Ca ressemble à un histoire de maximum. La longueur de l'ensemble des oeufs est une suite croissante. Cette suite admet-elle un maximum (auquel cas on aurait la plus courte longueur jamais atteinte)?
Si c'est cela. Il suffit d'étudier la série:
2a + a + a/2 + .... + a/2^n+..... =2a +a x (Somme n=1 à infini de (1/2)^n)
Cette série est bien convergente mais mes souvenirs de fac sont trop loin, je ne suis plus sûr elle doit converger vers 2 il me semble ce qui donnerait une longueur minimale de 4a.
Bienvenu:)
la langueur AB est un sup non max parce que le appartient à l'ensemble des langueurs atteintes (s'elle existe)."d'après les premiers cours d'Analyse de 1er année".
La réponse est fausse.
#10 - 13-10-2013 22:03:24
- Fito11235
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 173
geometriz avec des oeufs
Ah oui borne sup, ca me revient maintenant. je ne trouvais plus le terme  . .
D'accord pout ma réponse fausse, lecture trop rapide de la figure! erreur grossière 
#11 - 13-10-2013 22:16:38
- housseyne
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 26
Geometrie avec de soeufs
Franky1103 a écrit:Je pense avoir compris. On a une succession de N oeufs elliptiques. Quand N tend vers l'infini, les dimensions du N-ième oeuf tendent vers zéro, mais la valeur de la longueur totale du train d'oeufs tend vers une valeur finie. Laquelle ?
J'ai commencé par calculer la distance entre le centre du 1er oeuf et celui du 2ème, mais je me suis perdu dans de lourds calculs qui m'ont donné mal à la tête.
J'y reviendrai plus tard: affaire à suivre ...
-------------------------------------------------------------
Oui c'est ça
tu as comprend le problème
mais le problème n'est pas trop compliqué il suffit un BON IMAGINATION
#12 - 13-10-2013 22:20:06
- housseyne
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 26
#13 - 13-10-2013 22:53:24
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Geometrie avec des eoufs
Je prend un repère centré sur la première ellipse avec l'axe Oy vers le bas (pour avoir des valeurs positives) et j'appelle m l'abscisse du centre de la seconde ellipse.
Equation première ellipse: (x/a)²+(y/b)²=1
Equation seconde ellipse: [(x-m)/(a/2)]²+[(y-b/2)/(b/2)]²=1
Par simplification je pose: X=x/a; Y=y/b et k=m/a
Equation première ellipse: X²+Y²=1, qui donne Y=V(1-X²)
Equation seconde ellipse: (X-k)²+(Y-1/2)²=1/4
Je cherche maintenant l'intersection de ces deux ellipses, ce qui va me donner m.
Je trouve: (4k²+1).X²-4k(k²+1).X+k²(k²+2)=0
Pour avoir une racine double en X, le discriminant D doit être nul:
D/4=4k²(k²+1)²-k²(k²+2)(4k²+1)=0, ce qui donne après développement:
D/4=-k²(k²-2), d'où: k=V2
AB/a=(V2)+(V2)/2+(V2)/4+(V2)/8+...+(V2)/(2^n)
soit: AB/a=(V2).[1/2+1/4+1/8+...+1/(2^n)]
dont la limite (pour n infini) est: AB/a=2V2, d'où: AB=2V2.a
Le train d'oeufs complet a une longueur de: a+AB=(1+2V2).a
#14 - 14-10-2013 00:46:17
- housseyne
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 26
Geometrie avec des oeuf
Franky1103
Excellent
Solution purement Analytique
#15 - 14-10-2013 04:39:17
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
geomeyrie avec des oeufs
Je pense que c'est [latex]AB=2\sqrt2 *a[/latex]
En effet, distordons verticalement pour avoir des cercles.
La distance horizontale entre les centres de deux cercles consécutifs
ayant pour rayons 2 et 1 est [latex]\frac{\sqrt{3²-1²}}1[/latex]
Le point limite B est le centre commun à toutes les homothéties.
#16 - 14-10-2013 08:46:47
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
Geomerie avec des oeufs
Bonjour,
Le problème devient très simple quand on procède à une homothétie verticale pour transformer les œufs en cercles :
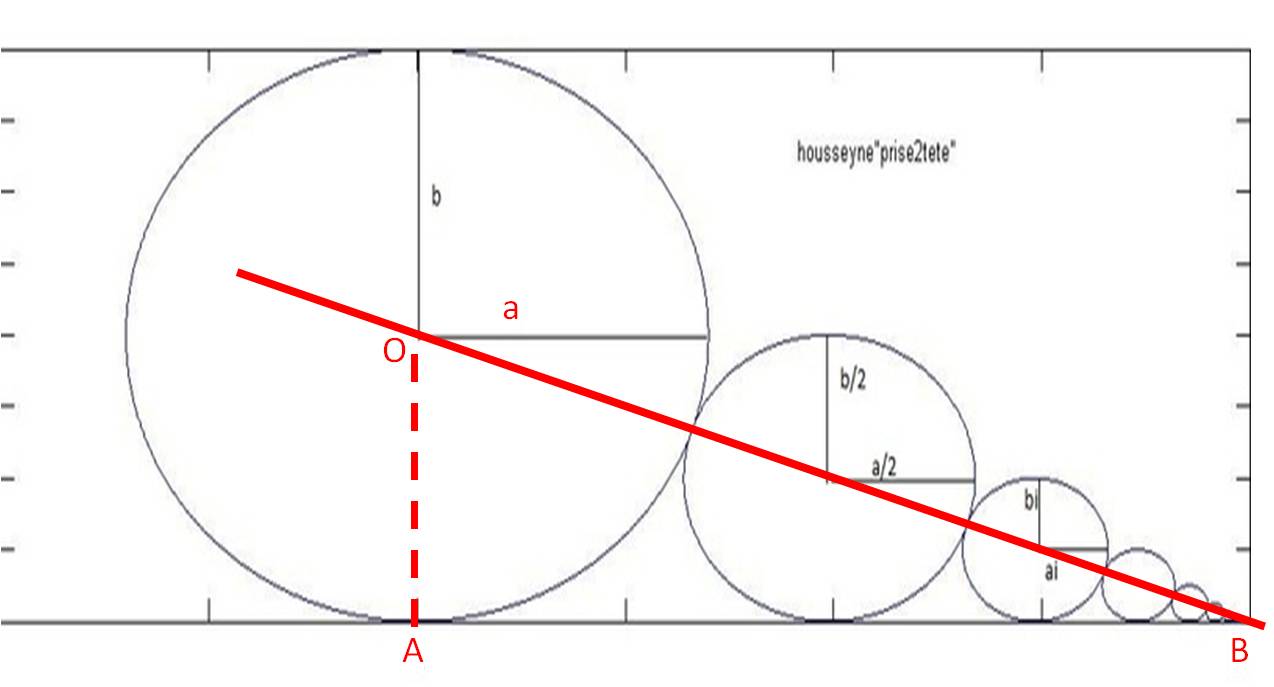
La longueur AB cherchée vaut racine(OB² - OA²)
avec OA² = a²
et OB² = a²[1+ 2(1/2+1/4+1/8+...)]² = a² x [1+2]² = 9a²
Donc AB = 2racine(2)a
Klim.
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#17 - 14-10-2013 10:27:00
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
geometroe avec des oeufs
Bonjour !
Par affinité orthogonale on se ramène à des cercles, ce qui ne change pas [latex]AB[/latex].
Notons [latex]c[/latex] la distance du centre du 1er cercle au point supérieur du second cercle.
Par Pythagore on a la relation
[TeX]c^2=\left(a+\frac{a}{2}\right)^2-\left(\frac{a}{2}\right)^2[/TeX][TeX]c^2 = \left(\frac{9}{4}-\frac{1}{4}\right)a^2[/TeX][TeX]c^2 = 2a^2[/TeX][TeX]c = a\sqrt{2}[/TeX]
Alors on a
[TeX]AB=c+\frac{c}{2}+\frac{c}{4}+\cdots+ \frac{c}{2^n}+\cdots[/TeX]
[TeX]AB=2c[/TeX][TeX]AB=2a\sqrt{2}[/TeX]
Voilà !
#18 - 14-10-2013 10:38:32
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
heometrie avec des oeufs
Proposition
De manière générale, l'équtation d'une ellipse est:
[TeX]\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{2*x_0*x}{a^2}-\frac{2*y_0*y}{b^2}+\frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}-1=0[/TeX]
où [latex]x_0[/latex] et [latex]y_0[/latex] sont les coordonnées du centre de l'ellipse.
Mon objectif est de calculer la distance entre les centres des 2 premières ellipses, pour cela j'ai déterminé l'équation des ces dernières.
La première ellipse:
[TeX]x_0=0[/latex] et [latex]y_0=b[/latex];
[latex]\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{2*b*y}{b^2}=0[/latex] soit [latex]|y-b|=b*\sqrt(1-x^2/a^2)[/TeX]
En considérant la partie inférieure de l'ellipse (c'est la partie en contact avec la 2ème ellipse), on a: [latex]y_1=b-b*\sqrt(1-x^2/a^2)=b-b*\sqrt(1-x^2)[/latex] pour [latex]a=1[/latex] (pour simplifier les calculs)
[TeX]\frac{dy_1}{dx}=\frac{b*x}{\sqrt{1-x^2}}[/TeX]
La deuxième ellipse:
[TeX]x_0=\alpha[/latex] et [latex]y_0=b/2[/latex] où [latex]\alpha[/latex] est la distance entre les centres des 2 premières ellipses.
On arrive après calcul à [latex]|y-b/2|=b*\sqrt{-x^2+2\alpha*x-\alpha^2-1/4}[/TeX]
Pour cette 2è ellipse, on va considérer la partie suppérieure (partie en contact avec la première ellipse) donc: [latex]y_2=b/2+b*\sqrt{-x^2+2\alpha*x-\alpha^2-1/4}[/latex].
[TeX]\frac{dy_2}{dx}=\frac{b*(-x+\alpha)}{\sqrt{X}}[/latex] où [latex]X=-x^2+2\alpha*x-\alpha^2-1/4[/TeX]
Au point de contact, on a 2 conditions:
- les deux ellipses ont la même la tangente donc [latex]\frac{dy_1}{dx}=\frac{dy_2}{dx}[/latex]
- [latex]y_1=y_2[/latex].
Cela donne un système de 2 équations à 2 inconnus ([latex]x[/latex] et [latex]\alpha[/latex]).
Tout calcul bien fait, on a:
[TeX]x=2\sqrt{2}/3[/TeX]
[TeX]\alpha=3*x/2=\sqrt{2}[/latex].
Pour un a quelconque [latex]\alpha=\sqrt{2}*a[/latex].
la distance AB cherchée est la somme des [latex]\alpha_i[/latex] qui est une suite géométrique de premier terme [latex]\sqrt{2}*a[/latex] et de raison [latex]1/2[/latex] d'où
[latex]AB=2*\sqrt{2}*a.[/TeX]
CQFT 
#19 - 14-10-2013 22:59:55
- fmifmi
- Passionné de Prise2Tete
- Enigmes résolues : 18
- Messages : 87
Geometrie avc des oeufs
la suite est finie, c'est évident puisque la somme des (1/2)^n lorsque n tend vers l'infini tend vers 2 et que les centres des deux ellipses sont plus rapprochées que si leur centre se situait la meme droite.
Le probleme et je n'y arrive pas est le delta X deux ellipses!
tout ce que je peut dire c'est que d<2a, a etant le grand axe de la premiere ellipse.
#20 - 16-10-2013 01:39:00
- housseyne
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 26
grometrie avec des oeufs
Klimrod
Excellant réponse
meme solution avec moi
Bravo
halloduda
réponse vrai
Merci
masab
Meme réponse que Klimord
vous avez bien compris et imaginer le probléme
Bien
kossi_tg
Bravo
c'est la 3eme Solution que je veux
le point important c'est l'égalité des dérivées.
Merci
fmifmi
Oui c'est ça le problème
A la prochaine foie avec nouvelle casse tète
EDIT modération (ash00) : le multipost d'affilée est considéré comme du spam.
Ici, 6 messages d'affilée c'est un record. Le prochain record, si tu réitères ce genre de chose, est une grosse claque sur tes fesses un avertissement super méchant !
#21 - 16-10-2013 04:42:48
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
heometrie avec des oeufs
Cette homothétie verticale qui transforme les ellipses en cercles est astucieuse. Je ne l'ai pas vue, mais j'aurais dû m'en douter, puisque le petit axe disparait rapidement dans mes lourds calculs.

#22 - 16-10-2013 10:58:30
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
heometrie avec des oeufs
Je peux me permettre de râler contre ce SEXTUPLE post ?!
Merci de tout mettre en un seul message la prochaine fois 
A part ça, la solution est redoutable de facilité, c'en est blasant. Par contre, j'ai peut-être raté ce détail : comment prouve-t-on l'alignement de tous les centres ?
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#23 - 16-10-2013 16:02:17
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
geomeyrie avec des oeufs
On peut procéder ainsi pour prouver que les centres sont alignés avec B.
On note I le centre d'homothétie des 2 premiers cercles (c'est le point d'intersection des 2 tangentes communes aux cercles). On sait que la droite passant par les centres de ces 2 cercles passe aussi par I.
L'homothétie de centre I de de rapport 1/2 transforme le 1er cercle en le second cercle, et le second cercle en le 3ème cercle, etc
Par suite les 2 tangentes sont communes à tous les cercles.
Et de plus B=I.
#24 - 16-10-2013 20:52:00
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
geometrie avzc des oeufs
Merci beaucoup 
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#25 - 17-10-2013 10:47:31
- housseyne
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 26
GGeometrie avec des oeufs
Bien masab
et on peut aussi calculer AB "pour eviter la somme geometrique " comme la suite:
soit O1 et D les centres des premiers cercles et p la projection de D sur AO
en connaissant la distance entre les premiers cercles = V2*AO
alors
tan(OA,OB)=PO/OP=AB/OA ==>AB=OA*PO/OP
PO=V2*AO
OP=AO-AO/2=AO/2
Donc : AB=2*V2*AO
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum








