|
#26 - 01-06-2014 21:01:32
#27 - 02-06-2014 05:31:09
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
gâteai 78
J'ai une démonstration pour 7 points :
Définition : Pour deux points [latex]A[/latex] et [latex]B[/latex] recouverts par un gâteau, je définis le triangle [latex]T_{AB}[/latex] qui est le plus petit triangle équilatéral qui a la même orientation que le gâteau et qui recouvre les points [latex]A[/latex] et [latex]B[/latex].
On peut construire ce triangle en traçant les parallèles à chaque côté passant par [latex]A[/latex] et par [latex]B[/latex].
Par exemple dans la figure ci-dessous [latex]T_{AB}[/latex] est représenté par le triangle violet :
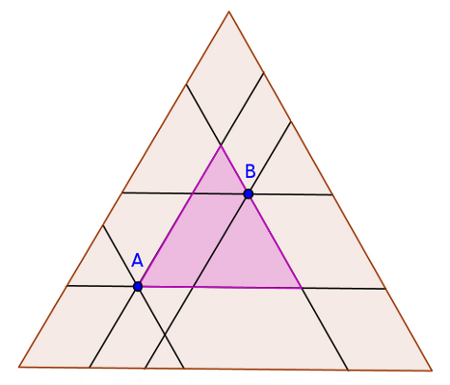
Ce triangle vérifie la propriété suivante :
Lemme 1: Pour tout point [latex]x\in T_{AB}[/latex], si un gâteau recouvre les points [latex]A[/latex] et [latex]B[/latex] alors il recouvre aussi [latex]x[/latex].
C'est évident, si ce n'était pas le cas, on pourrait facilement trouver un triangle équilatéral qui recouvre [latex]A[/latex] et [latex]B[/latex] et qui est plus petit que [latex]T_{AB}[/latex] puisqu'il ne contiendrait pas x.
On a une deuxième propriété similaire qui concerne les triangles quelconques :
Lemme 2 : Soit [latex]D,E[/latex] et [latex]F[/latex] trois points du plan, alors pour tout point [latex]x[/latex] appartenant au triangle [latex]DEF[/latex], si un gâteau recouvre les trois points [latex]D, E[/latex] et [latex]F[/latex], alors il recouvre x.
C'est trivial. (Une autre façon de montrer le lemme 1 est de voir que c'est un corollaire du lemme 2.)
Maintenant, nous allons montrer le théorème suivant :
Théorème : Pour tout ensemble de 4 points qui peut être recouvert par un gâteau, il existe 3 points parmi ces quatre qui vérifient la propriété suivante : Si un gâteau recouvre ces trois points, alors il recouvre le quatrième.
Preuve :
Spoiler : [Afficher le message]
Soit donc [latex]A,B,C[/latex] et [latex]D[/latex] quatre points pouvant être recouvert par un gâteau.
Expliquons avec un shéma :
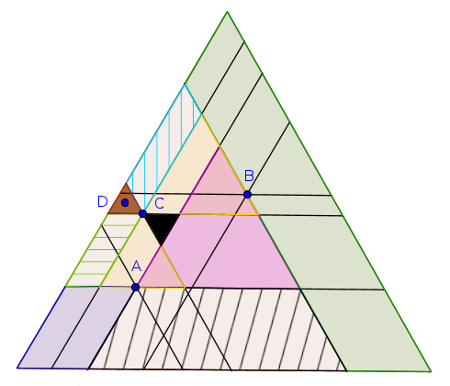
On trace d'abord [latex]T_{AB}[/latex] (en violet). Ensuite on a plusieurs cas :
-Le point [latex]C[/latex] appartient à [latex]T_{AB}[/latex]. Alors où que soit le point [latex]D[/latex], d'après le lemme 1, si un gâteau recouvre [latex]A,B[/latex] et [latex]D[/latex] alors il recouvre C. CQFD.
-Le point [latex]C[/latex] est dans la partie verte. Alors dans ce cas, on a forcément [latex]B\in T_{AC}[/latex]. Et donc où que soit le point [latex]D[/latex], d'après le lemme 1, si un gâteau recouvre [latex]A,C[/latex] et [latex]D[/latex] alors il recouvre B. CQFD.
-Le point [latex]C[/latex] est dans la partie bleue (non hachuré en bas à gauche). Alors dans ce cas, on a forcément [latex]A\in T_{BC}[/latex]. Et donc où que soit le point [latex]D[/latex], d'après le lemme 1, si un gâteau recouvre [latex]B,C[/latex] et [latex]D[/latex] alors il recouvre A. CQFD.
La discussion ci-dessus est valable également pour le point [latex]D[/latex] (on inverse les rôles de [latex]C[/latex] et [latex]D[/latex] (sauf dans le CQFD évidemment  )). )).
Donc pour les points [latex]C[/latex] et [latex]D[/latex] il ne reste plus à étudier le cas des deux régions trapézoïdales qui restent. Pour le point [latex]C[/latex], j'ai choisit une des deux, on aura un raisonnement similaire pour l'autre région.
Donc plaçons le point [latex]C[/latex] dans une des deux régions trapézoïdales.
Les triangles jaunes correspondent à [latex]T_{AC}[/latex] et [latex]T_{BC}[/latex]. Il ne reste plus qu'a étudier les cas pour le point [latex]D[/latex] :
-Le point [latex]D[/latex] appartient à [latex]T_{AC}[/latex]. Alors d'après le lemme 1, si un gâteau recouvre [latex]A,C[/latex] et [latex]B[/latex] alors il recouvre D. CQFD.
-Le point [latex]D[/latex] appartient à [latex]T_{BC}[/latex]. Alors d'après le lemme 1, si un gâteau recouvre [latex]B,C[/latex] et [latex]A[/latex] alors il recouvre D. CQFD.
-Le point [latex]D[/latex] appartient au trapèze hachuré en noir. Alors dans ce cas, on a forcément [latex]A\in T_{DC}[/latex]. Et donc d'après le lemme 1, si un gâteau recouvre [latex]D,C[/latex] et [latex]B[/latex] alors il recouvre A. CQFD.
-Le point [latex]D[/latex] appartient à la zone hachuré bleue. Alors dans ce cas, on a forcément [latex]C\in T_{AD}[/latex]. Et donc d'après le lemme 1, si un gâteau recouvre [latex]A,D[/latex] et [latex]B[/latex] alors il recouvre C. CQFD.
-Le point [latex]D[/latex] appartient à la zone hachuré verte. Alors dans ce cas, on a forcément [latex]C\in T_{BD}[/latex]. Et donc d'après le lemme 1, si un gâteau recouvre [latex]B,D[/latex] et [latex]A[/latex] alors il recouvre C. CQFD.
-Le point [latex]D[/latex] appartient au triangle noir. Alors dans ce cas [latex]D[/latex] est à l'intérieur du triangle [latex]ABC[/latex]. Et donc d'après le lemme 2, si un gâteau recouvre [latex]A,B[/latex] et [latex]C[/latex] alors il recouvre D. CQFD.
Et enfin le cas de la figure :
-Le point [latex]D[/latex] appartient au triangle marron. Alors dans ce cas [latex]C[/latex] est à l'intérieur du triangle [latex]ABD[/latex]. Et donc d'après le lemme 2, si un gâteau recouvre [latex]A,B[/latex] et [latex]D[/latex] alors il recouvre C. CQFD.
Dans tous les cas, il existe toujours trois des quatres points qui lorsqu'ils sont recouverts, alors le quatrième l'est aussi. QED.
Non,non je vous assure ce n'est pas compliqué. C'est long parce qu'il y a beaucoup de cas, mais ce n'est pas compliqué. 
Bon revenons à nos tâches 
Nous voulons montrer que si n'importe quel groupe de sept taches peut être recouvert par les deux gâteaux alors on peut recouvrir toutes les taches.
Raisonnons par récurrence sur le nombre de taches.
Si il n'y a que 7 taches, alors c'est évident.
Maintenant supposons que ce soit vrai pour n'importe quel ensemble de n+7 taches. Montrons que c'est vrai pour un ensemble de n+8 taches.
-Parmi ces n+8 taches, prenons un ensemble de 7 taches.
-On sait que l'on peut recouvrir ces 7 taches avec les deux gâteaux.
-Par le principe des tiroirs il y a forcément un gâteau qui recouvre au moins 4 de ces taches (d'où le 7).
-Parmi ces 4 taches, d'après le théorème je sais qu'il en existe une qui sera automatiquement recouverte si les trois autres sont recouvertes. Appelons cette tache t.
-D'après l'hypothèse de récurrence je peux recouvrir les n+7 autres taches, et donc le théorème me dit que la tache t est automatiquement recouverte. On a donc trouver un recouvrement des n+8 taches. Qed.
EDIT : HAAAAAAAAA...., Non non non mais non  ! Ceci ne marche que si mes quatre taches sont recouvertes par un seul gâteau, et rien assure que le recouvrement donné par l'hypothèse de récurrence vérifie cette propriété ! ! Ceci ne marche que si mes quatre taches sont recouvertes par un seul gâteau, et rien assure que le recouvrement donné par l'hypothèse de récurrence vérifie cette propriété !
C'est encore foireux 
Pourtant, pourtant, pourtant..., mais non  . .
Il y a sûrement plus simple.
#28 - 02-06-2014 22:33:16
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteeau 78
C'est compliqué tout ça Cogito , il doit bien y avoir une idée simple cachée la dessous mais je ne fais pas mieux que toi pour le moment 
Vasimolo
#29 - 03-06-2014 17:47:50
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
gâtezu 78
La preuve pour 9 points elle utilise quoi comme arguments ?
Il y a sûrement plus simple.
#30 - 03-06-2014 19:00:48
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
GGâteau 78
Rien que de l'élémentaire avec quand même pas mal d'astuce ( on commence par enfermer les taches dans un triangle équilatéral orienté convenablement ) 
Six points c'est quand même autrement plus passionnant , je vais essayer de me renseigner .
Vasimolo
PS: j'avais aussi pensé au théorème de Helly mais je ne vois pas comment l'utiliser .
#31 - 05-06-2014 07:54:18
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,188E+3
gâtezu 78
Je vais essayer de faire simple :
Si on choisit un quadruplet de points, il est toujours possible de le regrouper en
4/0 3/1 ou 2/2, admettons qu'il soit recouvrable dans une de ces configurations.
La position de chacun des deux triangles est limitée par un ou deux points, éventuellement 3 mais cela revient à en prendre 2 dans la position limite du triangle vers le troisième..
Cela n'apporte aucune information déterminante sur la position éventuelle d'un cinquième point.
Par contre, si je choisis 5 points recouvrables,
Pour chaque quadruplet, j'ai la même situation qu'avant, mais je sais que chacun des cinquième points possibles est forcément inclus dans une des positions.
J'essaye alors d'imaginer qu'un point n'est pas recouvrable par les deux triangles.
La positon des deux triangles est donc limitée par d'autres points, et quels que soient ces points, ils se résument au maximum à 2 + 2 Donc , quel que soit la position des deux triangles permettant le recouvrement de tous les autres points, les quatre points limite et le point exclu implique que le quintuplet n'était pas recouvrable. CQFD
#32 - 08-06-2014 19:12:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#33 - 08-06-2014 20:41:31
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
gâtezu 78
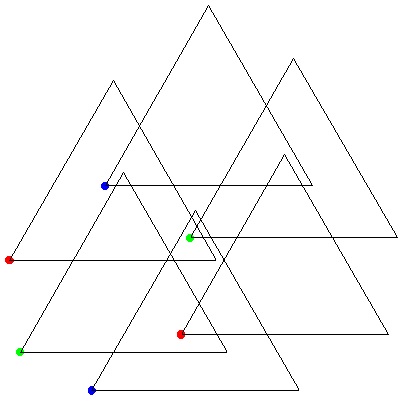
Comment recouvres-tu les deux points verts, les deux points rouges et le point bleu du haut ?
Il y a sûrement plus simple.
#34 - 08-06-2014 21:52:10
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
gâteai 78
Avec les 2 triangles rouge et vert de gauche.
#35 - 08-06-2014 22:10:40
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gtâeau 78
Non, ces triangles se superposent chevauchent. (Le pâtissier serait furax si on saccageait son travail en essayant de superposer chevaucher ces gâteaux  ) )
Il y a sûrement plus simple.
#36 - 09-06-2014 08:59:08
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteay 78
Je pense que le pâtissier acceptera que ses gâteaux se chevauchent légèrement 
Vasimolo
PS : J'ai modifié légèrement les positions des trois points du bas car ils tenaient dans un seul gâteau 
#37 - 09-06-2014 10:56:38
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gâteua 78
Comment ça légèrement ?
On a bien le même dessin sous les yeux ?
Le triangle avec le point rouge le plus à gauche et le triangle avec le point vert le plus à gauche se chevauchent plus que légèrement !
Un gâteau ce n'est pas comme une crêpe ou une galette, en général il y a une certaine différence entre le niveau de la table, et le dessus du gâteau. Faire chevaucher les deux gâteaux, ce ne serait pas beau et en plus ils risqueraient de se casser ! Et pour peu que le pâtissier ait fait quelques décorations, c'est foutu !
Plus sérieusement: on a le doit de chevaucher les gâteaux ou pas ?
C'est important, parce que sinon ce n'est plus le même problème.
En essayant de faire une preuve j'ai trouvé un contre exemple de 7 points dont on peut toujours recouvrir 6 d'entre eux sans pouvoir recouvrir les 7.
Mais ce n'est qu'un contre exemple uniquement dans le cas où l'on ne peut pas chevaucher les triangles ! Donc le chevauchement des triangles est un détail qui a son importance.
Il y a sûrement plus simple.
#38 - 09-06-2014 11:57:46
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâeau 78
D'accord avec Cogito: il s'agit de gâteaux, le recouvrement n'est pas autorisé, c'est du moins avec cette contrainte assez évidente que j'ai réfléchi au problème depuis le début.
Je crois que l'exemple de Vasi ne marche pas bien, il faudrait qu'il donne les 6 configurations pour être sûr.
#39 - 09-06-2014 12:01:26
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gtâeau 78
Disons que les gâteaux du pâtissier reposent sur des présentoirs permettant la superposition . L'objectif premier est de cacher les taches qu'on ne saurait voir .
Vasimolo
PS : Il vrai que le dessin initial laisse supposer que les gâteaux sont disjoints mais le problème me semble moins riche si on interdit la superposition . Tout ça peut bien sûr se discuter et/ou faire l'objet d'un nouveau gâteau 
#40 - 09-06-2014 13:26:34
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gâetau 78
Mais les présentoirs ils sont comment ? ils ont quels formes ?
peut-être qu'on ne verra pas les taches vu de dessus, mais avec une vue en biais on verra certaines tâches ?
Bon, je ne dis rien, parce que des énoncés foireux j'en ai fait aussi  , mais je pense que le fait de pouvoir superposer les gâteaux n'est pas quelques chose que l'on aurait pu imaginer, l'énoncé même suggère que l'on a cette contrainte de ne pas pouvoir le faire. Peut-être il aurait fallu dire que le pâtissier veux disposer des nappes triangulaire sur la table pour y poser son gâteau, et qu'il veut que les nappes recouvre toutes les tâches. Dans ce cas-ci, on aurait pu sérieusement envisager la superposition, mais là ... , mais je pense que le fait de pouvoir superposer les gâteaux n'est pas quelques chose que l'on aurait pu imaginer, l'énoncé même suggère que l'on a cette contrainte de ne pas pouvoir le faire. Peut-être il aurait fallu dire que le pâtissier veux disposer des nappes triangulaire sur la table pour y poser son gâteau, et qu'il veut que les nappes recouvre toutes les tâches. Dans ce cas-ci, on aurait pu sérieusement envisager la superposition, mais là ...
Sinon je ne vois pas trop en quoi le problème serait moins riche, la preuve, on arrive pas à trouver une démonstration, ni à déterminer le nombre de points minimum que l'on doit toujours recouvrir.
Disons que maintenant on a deux problèmes à résoudre un avec superposition et l'autre sans  . .
Bon je mets quand même mon contre exemple dans le cas où on ne peut pas superposer les triangles :
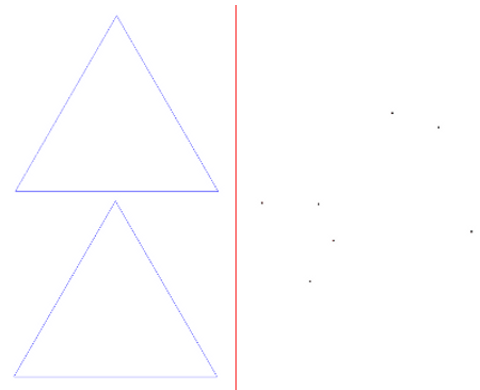

Il y a sûrement plus simple.
#41 - 09-06-2014 13:31:22
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
Gâteau 7
"PS : Ce gâteau est en fait un préambule à un 78 bis "un peu" plus compliqué."

Spoiler : [Afficher le message] Désolé mais mathématiquement je ne peux rien apporter, donc, je détends l'atmosphère ...
#42 - 09-06-2014 17:53:02
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#43 - 09-06-2014 18:41:36
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâeau 78
@Cogito
Ton contre-exemple pour sept points sans chevauchement à l'air de fonctionner mais c'est très pénible à vérifier ( je suppose que tu as fait tes dessins avec un logiciel de géométrie dynamique ) . En fait le problème est clairement discret et on doit pouvoir placer les points dans un "quadrillage" en triangles équilatéraux . On peut d'ailleurs le faire pour mon exemple précédent .
Vasimolo
#44 - 09-06-2014 23:29:30
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gâteau 7
En fait à priori, on aurait deux quadrillages, car le quadrillage obtenu à partir du premier triangle, et le quadrillage obtenu à partir du second ne coïncident pas forcément  . .
Mais effectivement, mettre un quadrillage permet d'avoir un support visuel pour mieux voir ce qui se passe.
Pour construire ce contre-exemple, je me suis dis que tracer le plus petit triangle équilatéral (bien orienté) qui contient tous les points pouvait aider.
Ensuite j'ai mis un gâteau dans un angle (ici en bas à droite) pour recouvrir deux points qui étaient sur les bords. Après je me suis dis que le point qui est sur le côté opposé du "grand triangle" devait être forcément recouvert par le deuxième gâteau. Ensuite j'ai regarder quels degrés de liberté j'avais. C'était le début de la preuve que je voulais faire, mais au lieu d'une preuve je suis tombé sur un contre-exemple  . .
Mais, mais mais,... ça voudrait dire aussi que si j'arrive à une telle configuration alors j'ai 7 points que je ne peux pas recouvrir  (comme c'est un pire cas, ça voudrait dire que sans chevauchement, c'est vrai à partir de 7). Mais bon ici encore il y aurait une longue analyse de cas, (mais pas forcément très compliqué je pense). (comme c'est un pire cas, ça voudrait dire que sans chevauchement, c'est vrai à partir de 7). Mais bon ici encore il y aurait une longue analyse de cas, (mais pas forcément très compliqué je pense).
EDIT : Quoique, ce n'est pas sûr  En faisant le même raisonnement avec les chevauchements, je trouve 5 points, ce qui est faux. En faisant le même raisonnement avec les chevauchements, je trouve 5 points, ce qui est faux. 
Il y a sûrement plus simple.
#45 - 10-06-2014 18:10:17
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteua 78
Oui Vasimolo, pour ton exemple à 6 pts sommets d'un hexagone (cas que j'avais bien sûr regardé), ça marche si superposition possible. Mais non si superposition interdite.
#46 - 11-06-2014 18:01:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteua 78
cogito a écrit:En fait à priori, on aurait deux quadrillages, car le quadrillage obtenu à partir du premier triangle, et le quadrillage obtenu à partir du second ne coïncident pas forcément  ./ ./
On a bien sûr un unique quadrillage à cause du nombre fini de points à recouvrir , par contre il faut faire varier le nombre de triangles constituant les gâteaux . La recherche d'exemples est bien plus simple car les sommets des gâteaux sont des nœuds du quadrillage .
Un exemple avec superposition interdite et sept points ( un gâteau = seize triangles )
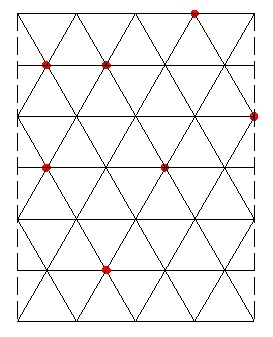
Vasimolo
#47 - 11-06-2014 23:16:40
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtteau 78
Un exemple avec huit points ( toujours en interdisant les chevauchements ) et des gâteaux formés de 5X5 triangles .
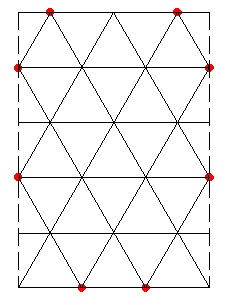
Il faut clairement chercher un maximum de symétrie dans les positions .
J'ai l'impression qu'on peut continuer comme ça à l'infini et que le pâtissier serait dans de mauvais drap s'il n'autorisait pas la superposition des gâteaux 
Vasimolo
#48 - 11-06-2014 23:27:48
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,188E+3
âGteau 78
Ca me rappelle un autre sujet actuel: c'est quoi l'énoncé correct et précis au bout du compte ? Parce que si je superpose mes gâteaux et que je passe dessus au rouleau compresseur, je recouvre tous les points que je veux  Il me semble que l'énoncé évolue au fur et à mesure des post alors je suis curieux de connaitre ta preuve à 9 points et ton idée initiale du problème. Il me semble que l'énoncé évolue au fur et à mesure des post alors je suis curieux de connaitre ta preuve à 9 points et ton idée initiale du problème.
#49 - 12-06-2014 00:31:16
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâeau 78
Un petit résumé du problème pour ceux qui n'ont pas tout suivi , c'est à dire tout le monde à une ou deux exceptions près 
Contrairement à mon habitude , je vais essayer d'être clair .
On a deux gâteaux en forme de triangles équilatéraux de même taille que l'on va disposer sur une nappe . L'orientation des gâteaux est imposée ( la même pour les deux ) mais pas la position .
Les deux gâteaux doivent cacher toutes les taches d'une nappe ( supposée infinie ) sur laquelle on les pose .
Hypothèse : On suppose que si on choisit "n" taches au hasard sur la nappe , on peut toujours les cacher avec les deux gâteaux .
Problème : comment choisir "n" minimum pour être assuré de pouvoir cacher l'ensemble des taches de la nappe ??????
1ère interprétation ( la mienne ) : pour cacher les taches on accepte que les gâteaux se superposent .
J'ai donné un exemple où n=5 taches quelconques peuvent être recouvertes mais pas la sixième . En bref n est supérieur à 5 mais combien vaut-il (s'il existe ) ?
2ème interprétation ( celle du reste du monde ) : On cache les taches sans superposer les gâteaux ) .
J'ai donné un exemple de n=7 taches quelconques peuvent être recouvertes par les deux gâteaux pas la huitième ( je pense qu'on peut aller bien plus loin ) .
J'espère que c'est plus clair
En tout cas , Gwen , quelle que soit ta compréhension du problème , ta solution n'est pas bonne 
Vasimolo
#50 - 12-06-2014 15:02:55
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
Gâteua 78
Dans l'exemple que tu donnes, les huit points sont recouvrables :
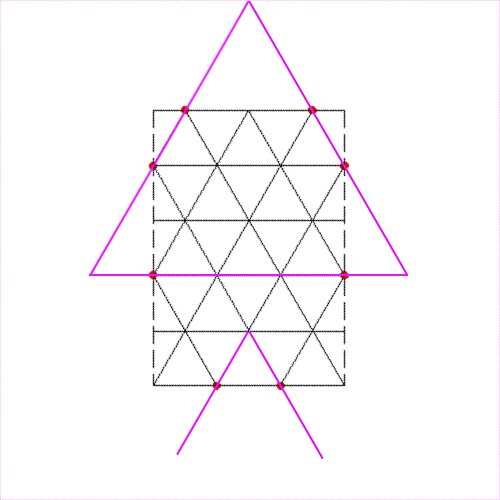
Il y a sûrement plus simple.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum