Enigme Gâteau 75 @ Prise2Tete

Vasimolo · #1

Mon pâtissier prépare Pacques assidument.

Avant cuisson, il range habituellement ses carrés de chocolat de taille $2\times 2$ sur une grille $20\times 20$ . Les sommets des carrés sont placés aux nœuds de la grille , les carrés peuvent être en contact mais ne se chevauchent jamais . Il a confectionné 48 carrés qu’il s’apprête à disposer sur la grille quand je lui propose d’ajouter un des miens . Comme il apprécie modérément mes dons culinaires ( et qu’il n’est pas toujours bon camarade ) il me dit qu’il doit d’abord disposer les siens et voir s’il reste une place .

Comment va-t-il faire pour m’empêcher de poser mon carré , si possible ?

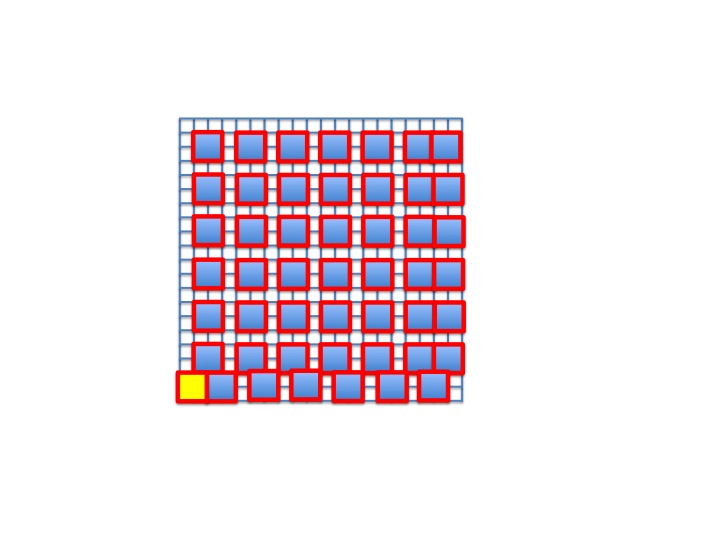
Un exemple sur une grille 8x8 qui empêche la pose d’un 10ème carré .

Amusez-vous bien

Vasimolo

gwen27 · #2

Comme ça dans une grille n x m avec ent [ (n+1)/3 ] x ent [ (m+1)/3 ] carrés.

cogito · #3

Bonsoir,

Au départ je me suis dit : "Non, il ne pourra jamais empêcher Vasimolo de rajouter son carré de chocolat."

Après je me suis rappelé : "C'est vrai qu'il est malin le bougre."
Ce n'est pas très sympa de sa part :

En même temps, il faut dire que ce qu'il fait est très joli

Vasimolo · #4

Je ne comprends rien aux deux réponses précédentes . La question n'est peut-être pas claire ?

Vasimolo

gwen27 · #5

C'est un cas général pour ma part...

Sur une grille 20x20 il peut s'il a 49 carrés en main.

Vasimolo · #6

Ta réponse n'est pas claire Gwen , le nombre que tu donnes est le nombre de carrés nécessaire pour bloquer la grille ?

Vasimolo

cogito · #7

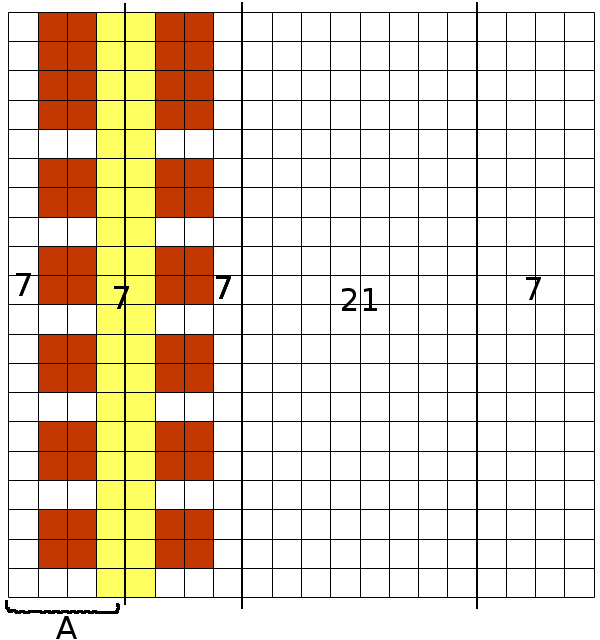
Le dessin représente la grille 20*20. Les cases marrons correspondent aux carrées de chocolats (Les carrés 4*4 sont 4 carré 2*2 côte à côte) il a donc poser 48 carrée 2*2 (il y en a 4 isolés dans chaque coins) et il n'y a pas la place pour un 49ème. c'était bien cela qui était demandé ?
J'aurais peut-être dû marquer les séparations entre deux carrés juxtaposés

Vasimolo · #8

@Cogito : il me semble que tu as posé bien plus de 48 carrés 2X2 , non ?

Vasimolo

gwen27 · #9

Oui

cogito · #10

huhum... oui effectivement, dans ma tête je me suis dis il y en a 4 * 16 et 4 * 16 ça fait 48 c'est bien connu !

Bon pardon, j'y retourne

Vasimolo · #11

@Gwen : alors c'est ça

Vasimolo

cogito · #12

Bonne nouvelle !

Tu pourras rajouter ton carré de chocolat !

Explication de ~~texte~~ dessin :

Dans une bande 20 * 4 (comme la colonne A) il sera toujours possible de mettre 7 carrés. Si on veut minimiser le nombre maximal de carrés que l'on peut mettre dans une bande 20 * 4, il faut que les carrés soient centrés (i.e. ne touche pas les bord de la bande sinon on pourrait mettre au même niveau un carré supplémentaire (puisque 4 = 2 * 2)).

Maintenant si on duplique la colonne A (qui contient le nombre de carré optimal)
pour optimiser le nombre de carrés dans une bande de largeurs 8, on s'aperçoit que les deux "bord" vide mis côte à côte créés un nouvel espace (en jaune) où nous pourrons toujours mettre 7 carrés. Si on décide de décaler un des 14 carrés
pour prendre la place d'un carré sur la bande jaune, alors d'après la dernière remarque du paragraphe précédent on aura créé la place pour un autre carré, donc le nombre de carrés total ne changerait pas. Tous ça pour dire que dans une bande de 20 * 8 on pourra toujours mettre 21 carrés.
(on ne pourra jamais en déplacer un pour prendre la place de 2 (ou alors si c'est le cas c'est qu'il est possible de mettre au moins huit carrés dans la colonne jaune donc au final, ça revient au même). Ce point de la démonstration est laissé en exercice pour le lecteur )

Donc dans une bande de 20 * 16 on pourra toujours mettre 42 carrés.
(on n'a pas ce "phénomène de la bande jaune" ici. Ce point est aussi laissé en exercice pour le lecteur )
Et donc si on ajoute les 7 carrés de la dernière bande de 4 on pourra toujours mettre 49 carrés 2*2 dans une grille de 20*20.

gnahaha !

titoufred · #13

On montre par récurrence sur n qu'une grille de dimensions (3n+2)x(3m+2) avec m $\leq$ n nécessite au moins (n+1)x(m+1) carrés pour être bloquée.

Initialisation : Pour n=0, donc m=0, on a une grille 2x2 qui nécessite 1 carré pour être bloquée.

Hérédité : On suppose que c'est vrai pour un certain n et on se donne une grille de (3n+5)x(3m+2) avec m $\leq$ n+1.

Si m $\leq$ n (grille non carrée), alors on coupe la grille en 2 grilles séparées d'une case (3n+2)x(3m+2) et 2x(3m+2) qui nécessitent chacune respectivement au moins (n+1)x(m+1) et (m+1) carrés soit au total (n+2)x(m+1) carrés. Le fait que les grilles soient séparées fait que les carrés de l'une ne peuvent aider à bloquer l'autre.

Si m=n+1 (grille carrée), alors on coupe en 4 grilles séparées d'une case : (3n+2)x(3n+2), 2x(3n+2), (3n+2)x2 et 2x2 qui nécessitent chacune respectivement au moins (n+1)x(n+1), (n+1), (n+1) et 1 carrés soit au total (n+2)x(n+2)=(n+2)x(m+1) carrés. Ce qui prouve l'hérédité.

dylasse · #14

Notre bon pâtissier ne pourra pas t'empêcher de placer ton chocolat. Et tu le sais puisque tu as colorié (dans ta tête) 49 blocs 2x2 sur la plaque. Ces 49 blocs présentent la particularité qu'aucun chocolat 2x2 ne peut en recouvrir simultanément 2, donc après que ton pâtissier aura déposé ses 48 chocolats, un bloc de 4 sera libre pour le tien.

Franky1103 · #15

Quand la grille carrée est du type 3n-2 < N =< 3n+1, en disposant n² carrés, on y arrive très facilement. Dans notre cas, il faudrait 49 (> 48) carrés. Il y a une astuce consistant à décaler les carrés, qui permet d'en économiser un, mais que je n'ai pas (encore) découverte. Affaire à suivre ...

Vasimolo · #16

Je vois qu'on a bien travaillé en mon absence

@Cogito : tu devrais pouvoir faire plus simple
@Titoufred : oui .
@Dylasse : parfait , très visuel et expéditif .
@Franky : à suivre ...

Bon courage à ceux qui cherchent encore .

Vasimolo

nobodydy · #17

arghhh je déteste ce genre de problème
J'ai l'impression que ce n'est pas possible, mais je ne peux pas le démontrer.

et si c'est possible de bloquer le gâteau jaune, ça m’énerve encore plus car je n'y arrive pas.

je pense que ce n'est pas possible, si je déplace un seul de mes gâteaux, il y aura toujours un espace pour le tien.

Est ce possible ?

Vasimolo · #18

@Nobodydy : ton intuition est bonne . Il y a des solutions très courtes , ce qui ne veut pas dire qu'elles sont faciles à trouver

Vasimolo

nodgim · #19

Salut Vasimolo,
En remplissant le casier comme un livre d'écriture, de gauche à droite et de haut en bas, en optimisant les espaces libres (1 unité systématique) on finit en bas en droite avec une agglomération de carrés sans espace libre. En ôtant le carré du coin, et en replaçant les carrés du pourtour on gagne ce vide.

Vasimolo · #20

Je ne crois pas Nogim

Vasimolo

Vasimolo · #21

J'avais une solution en numérotant les lignes de 0 à 20 et en remarquant que chaque ligne 1 ; 4 ; 7 ; 10; 13 ; 16 ; 19 devait rencontrer 7 gâteaux pour bloquer le jeu . Je préfère 100 fois celle de Dylasse qui démontre tout avec l'air de ne pas y toucher

Merci à tous pour la participation .

Vasimolo

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 15-04-2014 19:32:00

Gâtteau 75

#0 Pub

#2 - 15-04-2014 19:43:23

âteau 75

#3 - 15-04-2014 20:51:54

gâreau 75

#4 - 15-04-2014 21:23:07

âGteau 75

#5 - 15-04-2014 21:27:17

Gâtea 75

#6 - 15-04-2014 21:32:52

gâtezu 75

#7 - 15-04-2014 21:34:56

Gâteua 75

#8 - 15-04-2014 21:38:30

Gâtea 75

#9 - 15-04-2014 21:39:28

âteau 75

#10 - 15-04-2014 21:42:47

gâteay 75

#11 - 15-04-2014 21:46:34

Gâteau 775

#12 - 16-04-2014 00:02:23

Gâteau 7

#13 - 16-04-2014 01:02:32

Gtâeau 75

#14 - 16-04-2014 10:27:01

Gâteeau 75

#15 - 16-04-2014 15:54:47

Gâteau 755

#16 - 16-04-2014 17:38:47

Gâeau 75

#17 - 17-04-2014 13:45:47

Gâteau 7

#18 - 17-04-2014 18:00:11

âteau 75

#19 - 18-04-2014 07:19:24

gâteay 75

#20 - 18-04-2014 08:54:03

hâteau 75

#21 - 19-04-2014 12:46:47

gâreau 75

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums