Belle réponse ! Sauf qu'en maths, "ça dépend" est un synonyme de "non"

Une chance sur deux : je réponds "oui". Comme ça, pour le sport.

Je pense que c'est vrai et même d'une infinité de manières.
En prenant un point O assez central à l'intérieur du quadrilatère ABCD, on pourrait le relier à des points E, F, G et H appartenant chacun à un côté.
Il resterait à ajuster la position de ces points sur ces segments pour que les quatre aires soient égales.
Quel point O donnerait l'approche la plus sympathique... le centre de gravité de ABCD ?

Le problème n'est pas sans rappeler celui-ci :

http://www.diophante.fr/D4.-Pavage-du-plan-et-de-l-espace-Dissection/D462.-Le-triangle-se-met-en-quatre.html a écrit:

De combien de façons peut on découper un triangle scalène en quatre triangles de même aire ?
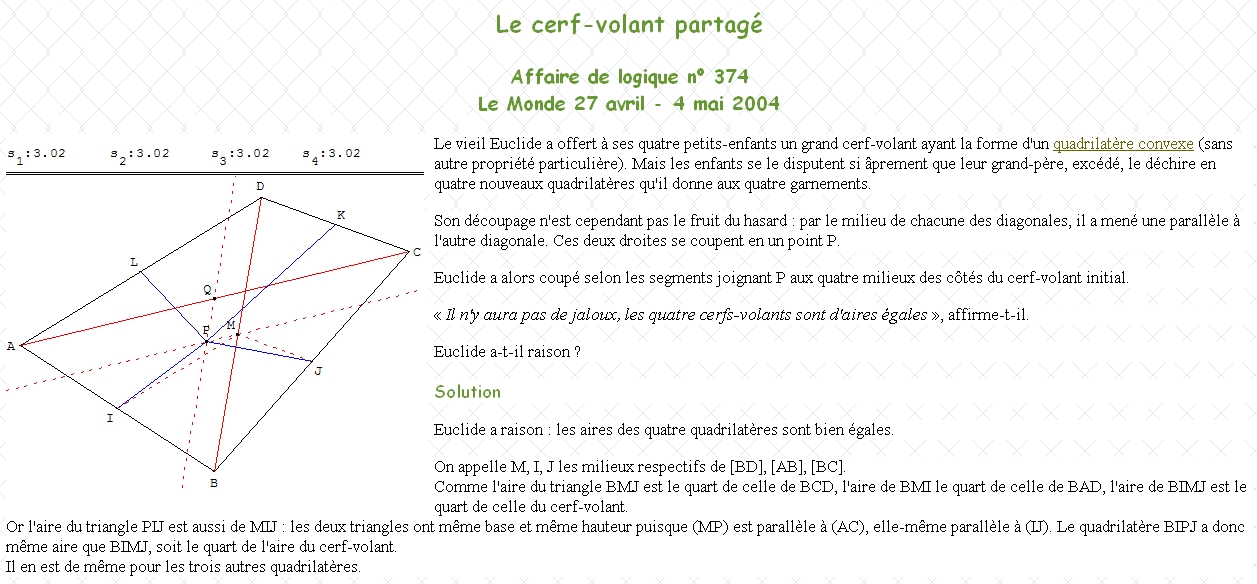
XX, YY et ZZ ont dénombré 108 découpages possibles. On peut raisonnablement conjecturer que c'est le nombre maximum de découpages possibles.

Soit ABCD un quadrilatère convexe et I milieu de [AB]; J milieu de [BC]; (d1)la droite parallèle à (AD) passant par I et (d2) la droite parallèle à (CD) passant par J et K la point d'intersection des deux droites. Alors le quadrilatère IBJK est une réduction de ABCD par 2 et donc l'aire est divisée par 4.

Maintenant il faut placer E sur [AD] pour que le trapèze IAEK soit égal à l'aire du quadrilatère IBJK et F sur [CD] pour que le trapèze JCFK soit égal à l'aire du quadrilatère IBJK

je poursuivrai plus tard

Joli scrablor !!!



Vasimolo

J'aurais aussi aimé trouver cette solution par moi-même !
Je pense qu'on peut y parvenir en commençant par le milieu M de la diagonale [AC] qui permet de délimiter deux domaines d'aire voulue puisqu'ils sont homothétiques de ABCD dans le rapport 1/2.
En général, les deux autres secteurs ne sont pas de même aire. Il suffit alors de « déplacer » le point M parallèlement à l'autre diagonale...

Bonjour !

Mon ami GETA pour GATO6 m'avait conduit à cette page
http://pagesperso-orange.fr/debart/geop … html#af374



qui revient à la construction trouvée par Scrablor ....

Merci à Vasimolo d'avoir rebondi sur le sujet (boiing! boiing !)

A bientôt,