Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 31-10-2015 17:58:01
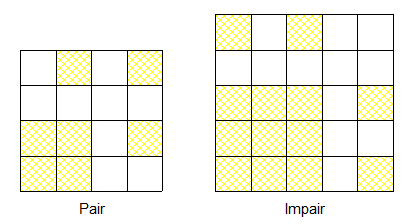
Optimisation de caarrésBonjour Un promath- actif dans un forum actif
#0 Pub#2 - 31-10-2015 18:45:03#3 - 31-10-2015 19:01:25#4 - 31-10-2015 19:08:39#5 - 31-10-2015 23:55:45
Optimisation e carrésÇa semble trop simple : j’ai dû rater quelque chose. #6 - 01-11-2015 08:04:14
Opitmisation de carrésSalut Promath, #7 - 01-11-2015 08:49:38#8 - 01-11-2015 09:31:48
optimisarion de carrés1 #9 - 01-11-2015 10:57:09#10 - 01-11-2015 11:51:13
Otimisation de carrésBonjour, #11 - 28-11-2015 17:05:44
OOptimisation de carrésBien! Un promath- actif dans un forum actif Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | |||||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.