Bonsoir,
Sauf erreur de calcul, je trouve que le tunnel a une longueur de 960 m, ses extrémités sont respectivement à 4,8 km et 12 km de Sainte Anne et Saint Brice, et les vitesses respectives de Marie et Jean sont de 14,4 km/h et 18 km/h.

L1 = distance de Saint Brice à l’entrée du tunnel
L2 = distance de Saint Anne à l’autre entrée du tunnel
Lt = longueur du tunnel
V1 = vitesse de Jean
V2 = vitesse de Marie

Pas facile d’écrire des équations sans latex
L1/V1 = L2/V2 + 1/3 (équation n°1)
Lt/0,8V1 = L2/0,8V1 - 1/60 (équation n°2) => Lt = V1.V2 / 75(V1-V2)
-1/3 + L1/V1 + Lt/0,8V1 + L2/V1 + 1/3 = L2/V2 + Lt/0,8V2 + L1/V2 - 1/4
=> 7/30 + L2/V1 = L1/V2 (équation n°3)
-1/3 + L1/V1 + Lt/0,8V1 + L2/V1 + 1/3 + L2/V1 + Lt/0,8V1 + 6/V1 = L2/V2 + Lt/0,8V2 + L1/V2 + L1/V2 - 6/V2
=> L2/V1 + Lt/0,8V1 + 6/V1 = 1/4 + L1/V2 - 6/V2 (équation n°4)
2L2/V2 + 2Lt/0,8V2 + 2L1/V2 + 2/4 = 3
=> L2/V2 + Lt/0,8V2 + L1/V2 = 5/4 (équation n°5)

J’ai donc 5 équations et 5 inconnues: à priori je devrais m’en sortir, sauf que les équations sont inextricables.
Affaire à suivre …

salut.

@ nodgim :
oui c'est une énigme que j'ai conçue comme quelques unes précédentes . honnêtement , je ne pensais pas qu'elle aurait fait reculer la plupart des
matheux et logiciens du forum. j'ai trouvé deux méthodes pour la résoudre.
1) avec une simple équation niveau bon collégien.
2) avec l'observation

énigmatus , que j'applaudis en passant , est le seul à avoir donné la bonne réponse
et la seule réponse d'ailleurs .
@énigmatus , j'aurais bien aimé voir ta résolution .

bonsoir.

et merci aux participants . Je propose deux types de résolutions
avec rien d'inextricable et d'indigeste .

Solution avec 2 méthodes  .

première méthode:   (avec une équation)
je pose avant toutes les inconnues. 

x  est la longueur du tunnel
a  est la distance entre saint-anne et le tunnel
b  est la distance entre saint-brice et le tunnel
d = a + b + x  est la distance séparant les 2 villages.
vm  la vitesse de marie dans le tunnel  ,  vj  , celle de jean dans le tunnel .
Vm  la vitesse de marie au grand jour et Vj  , celle de jean au grand jour.

A la lecture du texte , on constate que marie a effectué sa balade en 3 heures ,
mais comme elle a marqué 2 temps d'arrêt d'un quart d'heure , elle a donc roulé
durant 2h30min. Elle effectue donc une traversée en 1h15min.

A 10h15 , elle est arrivée à saint brice. Jean a quitté saint anne un quart d'heure
plus tôt après 20min de pose.

Il a donc effectué sa traversée en 1h . Par conséquent :

a)   les vitesses étant constantes et dans le tunnel et au grand jour , le rapport
des vitesses est :
[TeX]  \frac{Vj}{Vm} = k = 1.25[/TeX]
b) ils rentrent la première fois en même temps  dans le tunnel , mais marie y reste
1min de plus ; alors on peut conclure avec k=1.25 que jean le traverse en 4 min  et
marie en 5 min.

    les vitesses en sont déduites
[TeX] \begin{cases}v_m&=12x\\v_j&=15x\\V_m&=15x\\V_j&=18.75x\end{cases}[/TeX]
vitesses exprimées en km/h

c)  calcul de a , b et d 

    Jean parcours  a + b + x  en 1h  , mais il parcours x en 4 min. Il parcours donc  a + b  en 56 min. Mais sa vitesse sur a et b    étant de 18.75x km/h , alors:
[TeX]  a + b = 18.75x \times{\frac{56}{60}} = 17.5x[/TeX]
  on en déduit d :           d = 17.5x + x = 18.5x km

   Jean est parti 20 min avant marie , et il a déjà parcouru :
[TeX] L = 18.75x \times{\frac{20}{60}} = 6.25x (1)[/TeX]
   à 9h il leur reste donc à parcourir ensemble 11.25x km avant d'arriver aux entrées du tunnel. On en déduit a et b
[TeX] a = 11.25x \times{\frac{1}{1+k}} = 11.25x \times{\frac49} = 5x [/TeX]
   et [latex] b = 18.5x - 5x - x = 12.5x [/latex]

  ce qu'on connaît maintenant.

Les vitesses en km/h
[TeX]\begin{cases}v_m&=12x\\v_j&=15x\\V_m&=15x\\V_j&=18.75x\end{cases}[/TeX]
Les distances en km
[TeX]\begin{cases}a&=5x\\b&=12.5x\\d&=18.5x\end{cases}[/TeX]
      on s'occupe seulement du retour des tourtereaux.

    A 10h15 , lorsque marie démarre de saint-brice , jean a  déjà quitté saint-anne  depuis  un quart d'heure.  Marie va parcourir  (12.5x - 6) km à grande vitesse .
Jean va parcourir  (5x + 6) à grande vitesse  et  x à petite vitesse.  d'où l'équation de temps:

"t" (exprimé en heure) étant le temps écoulé entre 10h , heure de départ de jean et l'heure de rencontre.
[TeX] t = \frac14 + \frac{12.5x - 6}{15x} = \frac{5x + 6}{18.75x} + \frac{x}{15x}[/TeX]
donne après toutes les simplifications :  75x = 72   donc x = 0.96 km

t = 0h 40 min ;  la rencontre est effectuée à 10h 40min.  On calcule toutes les inconnues

pour vérifier par la suite.
[TeX]\begin{cases}v_m&=11.52km/h\\v_j&=14.4km/h\\V_m&=14.4km/h\\V_j&=18km/h\end{cases}[/TeX][TeX]\begin{cases}a&=4.8km\\b&=12km\\d&=17.76km\end{cases}[/TeX]
_ seconde méthode: (basée sur l'observation)



1) l'épisode de la première traversée du tunnel. Comme ci-dessus on en tire les 4 vitesses.

2) le décalage de 20min.

     On peut remarquer que jean part à 8h 40  , 20 min  avant marie et fait une pause de même durée ( 20 min).

  Cela signifie que si les 2 tourtereaux s'envole à 9h , si jean ne fait pas sa pause , alors le lieu  et l'heure de rencontre restent inchangés.

3) les distances cumulées.

     On remarque aussi que dans ce cas , s'ils partent tous les deux à 9h , en 1 h15  (à 10h15)  ils ont parcouru  9/4 de d (d = distance séparant les 2 villages)
On s'aperçoit aussi qu'au moment de la rencontre sur le chemin du retour ils ont parcouru  à eux deux 3d .

Ainsi l'heure de rencontre s'effectue à :
[TeX]  9h + 1h 15min \times{\frac43} = 10h 40min[/TeX]
soit 25 min après que marie soit partie de saint-brice .

4) le rapport des vitesses (k) est l'inverse du rapport des temps : (1/k)

  On sait aussi que marie parcourt en 25 min la même distance que jean en 20 min. Et c'est la  distance qu'il avait parcourue à 9h . A 9h Jean se trouve donc au panneau indiquant les 6 km .
Et à ce moment là marie quitte sainte-anne  , comme ils vont se retrouver en même temps  aux entrées du tunnel , on en conclut que :
[TeX] \frac{6}{a} = k = 1.25 [/TeX]
on en déduit  a = 4.8 km  . Maintenant , sur le chemin du retour , à partir de 10h 40 ,  marie et jean se retrouvent à 6+4.8+x km de st-anne soit (10.8 + x) km   dont x (le tunnel) sont parcourus en 5min par marie et 10.8 sont parcourus en  45min. par marie
(1h15min - 0h25min - 0h5min)

sur ce tronçon de 10.8km marie roule à grande vitesse : 15x km/h  . Si elle zappe
ses 2 quarts d'heure de pause :

Alors:
[TeX]  15x = 10.8\times{\frac{60}{45}} = 14.4 [/TeX]
   alors  x = 0.96 km . Et le raisonnement eût été le même si on avait travaillé avec jean  sur l'aller . il lui serait resté 10.8 km à parcourir   en 36 min
36 = ( 60 - 20 - 4)  à la vitesse de 18.75 km/h
[TeX]  18.75x = 10.8\times{\frac{60}{36}} = 18 [/TeX]

J'arrive un peu après la bagarre

Je n’ai pas trouvé le temps de chercher sérieusement le problème avant la solution mais comme j’avais trouvé le problème intéressant , j’ai continué à chercher sans regarder les réponses .

Il faut vite évacuer les parasites du problème : divers arrêts et ralentissements . On peut supposer que les deux tourtereaux ne font pas d’arrêt et qu’ils roulent à vitesse constante ( en réduisant de 20% les longueurs hors tunnel ) . On peut noter 15 la distance entre les deux villes ( ce n’est pas gênant ,15 quoi ? ) .



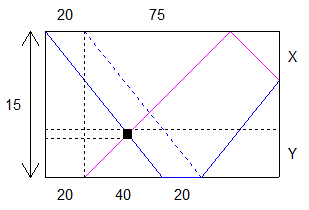
Marie fait l’aller et retour en 150 minutes donc un aller simple en 75 minutes et il faut 60 minutes à Jean pour faire la même chose . Plus simplement , Marie se déplace de 1 en 5 minutes et Jean en 4 minutes . Or dans le tunnel Jean a pris une minute à Marie , le tunnel fait donc 1 . Maintenant , si on déplie les trajectoires bleues et roses on voit qu’avant de se retrouver Jean et Marie vont parcourir 45 à eux deux . Or ils parcourent 0,45 par minute , ils vont donc se rejoindre après 100 minutes ( en considérant qu’ils partent en même temps et qu’ils ne font pas de pose ) .  Mais durant ces 100 minutes Marie a parcouru 15 + X = 20 donc X = 5 .

Il reste maintenant à regarder ce qui se passe au premier passage du tunnel .



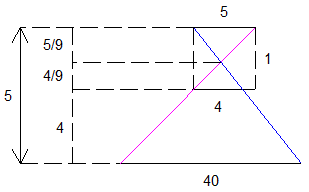
Les trois triangles semblables nous donnent  Y = 5 et on arrive au schéma complet :



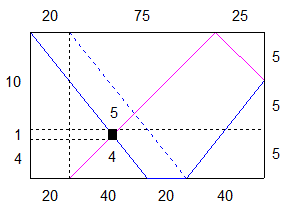
Le panneau affichant la position du tunnel 6km nous indique que 4,8 km correspondent à 5 du dessin , le tunnel fait donc 4,8/5 = 0,96 km .

Merci pour ce joli problème

Vasimolo