 |
#1 - 13-03-2016 23:46:42
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
jean-claude, l'aveille mathématicienne
Oyez, oyez, la mystérieuse histoire de Jean-Claude, l'abeille mathématicienne.
Jean-Claude l'abeille doit se rendre à une alvéole afin de nourrir une larve. Il se déplace d'alvéole en alvéole. La distance entre deux alvéoles est, par définition, la distance entre leurs deux centres, et on pose à 1 la distance entre deux alvéoles qui se touchent.
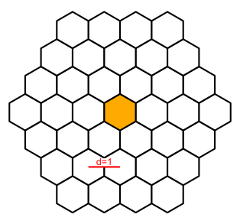
D'un côté, Jean-Claude souhaite prendre le maximum de temps possible pour effectuer sa tâche, afin de réfléchir en chemin à la démonstration de la conjecture de Riemann. D'un autre côté, il doit prendre garde à ne pas être identifié comme un tire-au-flanc, sinon il risque de se retrouver affecté à la surveillance de la ruche face à vespa velutina, activité périlleuse si elle en est.
Jean-Claude décide ainsi de se fier aux deux règles suivantes :
* règle 1 (prudence) : à chaque déplacement, il se rapproche strictement de son but, pour ne pas se faire repérer.
* règle 2 (nonchalance) : il emprunte un trajet le plus long possible pour rejoindre son but.
On sait de plus que la trajectoire empruntée ne comporte pas d'angle aigu (sur la figure ci-dessous, la trajectoire de droite comporte un angle aigu, pas celle de gauche), et qu'initialement, la distance entre Jean-Claude et la larve est un nombre premier.
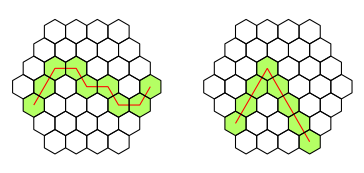
Pouvez-vous déterminer quelle est la longueur du plus grand trajet qui vérifie les conditions de l'énoncé ?
Indice 1 :
Spoiler : [Afficher le message] Il peut être utile de calculer les distances des cellules de la ruche à la larve. L'image ci-dessous donne les carrés de ces distances :
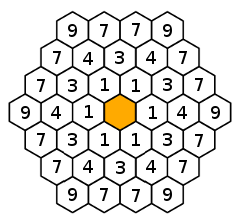
Indice 2 :
Spoiler : [Afficher le message] Si Jean-Claude est placé initialement dans une cellule à la distance 3 de la larve (donc numérotée 9 dans le dessin de l'indice 1), l'application des règles 1 et 2 implique qu'il va suivre le chemin 9-7-4-3-1-0 (chemin de longueur 5).
Or un tel chemin comporte forcément au moins un angle aigu (9-7-4). On en déduit que Jean-Claude n'est initialement pas placé sur cette cellule.
Indice 3 :
Spoiler : [Afficher le message]
S'il respecte les deux règles, et si sa trajectoire ne comporte pas d'angle aigu, alors Jean-Claude emprunte une des spirales rouges et vertes :
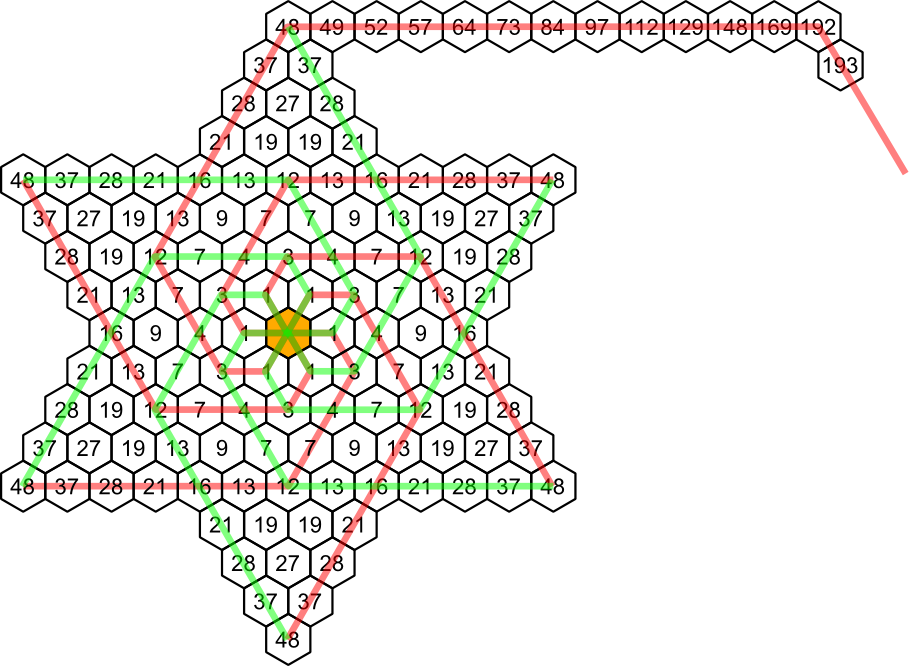
#2 - 14-03-2016 11:11:54
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Jean-Claude, l'abeille mathématicinene
L'énoncé est hautement ambigu !
Point de départ ?
Point d'arrivée ?
But ?
De toute façon à chaque déplacement on se rapproche strictement de la position finale...
#3 - 14-03-2016 13:29:23
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Jean-Claue, l'abeille mathématicienne
@masab : je ne pense pas avoir oublié de données, normalement, on peut résoudre le problème avec juste ces informations.
Le point d'arrivée est une certaine cellule de la ruche (la ruche est de taille potentiellement infinie). Mais le point de départ, on ne le connaît pas. Avec les informations de l'énoncé, seules certaines cellules sont des points de départs possibles, et on recherche celle qui correspond au plus long trajet.
Je donnerai un indice un peu plus tard si nécessaire.
#4 - 14-03-2016 18:28:55
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
jean-claude, l'abeimle mathématicienne
Il y a un problème avec les distances entières.
Pour d=7, par exemple, on peut l'avoir par une ligne qui est dans l'alignement des cotés (cas général) mais aussi par une ligne qui n'est pas en alignement avec les cotés (7= 3 + 5 dévié à 120°). Dans ce cas de figure, on obtient 11 sauts pour le 1er cas, et 10 pour le second.
#5 - 14-03-2016 21:50:22
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Jean-Claude, l'abeille mtahématicienne
Salut !
Je ne comprends pas bien non plus : Si la ruche est infinie, le chemin ne l'est-il pas lui même ?
#6 - 14-03-2016 22:18:26
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Jan-Claude, l'abeille mathématicienne
@nodgim : il y a quelque chose que tu n'as pas compris comme il faut, mais il est vrai que ce point de l'énoncé est retors.
Pour choisir son chemin, Jean-Claude ne respecte que les règles 1 et 2. A posteriori, on constate que le chemin qu'il a choisi a la propriété de n'avoir pas d'angle aigu.
Par exemple, imaginons que Jean-Claude soit au départ sur une cellule à distance 3 de la larve. Alors, les chemins respectant les règles 1 et 2 sont de longueur 5, mais tous ces chemins ont un angle aigu. On en déduit qu'au départ, Jean-Claude n'est pas à distance 3 de la larve.
@golgot59 : la réponse que je donne à nodgim ci-dessus élimine certaines cellules, qui ne peuvent être le point de départ de Jean-Claude. Comme on sait de plus que la distance entre le point de départ et la larve est un nombre premier, ça en élimine encore plus... En restera-t-il une infinité à la fin ? À voir...
#7 - 15-03-2016 08:12:24
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Jean-Claude, l'abielle mathématicienne
Quand tu dis que la distance du point de départ est un entier premier, c'est à vol d'abeille ?
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#8 - 15-03-2016 08:25:31
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Jean-Claude, l'abeille mathématiicenne
@fix33 : oui, quand je dis que la distance à la larve est un nombre premier, il faut comprendre la distance en ligne droite.
#9 - 15-03-2016 09:06:49
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Jean-Claude, l'abeille mathématicinene
@ Ebichu: je crois que tu n'as pas bien compris ce que j'ai écrit. Je t'indique qu'il y a un problème dans l'énoncé. Il s'agit de la contrainte: l'abeille est à une distance entière de l'objectif. Cette distance entière se trouve évidemment tjs en comptant les alvéoles parallélement à une des 3 directions de l'hexagone, mais aussi parfois sans suivre l'une de ces directions. Et je dis que dans ce cas on ne tombe pas sur le même résultat. Car on ne part du même point de départ.
J'ai bien compris la contrainte pas d'angle aigu, et en gros le trajet doit tourner autour de l'objectif par des segments qui suivent l'une des 3 directions. Reste à quantifier la longueur de cette spirale.
#10 - 15-03-2016 09:19:48
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
jean-claude, m'abeille mathématicienne
@nodgim : il n'y a pas de problème dans l'énoncé, ou alors, pas ici  Car dans l'exemple dont tu parles dans ton message #4, il y a un des deux cas qui ne peut pas être la cellule de départ de Jean-Claude, pour la même raison qu'une cellule à la distance 3 de la larve dont je parle dans mon message #6. Ce qui lève l'ambiguïté. Car dans l'exemple dont tu parles dans ton message #4, il y a un des deux cas qui ne peut pas être la cellule de départ de Jean-Claude, pour la même raison qu'une cellule à la distance 3 de la larve dont je parle dans mon message #6. Ce qui lève l'ambiguïté.
#11 - 15-03-2016 09:57:11
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Jean-Claude, l'abeille athématicienne
"et qu'initialement, la distance entre Jean-Claude et la larve est un nombre premier".
Alors c'est que je n'ai pas compris cette phrase dans le contexte de cette enigme. Pour moi, il s'agit d'une ligne droite à vol d'oiseau. Non ?
#12 - 15-03-2016 10:10:25
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
jean-claude, l'abeille mathématicirnne
Pour moi, une cellule à la distance 3 donne un chemin de longueur 4. Pourquoi y a t'il un empêchement pour cette distance ?
#13 - 15-03-2016 10:43:08
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Jean-Claude, l'abeillee mathématicienne
@nodgim : la distance est bien une ligne droite à vol d'oiseau. Et la longueur est 5, pas 4, car il faut respecter la règle 2.
#14 - 15-03-2016 10:55:51
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Jean-Claude, l'abeille mahématicienne
Dessine nous le trajet pour d=3 car je ne vois pas en 5 coups. ça n'entamera pas l'enigme je crois, qui me semble assez raide pour la généralité.
Sinon, 4 ou 5, pourquoi dis tu que d=3 au départ n'est pas possible ?
#15 - 15-03-2016 11:05:48
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Jean-Claude, l'abeille mathéématicienne
@nodgim : je ferai un dessin ce soir (là je ne peux pas) et je le placerai en indice. Avec le dessin, ce qui te pose problème devrait s'éclairer.
#16 - 15-03-2016 11:35:23
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
jzan-claude, l'abeille mathématicienne
J'ai compris Ebichu, mais il m'a fallu du temps....
L'angle aigu n'est pas une contrainte, mais si le chemin le plus long n'a pas d'angle aigu, alors il est correct.
#17 - 15-03-2016 19:26:40
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Jean-Claude, l'abeille mathématticienne
J'ai rajouté 2 indices.
@nodgim : c'est ça.
#18 - 16-03-2016 09:53:51
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Jean-Claude, l'abeille mathméaticienne
Il manque une précision dans la règle 2 :
règle 2 (nonchalance) : il emprunte un trajet repectant la règle 1 et le plus long possible pour rejoindre son but.
#19 - 16-03-2016 13:42:02
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
jean-claude, l'abeille matjématicienne
@masab : ce que tu dis est vrai. Mais autrement, le problème n'aurait pas de sens... Et quiconque a déjà glandé au travail sait que le plus important est de ne pas se faire attraper 
#20 - 16-03-2016 19:04:59
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
jean-claude, l'abeille mathématiciebne
Je suis perplexe.
En raisonnant à l'envers :
Une "spirale" permet de s'éloigner en permanence d'un point donné
sans faire d'angles aigus.
Les deux règles sont donc respectées.
Il existe dans le plan de grandes quantités de distances entières et premières
entre les centres des hexagones, même hors la ligne droite, solution triviale.
(avec un tableur, j'en ai identifié quelques-unes,
7,11,13,17,19,23, 29, 31)
J'ai donc un doute sur l'unicité de la solution.
J'attends les réponses avec une certaine curiosité.
#21 - 16-03-2016 19:25:09
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Jean-Claude, l'abille mathématicienne
@halloduda : l'indice 2 permet d'éliminer le nombre premier 3. De même, certains de ta liste peuvent être éliminés.
#22 - 16-03-2016 19:39:17
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Jean-Claude, l'abeille athématicienne
Il y a quelque chose de remarquable dans cette énigme.
Si on dessine 3 axes concourants avec angle 60°, que le centre est l'objectif, et que d'un pt quelconque on veuille rejoindre le centre en suivant les axes, mais sans jamais se diriger directement vers le centre, tout en se rapprochant strictement, alors tous les chemins possibles ont la même longueur (pas en discret, mais en continu), angles aigus ou pas. Du coup, ce n'est plus la distance de l'objectif qui peut faire la différence, mais bien le mode discret, selon que l'on peut atteindre ou pas une case alignée par un des 3 axes avec la case centrale. Evidemment, le fait de pouvoir se servir des angles aigus donne plus de marge, et donc la possibilité de tracer un trajet plus long.
Je n'ai pas encore compris vraiment d'où pouvait venir cet écart. Ou si c'est systématique.
#23 - 16-03-2016 22:26:59
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Jean-Claude, l'abeille mathémtaicienne
@nodgim : tu es sur la bonne voie.
#24 - 17-03-2016 19:49:37
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Jean-Calude, l'abeille mathématicienne
En réalité, il faut, pour empêcher qu'un chemin à angle aigu plus long existe, que chaque segment tracé finisse juste sur une case alignée avec l'un des 3 axes perpendiculaires aux 3 axes des cotés. Si cette condition n'est pas respectée, on peut ajouter une cellule (à angle aigu) sur ce segment en le déformant légèrement.
En pratique, pour éviter cet inconvénient, on trouve que la distance de cette case à la case objectif doit être de la forme (2^n) * V3. Et pour que la distance d entre la case origine et la case finale soit un entier, il faut et il suffit que cette distance obéisse à la règle de Pythagore: d² = a² + (2^n*V3)². Pour répondre à la question, il faut en plus que d soit premier.
Comme (2^nV3)² est une différence de 2 carrés, qu'on sait qu'entre 2 carrés consécutifs, la différence est impaire et linéaire, on peut déduire facilement la forme de d impair:
d = 3*4^n + 1 ou d = 4^n + 3.
qui donne 2 formes de triangles rectangles à coté entiers impairs pour les 2 plus grands:
-( 3 * 4^(n-1) -1 ; 3 * 4^(n-1) + 1 ; V3 * 2^n )
-( 2^(2n-2) + 3 ; 2^(2n-2) - 3 ; V3 * 2^n )
On a plein de solutions particulières de la forme d =3*4^n + 1 premier (13, 193, 769,.196609...) ou 4^n + 3 (7,19,67,4099,65539,...)
On peut raisonnablement penser qu'il n'y a pas de dernier nombre premier de l'une ou l'autre des formes de d.
#25 - 17-03-2016 22:08:17
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Jean-Claude, l'abeille mathématiicenne
@nodgim : je suis d'accord avec la relation que tu obtiens à la fin du premier paragraphe ; attention toutefois, elle est nécessaire, mais pas suffisante, car elle ne tient pas compte de ce que tu expliques par "chaque segment tracé finisse juste sur une case alignée avec l'un des 3 axes perpendiculaires aux 3 axes des cotés".
C'est-à-dire que dans ta relation, "a" doit être bornée. Du coup, 193, par exemple, ne marche pas.
Tu y es presque, il n'y a plus que ce problème à régler, et on saura enfin quoi faire de ce Jean-Claude 
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum










