Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 15-05-2017 18:09:31
tous xhez le maire !Bonjour à tous
#0 Pub#2 - 15-05-2017 21:49:05
tous cgez le maire !ca m'a l'air difficile, la complexité du calcul semble augmenter à chaque villageois rajouté. #3 - 15-05-2017 22:24:57#4 - 15-05-2017 22:42:26#5 - 15-05-2017 22:52:51#6 - 15-05-2017 23:23:36#7 - 16-05-2017 08:25:33#8 - 16-05-2017 09:36:48#9 - 16-05-2017 17:10:56
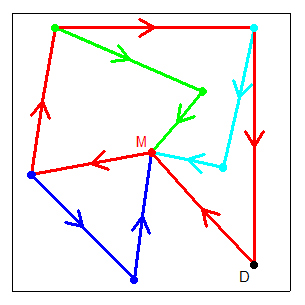
rous chez le maire !Je suis d'accord avec cette limite qui est clairement indépassable ( par en dessous ) car en disposant tous les villageois dans deux coins opposés on atteint les [latex]2\sqrt{2}[/latex] . Maintenant j'ai l'impression qu'on doit atteindre la limite assez vite ( avec une poignée d'habitants ) mais je n'ai pas d'argument . Réponse rapideSujets similaires
|
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.