Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 06-12-2017 22:20:06
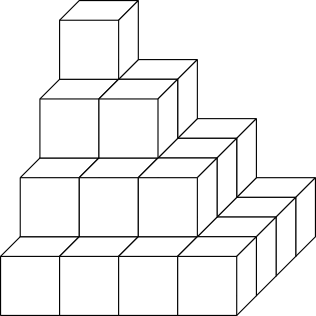
Thiking inside the boxBonjour à tous,
#0 Pub#2 - 07-12-2017 14:33:39
Thinking inisde the boxBonjour? #3 - 07-12-2017 18:05:33#4 - 11-12-2017 19:54:27
thinking unside the boxMerci à leresolus pour sa participation, ainsi que sa solution très visuelle. Réponse rapideSujets similaires
|
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.