 |
#1 - 20-04-2018 19:18:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Eches 23
Bonjour à tous .
J'ai un peu honteusement laisser tomber les grilles , dés , cartes , tours de magie , jeux à 2 depuis un moment au profit de gâteaux de plus en plus indigestes .
Je vais essayer de me faire pardonner avec quelques petits problèmes plus ou moins originaux et plus ou moins faciles .
On pose 16 pions d'Othello ( un côté blanc et un côté noir ) sur une grille carrée 4 X 4 . Au départ tous les pions exposent leur face blanche mais on peut les retourner de la façon suivante : on choisit une case, puis on retourne le pion de cette case ainsi que ceux de toutes les voisines ( partageant un côté avec celle-ci ) .
Cette manipulation constitue "un coup" .
Le résultat obtenu en 3 coups en choisissant les cases ornées d'une croix rouge :
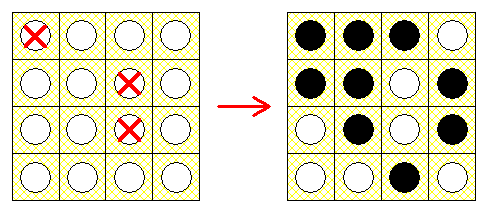
On peut chercher le minimum de coups pour noircir le tableau ( facile ) mais aussi chercher de façon exhaustive le nombre de coups autorisés ou interdits pour noircir le tableau ( un peu moins facile ) .
Amusez-vous bien 
Vasimolo
#2 - 20-04-2018 19:32:32
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
ecjecs 23
en 3 coups, ça me semble jouable
OOOO
OOOX
OOOX
XOOO
#3 - 20-04-2018 19:36:53
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#4 - 20-04-2018 21:55:43
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,177E+3
Ecchecs 23
Le minimum est 4 et il n'y a que 16 solutions. 
#5 - 20-04-2018 22:03:46
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Echeecs 23
C'est bon pour le minimum Gwen 
Il y a mésentente sur la deuxième partie de la question , on retourne le jeu en "n" coups , donner toutes les valeurs possibles de "n" .
Vasimolo
#6 - 20-04-2018 22:14:28
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,177E+3
echevs 23
OK, parce qu'il ne peut y avoir que 16 solution vu que coder la première ligne en binaire impose la seconde...etc.
On trouve vite que les 16 sont possibles avec un nombre pair de coups de 4 à 12.
solution n° 1 en 10 coups :
0 0 0 0
1 1 1 1
1 0 0 1
1 1 1 1
solution n° 2 en 6 coups :
0 0 0 1
1 1 0 0
1 1 0 0
0 0 0 1
solution n° 3 en 4 coups :
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
solution n° 4 en 8 coups :
0 0 1 1
1 0 1 1
0 1 0 0
1 0 1 0
solution n° 5 en 4 coups :
0 1 0 0
0 0 0 1
1 0 0 0
0 0 1 0
solution n° 6 en 8 coups :
0 1 0 1
0 0 1 0
1 1 0 1
1 1 0 0
solution n° 7 en 6 coups :
0 1 1 0
0 1 1 0
0 0 0 0
1 0 0 1
solution n° 8 en 10 coups :
0 1 1 1
0 1 0 1
0 1 0 1
0 1 1 1
solution n° 9 en 6 coups :
1 0 0 0
0 0 1 1
0 0 1 1
1 0 0 0
solution n° 10 en 6 coups :
1 0 0 1
0 0 0 0
0 1 1 0
0 1 1 0
solution n° 11 en 8 coups :
1 0 1 0
0 1 0 0
1 0 1 1
0 0 1 1
solution n° 12 en 12 coups :
1 0 1 1
0 1 1 1
1 1 1 0
1 1 0 1
solution n° 13 en 8 coups :
1 1 0 0
1 1 0 1
0 0 1 0
0 1 0 1
solution n° 14 en 12 coups :
1 1 0 1
1 1 1 0
0 1 1 1
1 0 1 1
solution n° 15 en 10 coups :
1 1 1 0
1 0 1 0
1 0 1 0
1 1 1 0
solution n° 16 en 10 coups :
1 1 1 1
1 0 0 1
1 1 1 1
0 0 0 0
#7 - 20-04-2018 22:20:31
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
EEchecs 23
Oups, j'ai répondu à "combien de coup pour finir le travail" 
Bref, avec les 3 premiers, ça fait 6.
La règle est que chaque case doit avoir un nombre de retournement impair.
Je réfléchi pour la suite.
#8 - 20-04-2018 22:30:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
ecjecs 23
@Gwen , j'ai plein d'autres solutions et je suis quasiment sûr que nous ne sommes pas sur le même problème 
Vasimolo
#9 - 20-04-2018 22:41:57
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,177E+3
zchecs 23
Postes-en une pour voir... 
#10 - 20-04-2018 22:48:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
echexs 23
Rien n'empêche de choisir plusieurs fois la même case .
Vasimolo
#11 - 20-04-2018 23:40:23
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,177E+3
exhecs 23
Arrête un peu ! Choisir une case une ou trois fois , aucune fois ou 2 fois, est idem. J'attends de te voir proposer une solution impaire pour dire que je n'ai pas compris le problème.
Sinon, je te fais tous les pairs de 4 à ..... une solution impaire est impossible sinon, elle ferait partie des 16 .
Modulo 2 pour chaque case, c'est imparable, on raisonne en base 2 pour la première ligne. Dire que tu en as beaucoup plus, c'est dire je sais faire "+2"
Dire que tu en as plus, c'est dire que tu as une solution impaire ? Je ne pense pas.
Après, prouver que la solution doit être paire et dire pourquoi, c'est autre chose. mais mes 16 tests suffisent en l'occurrence.
#12 - 21-04-2018 07:53:23
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
echrcs 23
Il faut montrer que tu as toutes les solutions , c'est là que réside la difficulté ( très relative ) .
Vasimolo
#13 - 21-04-2018 08:26:27
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,177E+3
echrcs 23
Je viens de le faire...
Si on a une solution valide, toutes celles modulo 2 sur chaque case le sont.
S'il n'y en a que 16 avec des 0 et des 1 et qu'elles sont toutes de total pair, aucune solution de total impair n'est possible.
#14 - 21-04-2018 08:42:35
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
rchecs 23
D'accord , ça épuise toutes les possibilités 
On peut aussi le montrer directement sans lister tous les cas avec une petite astuce .
Vasimolo
#15 - 21-04-2018 12:40:24
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Echecs 223
Salut Vasimolo,
le nombre de coups minimum est 4 : on retourne les pions de coordonnées (1;2), (2;4), (3;1) et (4;3). On ne peut pas faire mieux, car il y a 16 cases, et un coup retourne au plus 5 pions.
Les nombres de coups autorisés sont les nombres pairs >=4 : il est évident que ces nombres sont possibles, en jouant la même chose que ci-dessus, plus éventuellement un nombre pair de fois le même coup.
De plus, un nombre impair de coups ne serait pas possible : si on considère à nouveau les 4 pions de coordonnées (1;2), (2;4), (3;1) et (4;3), chacun des 16 coups possibles retourne exactement un de ces pions. Le nombre de pions noirs parmi ces 4 pions est donc pair après un nombre de coups pairs, et impair après un nombre de coups impairs.
#16 - 21-04-2018 17:36:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
ecgecs 23
Bien vu Ebichu 
Vasimolo
#17 - 22-04-2018 08:25:22
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3834
zchecs 23
A défaut de trouver l'astuce.....
On peut résoudre ce problème par de l'arithmétique modulo 2.
On numérote les cases de haut en bas et de gauche à droite (C1 à C4 en 1ère ligne en haut)
Chaque case a une valeur 0 ou 1, somme modulo 2 des variables échangées avec les voisines. Par exemple C1 = V1+V2+V5.
En posant que toutes les cases sont égales modulo 2 :
C1 = V1 + V2 + V5
C5 = V1 + V5 + V6 + V9
donne V2 = V6 + V9 (1)
C2 = C3 donne V1 + V6 = V4 + V7
C5 = C6 donne V1 + V9 = V2 + V7
qui donne V6+ V9 = V2 + V4. (2)
(1) et (2) implique V4 = 0
Par rotation, il en est de même pour V1, V13 et V16, c'est à dire les 4 cases d'angles.
Immédiatement, en reprenant C2 = C3, on a V6 = V7, et par rotation, V6 = V7 = V10 = V11.
En remplaçant les variables V7, 10, 11 par V6, et en supprimant les variables V1,4,13 et 16, on simplifie le systéme et on déduit :
V3 = V5, V2 = V8, V3 = V12, V8 = V15, V12 = V14, V5 = V14, V2 = V9.
égalités qui forment 2 quatuors de variables égales: {V3, V5, V12, V14} et { V2, V8, V9, V15}
En remplaçant V5, 12 et 14 par V2 et V8, 9, 15 par V2, le système n'a plus que 3 variables V2, V3, V6. Avec des cases V2+V3 et des cases V2+V3+V6.
On en déduit V6 = 0 et donc les 4 cases centrales.
Donc pour avoir l'égalité à 1 pour toutes les cases, seules peuvent être activées à 1 les cases du groupe {V3, V5, V12, V14} ou (exclusif) { V2, V8, V9, V15}.
#18 - 22-04-2018 09:05:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
rchecs 23
C'est marrant , tu as tous les éléments pour répondre en une phrase et tu passes à côté 
Regarde ce qui se passe avec les éléments de l'un des deux groupes que tu as obtenu si tu choisis une des 16 cases du jeu et que tu procèdes aux manœuvres de retournements .
Vasimolo
#19 - 23-04-2018 19:06:12
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
echzcs 23
En fait la solution tourne autour de cette figure mise en valeur par beaucoup :
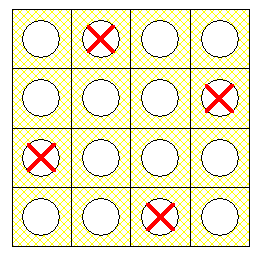
Si on choisit les cases marquées d'une croix on solutionne le problème en 4 coups . Ensuite chaque coup retourne exactement un pion d'une des cases cochées et on ne peut retourner le jeu qu'avec un nombre pair de coups strictement supérieur à 2 .
Merci aux participants 
Vasimolo
#20 - 25-04-2018 17:38:21
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3834
Echecs 223
Je m'étais planté dans mes équations....
Ce qui est curieux, c'est que le système d'équations ne permet pas d'exhiber les solutions, mais seulement de donner des relations entre les variables ( entre 2 ou plus ).
#21 - 25-04-2018 17:52:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Echces 23
Il y a beaucoup de paramètres dans le système et vouloir épuiser tous les cas ou réduire le système à une succession de coup n'est assurément pas la meilleure solution . Après c'est facile à dire quand on a vu la position clé ( mais tu l'avais trouvé ) . Activer les quatre croix retourne l'ensemble du jeu et n'importe quel coup retourne un unique pion marqué d'une croix : on a la clef du problème 
Vasimolo
#22 - 26-04-2018 08:35:02
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3834
echzcs 23
Euh...oui, la réponse je l'avaise comprise. En dehors de la recherche de l'énigme telle qu'elle a été posée, je pensais que le système d'équations pouvait permettre de résoudre ce problème, étant donné la simplification de calcul modulo 2. Il n'en est rien. En revanche, pour un carré 3*3, le système d'équations permet d'aboutir facilement à l'unique solution possible.
#23 - 26-04-2018 18:21:34
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
echexs 23
Je ne sais pas si c'est l'unique solution mais on retourne tous les pions en choisissant les quatre cases d'angles et la case centrale .
Vasimolo
PS : on avait vu dans un vieux problème que si on pose un nombre quelconque de pions faces blanches visibles sur les cases que l'on veut d'un échiquier , alors on peut toujours faire apparaître la face noire de l'ensemble des pions en retournant certains pions avec l'ensemble de ses voisins .
#24 - 01-05-2018 18:40:38
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
echecq 23
Bonjour,
J'ai fait quelques tests en python. En partant de 4x4 pions blancs, et en essayant les 2^16 façons de les retourner, on obtient 2^12 positions d'arrivée différentes, chacune obtenue de 16 façons différentes.
C'est pour ça que nodgim n'a pas pu résoudre le système.
En revanche, pour un système 2x2 ou 3x3, chaque postion d'arrivée s'obtient de façon unique, et toutes les positions d'arrivée sont atteignables.
J'ai voulu tester la matrice 5x5, mais le temps de calcul est rédhibitoire avec mon programme non optimisé.
#25 - 01-05-2018 19:11:45
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3834
Echec s23
Oui c'est ça Enigmatus.
La résolution du systèmes d'équations donne des solutions pour des couples de variables, des triplets, des quadruplets, ....
D'un point de vue pratique, ça n'aide pas beaucoup pour la recherche de tous les cas possibles. Enfin, perso, je n'ai pu m'en servir, mais il existe peut être une méthode qui permet de s'en sortir. Je n'ai pas assez approfondi le sujet.
La connaissance des relations obligées entre les variables nous aide t 'elle à trouver les solutions ? Ces relations nous disent ce qu'on ne peut pas faire, ce sont seulement des filtres.
Pour la grille 4*4, Gwen en a trouvé 16, mais par le jeu des symétries, ça fait nettement moins.
|
 |

 Accueil
Accueil
 Forum
Forum








