Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 19-08-2010 12:06:43
EEchecs 4Après les Dames , les pions
#0 Pub#2 - 19-08-2010 14:35:12#3 - 20-08-2010 10:52:44#4 - 20-08-2010 23:13:04#5 - 21-08-2010 11:03:22
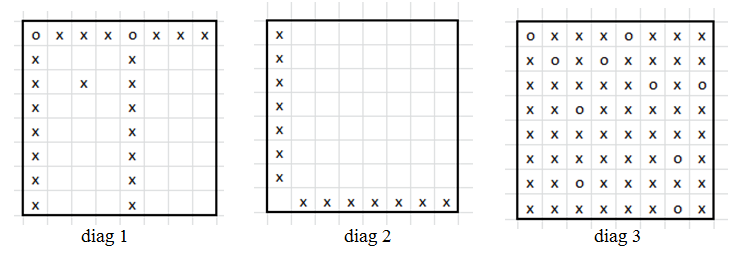
Echces 4Pourquoi ne peut-on pas faire mieux ? #6 - 21-08-2010 11:31:55
Ecchecs 4Je note tout d’abord que deux points sont sur une même ligne, les colonnes ne peuvent être utilisées car un triangle rectangle serait créé. The proof of the pudding is in the eating. #7 - 21-08-2010 12:07:35
echecq 4Deux démonstrations de dylasse pour le cas général et franck pour l'échiquier classique 8X8 . #8 - 23-08-2010 10:19:57
ecgecs 4Quand tu dit "les centres de trois quelconques d'entre eux ne forment jamais un triangle rectangle", tu entends quoi par centre ? le milieu du segment formé par deux pions ? ou bien chaque pion est un sommet du triangle ? #9 - 23-08-2010 17:25:33
echecd 4Tout le monde a trouvé la bonne réponse souvent par épuisement des cas . Je vous laisse quand même regarder la démonstration de dylasse pour le cas général . Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.