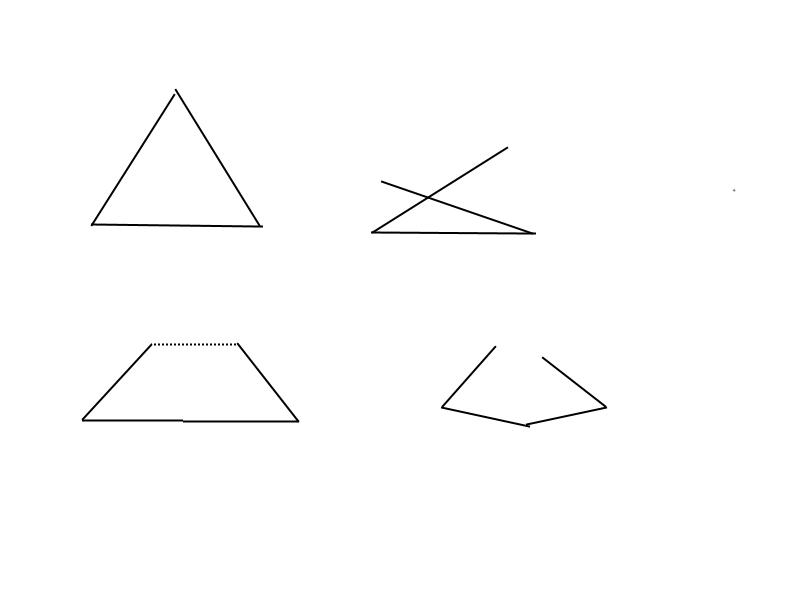|
#1 - 19-10-2016 18:27:42
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 20-10-2016 07:53:03
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
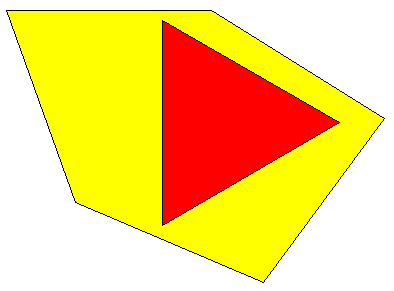
Gteau 128
Oui.
Du trapèze au triangle isocèle qu'on peut former avec le pentagone, on arrive toujours à inscrire le triangle équilatéral.
#3 - 20-10-2016 09:29:06
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
gâteay 128
Le pire des pentagones convexes serait un triangle isocèle de côtés 18; 18 et 9 cm (pentagone dégénéré) duquel on pourrait toujours extraire un triangle équilatéral de côtés 9 cm.
#4 - 20-10-2016 10:23:17
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteai 128
@Nodgim et Franky :
Si on fixe un côté du morceau de pâte , il y a deux degrés de liberté pour la construction du reste . S'il existe un contre-exemple , rien ne garantit qu'il y en aura un autre avec pour axe de symétrie la médiatrice du côté fixé ( ou alors il faut le justifier  ) . Clairement s'il y a un contre-exemple , il aura une drôle d'allure . ) . Clairement s'il y a un contre-exemple , il aura une drôle d'allure .
Bonne recherche 
Vasimolo
#5 - 20-10-2016 11:01:30
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
âGteau 128
D'instinct, je dirais que ça passe. Le cas aux limites d'aplatissement du pentagone est un triangle isocèle 9,18,18 et ça convient toujours, reste plus qu'à formaliser ça 
#6 - 20-10-2016 11:16:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtaeu 128
Tu as bien résumé le problème Scarta , après il faut mettre un peu les mains dans le cambouis ( rien de trop salissant tout de même  ) . ) .
Vasimolo
#7 - 20-10-2016 11:52:04
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Gâtaeu 128
Considérons un côté. Si l'angle à une de ses extrémités est inférieur à 60, l'autre est forcément supérieur, sinon croisement.
Et avec un nombre impair d'angles, on arrive forcément à la conclusion qu'un côté au moins du pentagone fait 2 angles de plus de 60 degrés.
Considérons ce côté, BC, avec les sommets A et D de part et d'autre.
Si les deux angles sont inférieurs à 120 degrés le triangle peut être construit dans ABCD et donc dans le pentagone. Inversement, si les deux sont supérieurs à 120, la figure n'est pas constructible (le pentagone lui-même)
Et si l'un des deux seulement est supérieur à 120, des relations trigonométriques nous donneraient BD, et donc les angles restants en A et D pour le quadrilatère ABCD. Ça marcherait et accessoirement le triangle serait même confiné à ABCD dans tous les cas, mais je suis sûr qu'on doit pouvoir faire plus simple...
#8 - 20-10-2016 12:35:01
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteeau 128
C'est un peu compliqué Scarta 
Tu affirmes que si un côté du pentagone fournit deux angles supérieurs à 60° alors on peut découper le gâteau en le posant sur ce côté ?
Vasimolo
#9 - 20-10-2016 13:45:37
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Gâtea u128
Entre 60 et 120, oui, obligatoirement.
Si l'un des deux est > 120, c'est moins trivial d'après ma méthode.
#10 - 20-10-2016 16:35:04
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteau 1128
On peut passer tous les cas de figure de cette façon :
On numérote le coté 1 la base, du coté 2 à 5 dans le sens horaire.
Le triangle restera, pendant tous les essais, base 1.
On part toujours d'une configuration symétrique base 1, longueur 1.
1er essai:
angle 23 = Pi. On fait diminuer angle 45, sans changer angle 23, jusqu'à symétrie coté 5. On finit sur un trapèze, juste avec un angle 12 pile 60°.
2ème essai:
angle 23 = Pi - epsilon. On fait diminuer angle 45, sans changer angle 23, jusqu'à symétrie coté 5. On se rend compte que le 2ème essai laisse plus de liberté au triangle placé base 1.
3ème essai
angle 23 encore un peu plus petit, et on recommence.
Les essais suivants sont pour la forme. Au derneir essai, on part du pentagone régulier, il n'y a plus de manoeuvre d'angle à faire.
Seul le 1er essai est critique, avec le trapèze au final. Mais ça passe.
Normalement, toutes les configurations ont été passées en revue. Le triangle est tjs resté à l'intérieur du pentagone.
#11 - 20-10-2016 22:41:54
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 1288
@Scarta : en effet ça marche dans le cas d'un angle inférieur à 120° et d'un supérieur mais c'est un peu lourd avec la trigo : on doit pouvoir s'en passer 
@Nodgim : pourquoi n'existe-t-il pas de contre-exemple sans axe de symétrie ?
Vasimolo
#12 - 21-10-2016 08:40:26
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteaau 128
L'expérience que j'ai réalisée ne se limite pas, bien évidemment, aux configurations symétriques. Je pars d'une situation symétrique depuis un coté (symétrie de la médiatrice de ce coté) jusqu'à une situation symétrique d'un coté adjacent, le passage de l'une à l'autre se faisant en continu (utilisation d'un mètre pliant). Cette méthode limite au strict minimum le nombre d'expériences à faire, elle exclut la redondance des situations symétriques.
Cela dit, même si c'est efficace et rend évident que ça marche toujours, c'est plus de la physique que des maths.
#13 - 21-10-2016 08:56:46
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
#14 - 24-10-2016 23:13:52
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
GGâteau 128
J'ai compris la "démonstration" de Nodgim (ce n''est pas vraiment des maths  ) , je n'ai pas vraiment compris les explications de Gwen ( c'est sûrement de ma faute ) . J'avais une solution avec plusieurs cas et calculs d'angles . ) , je n'ai pas vraiment compris les explications de Gwen ( c'est sûrement de ma faute ) . J'avais une solution avec plusieurs cas et calculs d'angles .
Merci aux participants 
Vasimolo
#15 - 25-10-2016 18:16:31
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
gâteay 128
J'ai compris la démonstration de Gwen, j'en était arrivé presque jusqu'au bout en suivant la même démarche, mais je n'avait pas poster car je n'avait pas le temps de la finir ce week end, et sur la fin, je n'avais pas remarqué ce très beau résultat de la droite qui touche sans cesse le triangle, je cherchait plutôt à éviter les calculs en placant les triangles contre l'un des deux autres côtés adjacents.
J'essaye de le réexpliquer:
Il est très facile de remarquer que l'on peut trouver deux côtés successifs supérieurs à 60 car il n'y en a pas plus d'un seul dans le pentagone: S'il y en a deux successifs, a 60 degrés, les trois côtés se referment en un triangle équilatéral, en deça, ça se croise, donc pas de pentagone. Sinon, si il y deux angles, alors il sont séparés par un seul angle.
Au cas limite, l'angle entre les deux est plat, et on obtient pile la place de refermer le pentagone si les deux angles sont à 60.
On a donc deux côtés successifs avec un angle de plus de 60.
Si l'on colle un coté du triangle entre ces deux angles, il ne sera pas coupé par les deux côtés adjacents (car ils s'écartent avec un angle trop grand).
La seule possibilité est qu'il soit coupé par l'un des deux côtés opposés.
Pour vérifier ce cas, on prend le pentagone le plus "plat" possible, c'est a dire en prenant l'angle opposé plat. Et ici, Gwen montre que ces deux côtés "frôlent le sommet de notre triangle sans le couper...
Quelques images a l'arrache:
En haut les cas ou les deux angles inférieurs à 60 sont côte à côte. En premier le cas limite ou ils sont égaux à 60, le deuxième ou ils sont iférieurs. Impossible d'obtenir le pentagone convexe.
Deuxième cas, ils sont séparés par un angle de plus de 60 degrés. En premier cas limite, en deuxième cas quelconque. La encore pas de pentagone...
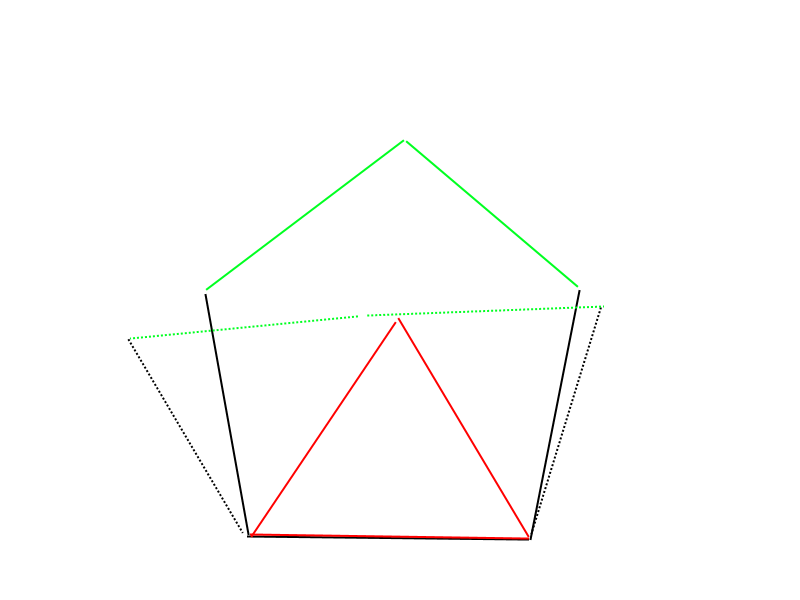
On place le triangle entre les deux angles de plus de 60 degrés. Pour avoir le cas limite, on aplatit l'angle (en pointillé) On obtient alors la droite qui frôle le triangle
#16 - 25-10-2016 23:16:50
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
âGteau 128
@Caduk
Es-tu vraiment sûr qu'on va pouvoir découper un triangle équilatéral sur un côté de la pâte à l'unique condition qu'il soit limité par deux angles supérieurs à 60° ?
Vasimolo
#17 - 25-10-2016 23:32:06
- caduk
- Professionnel de Prise2Tete
- Enigmes résolues : 45
- Messages : 398
âteau 128
Oui, c'est ce qui est expliqué par Gwen: il ne peut pas être coupé par les deux côtés latéraux, il ne peut donc être coupé que par les deux côtés supérieurs. On peut se limiter à considérer le cas ou l'angle supérieur est plat (sur la figure en pointillé) car c'est la position la plus "plate" possible. Dans cette configuration, Gwen a montré grâce à ces cercles que les deux côtés supérieurs ne coupent pas le triangle, mais passent par son sommet (voir son dernier message)
#18 - 25-10-2016 23:38:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gtâeau 128
Le dessin n'est pas très précis , mais il me semble bien que ça sort 
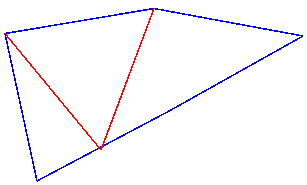
Vasimolo
#19 - 26-10-2016 08:24:03
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâtea u128
Réponse au dessin de Vasimolo
Pour la base il faut choisir le segment de gauche
#20 - 26-10-2016 08:53:54
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
Gâteau 18
Effectivement, ça touche.
Voir le dessin suivant avec un zoom sur la zone incriminée. Il faudrait une corde de rac(3) pour que ça marche...
Mais du coup ça m'a donné une autre preuve.
La corde du haut fait 2 de longueur. Le segment bleu fait 1. Le triangle dont 2 angles sont marqués est donc isocèle. Quand on décale la corde à gauche, la base de ce triangle augmente de longueur, si on la décale à droite , elle diminue de longueur.
Les angles marqué sont donc égaux et strictement croissant quand on décale la corde de gauche à droite.
Or, au milieu, on a vu que l'on obtenait un cas de figure avec des angles tous à 60°.
Dans le trapèze rouge, un des 2 angles supérieurs est donc toujours supérieur ou égal à 60°. Vu qu'il est convexe et de côtés plus grands que 1, on pourra toujours loger notre triangle soit le long du côté gauche, soit le long du côté droit.

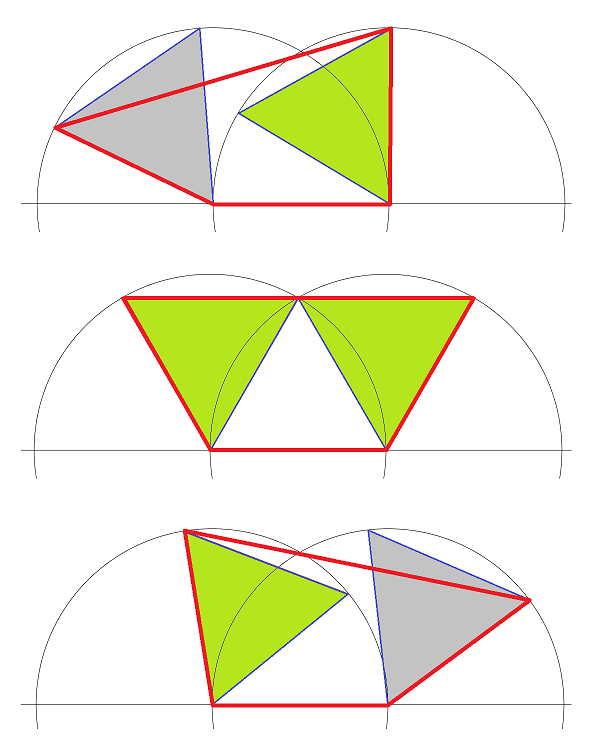
#21 - 26-10-2016 11:59:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteeau 128
Gwen , sur tes dessins il est clair qu'on case un triangle équilatéral de côté 1 dans un quadrilatère convexe de côtés : 1 , 1 , 1 , 2 . Ce que j'ai du mal à saisir , c'est comment tu ramènes le pentagone donné à ce quadrilatère qui serait pénible parmi les pénibles . Je ne mets pas de mauvaise volonté j'ai simplement du mal à voir comment le pentagone suit le mouvement lorsque tu fais basculer ton quadrilatère de gauche à droite .
Vasimolo
#22 - 26-10-2016 14:42:26
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
Gâteau 28
Je pars des 2 angles consécutifs à plus de 60° (en bas) en inscrivant le pentagone dans un des demi-plans.
Le cas traité est le cas limite où les 2 derniers ont un angle plat.
Après, on peut scinder le côté 2 en 1 et 1 en augmentant la convexité, mais ça ne change rien à la donne... on a juste une corde un peu plus petite que 2.
#23 - 26-10-2016 17:39:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtea 128
OK , Gwen , ça marche , sauf si la partie haute du quadrilatère est inférieure au côté du triangle .
Vasimolo
#24 - 26-10-2016 18:16:34
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,191E+3
Gtâeau 128
Non, ça marche tout le temps. 
Regarde sur la partie zoomée : elle est en dessous. Le triangle entre les 2 cercles n'intervient plus. Tant que la partie haute est plus grande que 1, il n'y a aucun souci.
Si elle est plus petite, on peut loger le triangle sur la base du quadrilatère, comme dans ma première idée car les 2 angles sont bornés à 60° (même à un peu plus de 75 en réalité..
#25 - 26-10-2016 18:25:30
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtteau 128
Quelque chose a dû m'échapper ( je n'ai pas toute ma tête en ce moment ) .
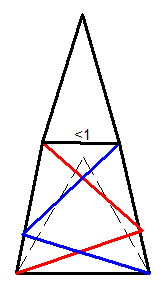
Vasimolo
PS : tu as répondu à ma question , pendant que je la posais 
|
 |

 Accueil
Accueil
 Forum
Forum