|
#1 - 12-12-2015 11:27:13
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtteau 113
Bonjour à tous .
Mon pâtissier a coupé un gâteau carré en 36 parts de la façon suivante :
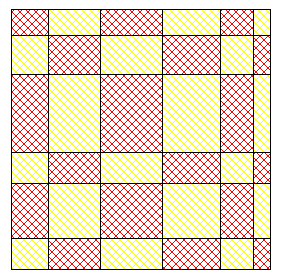
Il m’a donné toutes les parts carrées qui sont au nombre de cinq .
Suis-je certain d’avoir deux parts identiques ?
Amusez-vous bien 
Vasimolo
#2 - 12-12-2015 13:21:11
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Gâteau 11
Bonjour Vasimolo,
Suis-je certain d’avoir deux parts identiques ?
Je dirais oui.
On peut, pour faciliter le raisonnement, et sans nuire à la généralité du problème, trier les lignes et les colonnes par ordre de taille croissante.
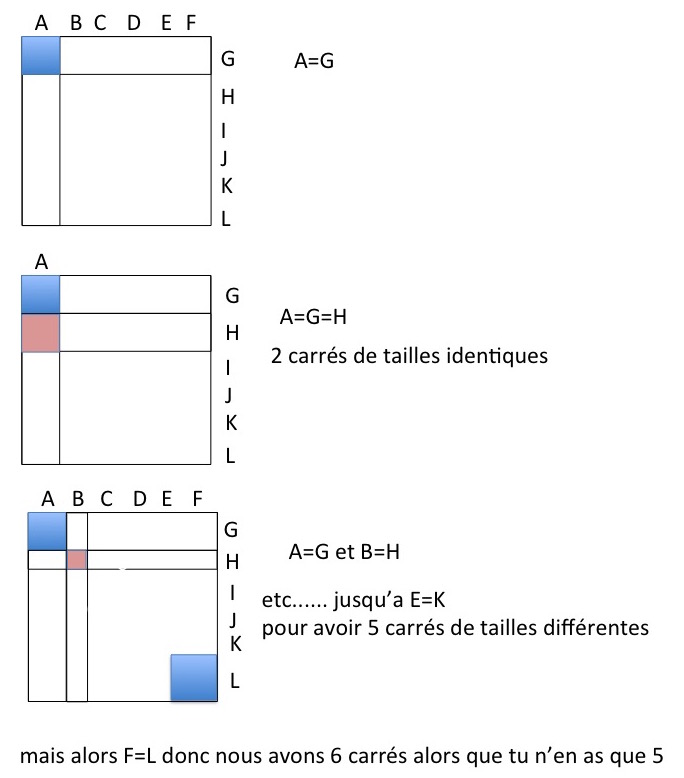
Si j'ai 5 parts différentes, elles sont obligatoirement situées sur la diagonale descendante, et il reste sur cette diagonale une case carrée qui est une 6ème part.
#3 - 12-12-2015 13:27:40
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gâteau 131
bonjour.
je ne vais pas faire de dessin . Mais par contre je peux dire que si 36 parts il y a ,
alors on peut couper 6 parts carrées avec chaque carré se situant sur des intersections de bandes différentes .Chaque ligne de rectangles comme chaque colonne de rectangles ne possède qu'un seul carré . il y a dans ce cas 6 carrés pas nécessairement différents. Par contre s'il n'y a que 5 carrés , deux sont automatiquement sur une bande horizontale ou une bande verticale.
#4 - 12-12-2015 14:42:18
- w9Lyl6n
- Professionnel de Prise2Tete
- Enigmes résolues : 26
- Messages : 239
GGâteau 113
Oui,
Si il y avait 5 carrés différents sur le gâteau, ils seraient sur 5 colonnes de largeur différentes, correspondant chacune à 5 lignes de hauteur égale. En soustrayant au coté du carré la somme de ces 5 largeurs puis la somme de ces 5 hauteurs identiques, on trouverait une ligne et une colonne supplémentaires de tailles identiques, qui se croiseraient en 6ème carré.
#5 - 12-12-2015 16:38:16
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteau 1113
Tentons d'éviter les doublons avec 5 carrés.
2 carrés ne peuvent se trouver sur la même ligne ou même colonne. Ce qui amène à dire que s'il y a comme largeurs a,b, c,d,e, il faut aussi comme hauteurs a,b,c,d,e (pas forcément dans cet ordre). Comme le gâteau est un carré, le reste de largeur ou de hauteur vaut C-a-b-c-d-e=f. ce qui donne obligatoirement un 6ème carré.
S'il y a exactement 5 carrés, il ne peuvent être tous sur des colonnes ou lignes distinctes, donc il y en a au moins 2 identiques.
#6 - 12-12-2015 17:26:20
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Gtâeau 113
Je dirais que oui.
- Soit deux bandes verticales (et deux bandes horizontales) ont la même largeur et dans ce cas, elles génèrent 4 parts carrées identiques.
- Soit 5 bandes verticales (et 5 bandes horizontales) sont de largeurs différentes, mais dans ce cas, les deux restes (verticalement et horizontalement) sont égaux et il y a forcément un sixième carré. Ce cas est donc à rejeter.
Tu auras donc toujours 4 parts carrées identiques.
#7 - 12-12-2015 17:41:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteu 113
@Enigmatus , Mathieu , Nodgim : oui 
@Unecoudée , Loozer : je n'ai pas compris 
Vasimolo
#8 - 12-12-2015 18:49:13
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Gâteau 13
Si 2 des 5 carrés sont "alignés", ils sont identiques (même largeur).
Si aucun n'est "aligné" avec un autre, il y a 5 bandes horizontales et verticales de même largeur 2 à 2 , au croisement de la dernière bande dans les deux sens, on aura un sixième carré ce qui est impossible à la lecture de l'énoncé.
Il a donc 2 parts identiques.
#9 - 12-12-2015 18:58:56
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gâeau 113
re
je veux dire ceci: s'il n'y a que 5 parts carrées , c'est qu'il y en a au moins 2 sur une même bande horizontale ou verticale . En effet , si ce n'est pas le cas , il y a
automatiquement une sixième part carrée à l'intersection de la sixième bande horizontale et de la sixième bande verticale. Puisque en sommant 5 côtés en horizontal et 5 mêmes côtés en vertical , le reste est de même longueur sur la sixième bande verticale et la sixième bande horizontale.
#10 - 12-12-2015 19:01:39
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâreau 113
@Gwen , Unecoudée : parfait .
Vasimolo
#11 - 12-12-2015 21:05:59
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Gâteu 113
Salut !
Alors rapidement, j'espère que ce sera clair :
On suppose qu'on a 5 carrés différents.
Comme ils sont différents, il ne sont ni sur la même ligne, ni sur la même colonne.
Par permutation circulaire, on peut déplacer les lignes (ou les colonnes) de manière à placer tous les carrés dans une diagonale du gâteau.
Du coup, le dernier quadrilatère qui se trouve dans la diagonale est aussi un carré (la diagonale du gâteau passe par 2 sommets de ce dernier quadrilatère).
Ainsi, si j'ai 5 carrés différents alors j'ai un sixième carré, ce qui dans l'énoncé est exclu.
Conclusion : Mon hypothèse de départ est fausse et j'ai donc au moins 2 carrés identiques (ce qui permet de les aligner et ainsi que casser cette démonstration).
#12 - 13-12-2015 11:37:46
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâyeau 113
C'est ça Golgot .
Vasimolo
#13 - 13-12-2015 13:12:18
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
Gâteau 13
Salut
Oui ( enfin je pense )
Je ne démontre rien. Ce n'est pas indiqué dans l'énoncé 
#14 - 13-12-2015 13:17:17
- dbab3000
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 111
Gtâeau 113
On considère:
A le côté du carré
xᵢ la largeur de la colonne i tel que 1≤i≤6 et x₁+x₂+x₃+x₄+x₅+x₆=A
yᵣ la largeur le de ligne r tel que 1≤r≤6 et y₁+y₂+y₃+y₄+y₅+y₆=A
Pour avoir une part de gâteau qui sera un carré il suffit que xᵢ=yᵣ
On a 5 carrés donc cette égalité est respecté 5 fois seulement.
Pour avoir deux carrés de même dimension il suffit que deux xᵢ ou deux yᵣ qui respectent l'égalité soient égaux.
Supposons par absurde qu'il n y pas de deux carrés égaux ce qui implique qu'aucun des xᵢ et yᵣ ne sont égaux.
Donnons un petit exemple
x₁=y₁, x₂=y₂,x₃=y₃,x₄=y₄ et x₅=y₅
Tous ces xᵢ ont des valeurs différentes
On peut dire que x₁+x₂+x₃+x₄+x₅+x₆= y₁+y₂+y₃+y₄+y₅+y₆
Ce qui implique que y₁+y₂+y₃+y₄+y₅+x₆= y₁+y₂+y₃+y₄+y₅+y₆
Ce qui implique que x₆=y₆
Alors on aura un 6 carré c'est absurde.
Donc on aura toujours deux carrés égaux si le nombre de carrés est 5.
Bonne journée.
#15 - 13-12-2015 17:44:00
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
gâyeau 113
Salut !
Si 2 des 5 carrés étaient sur la même ligne ou la même colonne, ils seraient de même côté, donc identiques.
Donc, si les 5 carrés sont différents, ils sont sur des lignes et colonnes différentes. Et la ligne et la colonne restantes ont la même épaisseur (C-c1-c2-c3-c4-c5). Elles forment donc un 6ème carré !
Conclusion : au moins 2 carrés ont la même taille.
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#16 - 13-12-2015 18:20:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 1133
@Dbab & Fix : oui 
@Nobodydy : tu as jeté un petit coup d’œil à la rubrique dans laquelle tu avais posté ton message , ici on n'est pas là pour rigoler : on démontre tout 
Vasimolo
#17 - 13-12-2015 22:17:35
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Gâteua 113
Je retente ma chance après avoir dit quelques bêtises.
Deux parts carrées appartenant à une même ligne ou une même colonne sont forcément identiques.
Si les parts carrées étaient toutes différentes, elles devraient donc appartenir à des lignes et colonnes différentes. Si x était le côté du gâteau et a, b, c, d, e étaient la longueur du côté des 5 carrés, il resterait donc une sixième colonne et une sixième ligne de largeur x-(a+b+c+d+e) et leur intersection donnerait une sixième part carrées.
Cette conclusion contredisant l'énoncé, il n'est donc pas possible d'avoir 5 parts carrées toutes différentes.
#18 - 13-12-2015 22:36:03
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Gâtea u113
Pour qu'il y ait des carrés, il faut que des intervales horizontaux soient égaux a des intervales verticaux. Je pense qu'il a alors 2 cas:
1) dans le premier cas: il y a au moins 2 intervales egaux, auquel cas, du fait qu'il y a deja 5 carrés, l'intersection du ou des intervales dans l'autre direction donne 2 carrés égaux.
2) dans l'autre cas tous les intervales sont differents, et donc pour qu'il y ait 5 carres, il faut au moins 5 intervales horizontaux = 5 intervales verticaux, et comme le gateau et carré, le sixieme intervale est aussi carré. Mais dans ce cas, il n'y a pas 2 carrés égaux.
oooops, j'avais mal lu...
en fait du fait qu'il y ait des carres, toute les autres parts sont identiques deux a deux, mais tournées a 90° l'une par rapport a l'autre.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#19 - 14-12-2015 05:30:36
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
gâtezu 113
Si deux carrés sont sur une même ligne ou colonne alors ils sont de même taille.
Pour que les cinq carrés ne soient pas de même taille il faut donc qu’ils soient sur des lignes et colonnes différentes mais alors la case de la ligne-colonne non occupée est encore un carré et il y en a 6.
#20 - 14-12-2015 11:42:04
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
Gâteu 113
Je pense que oui.
Si les 5 parts sont toutes de dimensions distinctes, il s'agit de a², b², c², d², e²,
la ligne et la colonne restantes auraient la même hauteur/largeur, ce qui ferait 6 carrés et non pas 5.
#21 - 14-12-2015 11:46:45
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
#22 - 14-12-2015 14:21:33
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtea u113
C'est bon pour tout le monde 
Vasimolo
#23 - 15-12-2015 00:05:49
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
gâtrau 113
Salut,
Raisonnement par l'absurde :
Si les 5 parts carrées sont différentes, de côté l1, l2, ... l5, alors deux d'entre elles ne peuvent pas être ni sur la même ligne, ni sur la même colonne (sinon elles auraient même côté, donc seraient identiques).
Les 5 parts sont donc sur des lignes et des colonnes différentes.
La part qui se trouve sur la 6ème ligne et la 6ème colonne est alors elle aussi carrée (car de longueur et de largeur égales à L - l1 - l2 - l3 - l4 - l5). Il y a donc 6 parts carrées, ce qui contredit l'hypothèse de 5 parts carrées.
CQFD.
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#24 - 15-12-2015 17:27:37
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteay 113
Bravo et merci à tous 
Vasimolo
#25 - 15-12-2015 19:37:37
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gtâeau 113
Merci à toi pour toutes tes énigmes.
|
 |

 Accueil
Accueil
 Forum
Forum