 |
#1 - 09-11-2019 15:39:36
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Les trois cercles nscrits
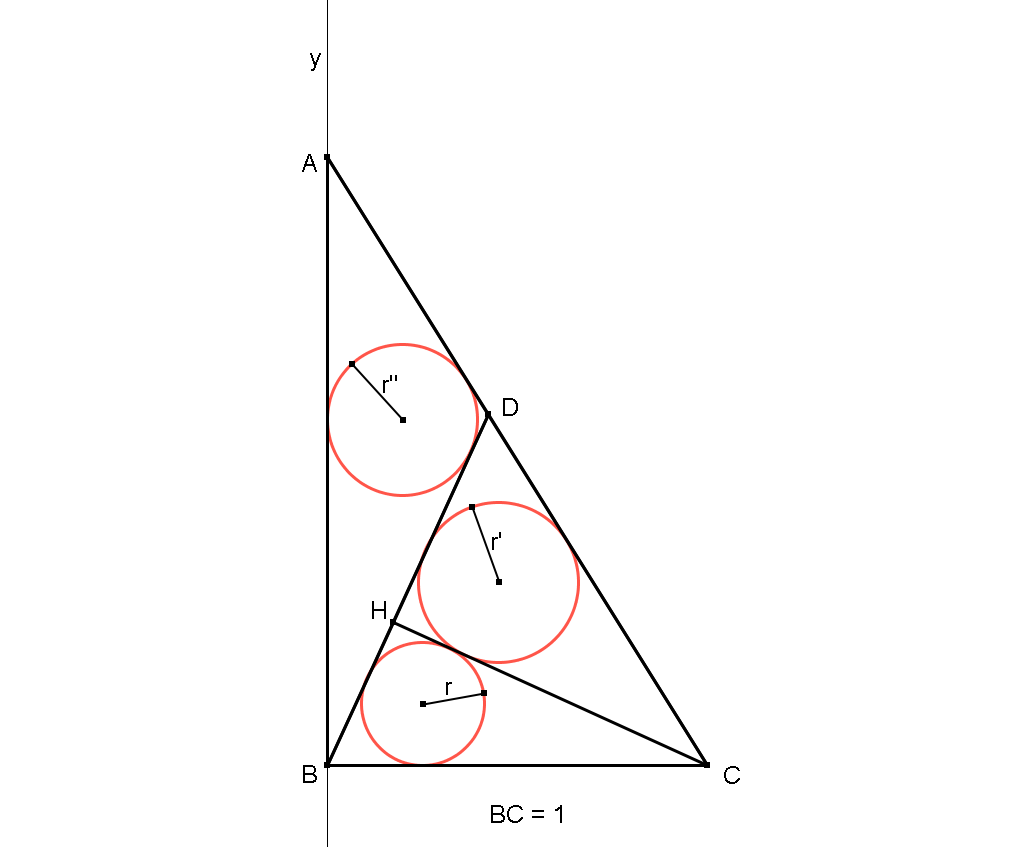
Bonjour .
Je propose un problème de géométrie pour changer du précédent .
Le voici :
On trace un segment invariable BC de longueur l'unité ;
Puis on trace la demi-droite By perpendiculaire à BC .
Soit A , un point variable sur la demi-droite By , les points A & B sont distincts .
On trace le segment AC . Le triangle ABC est donc rectangle en B
Soit D un point variable sur le segment AC; on trace le segment BD et enfin la hauteur CH issue de C dans le triangle BCD .
Nous obtenons alors 3 triangles : ABD , CHB & CHD .
On trace enfin les cercles inscrits dans ces 3 triangles .
La construction est terminée .
Le but de la manipulation est de déplacer les 2 points : A , sur la demi-droite By , et D sur le segment AC et faire en sorte que les 3 cercles inscrits soient égaux .
Dans ce cas que vaut leur rayon ? donner les 7 premières décimales . (pas de logiciel de CAO)
A justifier donc .
Bon courage .
#2 - 11-11-2019 11:42:05
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
les trois cercles insvrits
Salut,
on remarque déjà que pour que le tracé de [BH] donne deux cercles de même rayon, il faut que BCD soit isocèle en C, donc CD = 1.
On pose ensuite AC=a. Le rayon d'un cercle inscrit dans un triangle se calcule par 2A/p, où A et p sont respectivement l'aire et le périmètre du triangle. En numérotant 1 et 2 les triangles ABD et CHD, il vient :
[TeX]2A_1=\left(1-\frac{1}{a}\right)\sqrt{a^2-1}[/TeX]
[TeX]p_1=\sqrt{a^2-1}+a-1+\sqrt{2}\sqrt{1-\frac{1}{a}}[/TeX]
[TeX]2A_2=\frac{\sqrt{a^2-1}}{2a}[/TeX]
[TeX]p_2=1+\frac{\sqrt{2}}{2}\left(\sqrt{1-\frac{1}{a}}+\sqrt{1+\frac{1}{a}}\right)[/TeX]
En écrivant que r1=r2, puis en simplifiant l'équation obtenue (je passe les calculs assez lourdingues), il vient que a est la plus grande solution de l'équation :
[TeX]8a^3-8a^2-23a+25=0[/TeX]
Il ne reste plus qu'à reporter dans les formules plus haut, et on obtient que r vaut environ 0,1646000.
Était-ce la méthode attendue ?
#3 - 11-11-2019 17:34:03
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Les trois cerces inscrits
bonjour,
Et de une bonne réponse
@Ebichu : bravo à toi ! Il y aurait au moins 2 méthodes ; mais alors complètement différentes .
à plus .
#4 - 12-11-2019 03:22:51
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3236
- Lieu: Luxembourg
les trois cercles unscrits
A coups de triangles semblables (voire identiques), je
trouve: R = (V3 - 1) / 4 = env. 0,1830127
Je passerai plus tard pour détailler mon raisonnement.
Edit: Explications:
En abaissant D perpendiculairement sur BC au point I,
les triangles BDI et BCH sont identiques.
Donc le triangle BCH BCD est isocèle en B.
Un raisonnement similaire donne qu'il aussi isocèle en C.
Donc le triangle BCH BCD est équilatéral.
Pour le reste, un calcul élémentaire indique le rayon des
cercles inscrits (avec R = 2.S/P) identique pour les trois
cercles.
#5 - 12-11-2019 15:35:12
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
les troiq cercles inscrits
bonjour ,
@Franky : CH est la hauteur issue de C ; donc perpendiculaire à BD . BCH étant
rectangle en H ne peut pas être équilatéral .
@Ebichu : en y regardant de plus près , [latex]2A_1 = (1-\frac1a) . \sqrt{a^2-1}[/latex] non ?
#6 - 12-11-2019 18:41:05
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3236
- Lieu: Luxembourg
Les trois cercles inscritts
Je me suis planté dans le nom du triangle: c'est BCD qui est
équilatéral (et non BCH): j'ai corrigé dans mon post initial.
#7 - 12-11-2019 18:59:00
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Les trois ccercles inscrits
Tout à fait, erreur de copier-coller, désolé. Ça ne remet pas en cause la suite. J'ai corrigé le message.
#8 - 12-11-2019 20:03:59
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
les trois cercles insvrits
@Franky : les deux triangles BDI & BCH sont semblables , pas égaux .
#9 - 14-11-2019 12:21:21
- TOUFAU
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 105
Les trois cercles inscrtis
Bonjour,
Je trouve R=0,1646000 (modulo toute erreur de calcul possible, mais malvenue).
R=R’ impose que BHC et DHC soient égaux : ils sont tous deux rectangles en H, partagent leur base (HC), et le cercle inscrit est strictement croissant avec la hauteur.
J'appelle x la longueur BH (ou HD) et a la longueur (BA). Si Xd et Yd sont les coordonnées de D dans le repère BC, BA, on trouve
Xd = 2x²
Yd=2x*√(1-x²)
Puis a = Yd/(1-Xd)=2x√(1-x²)/(1-2x²)
Le rayon d’un cercle inscrit dans un triangle vaut 2S/P, S et P étant respectivement la surface et le périmètre (démo triviale sous wikipédia 😊)
Je trouve
R = x√(1-x²)/(1+x+√(1-x²))
R’’ = (a-2x√(1-x²))/(a+√(1+a²)+2x-1)
En remplaçant a par sa valeur en x, et après simplification, R=R’’ donne
10*x^3 + 2*x^2-5x+1=0 solution, avec x respectant les conditions 4x²+x-1>0 et x<1/√2
La seule solution vaut 0,4231320829, et donne R=0,1646000
J’ai tenté un schéma pour vérifier, malheureusement pas hyper probant…
#10 - 14-11-2019 16:45:47
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
les rrois cercles inscrits
Bonjour ,
@Toufau : bravo pour ta réponse ; par contre , peux-tu m'éclairer ?
c'est ok pour les coordonnées de D ; mais que représentent a & h dans ta démonstration ?
#11 - 14-11-2019 20:49:24
- TOUFAU
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 105
Lse trois cercles inscrits
Salut Unecoudée
a c'est ton a à toi (BA)
d et h c'est une 'double notation'
d=Xd et h=Yd. pour tromper l’ennemi, et rendre illisible des choses simples :-)
Bien vu...
PS: j'ai modifié dans le premier post
#12 - 16-11-2019 11:19:56
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Les troois cercles inscrits
Bonjour ,
et merci à tous les participants . Je suis parti avec les angles .
Voici donc ma proposition :
Excusez de l'absence du Latex , gros problème , la mise en page est affreuse .
Résolution :
Tout d'abord , il va de soi que les 2 cercles inscrits dans les 2 triangles rectangles sont égaux que lorsque ces derniers le sont .
CH est donc bissectrice de l'angle C .
On va d'abord rechercher tous les angles des deux triangles ABD & BCH . On pose : angle HBC = Ø
ABD a pour angles : pi/2 - Ø ; pi - Ø ; 2Ø - pi/2 .
BCH a pour angles : Ø ; pi/2 - Ø ; pi/2 .
On connaît donc aussi tous leurs angles moitiés . Et pour chacun des deux triangles , on prend respectivement pour base les côtés BD et BC dont on peut écrire les valeurs :
BC = 1 ; BD = 2cos Ø .
Dans un triangle scalène ABC , le rayon de son cercle inscrit est donné en fonction d'un des côtés :a = BC (par exemple) , des sinus des deux demi angles B/2 & C /2 adjacents et du cosinus du demi angle opposé A/2 .
R = a x sin (B/2) x sin (C/2) / cos (A/2 ) .
1) les cercles inscrits des 2 triangles BHC & ABD sont égaux , alors : BD = 2 Cos Ø . On peut donc écrire l'égalité suivante :
Sin (Ø/2) x Sin [pi/4 - Ø/2] / Cos (pi/4) = 2 Cos Ø x Sin [pi/2 - Ø/2] x Sin [pi/4 - Ø/2] / Cos [Ø - pi/4]
Sin (Ø/2) / Cos (pi/4) = 2 Cos Ø x Sin [pi/2 - Ø/2] / Cos [Ø - pi/4]
En utilisant les formules trigo : Cos (a + b) , Sin (a + b) .....
V2 x Sin (Ø/2) = 2V2 x Cos Ø x Cos (Ø/2) / [ Cos Ø + Sin Ø ]
Tan (Ø/2) = 2 Cos Ø / [ Cos Ø + Sin Ø ] (1)
On pose t = Tan (Ø/2) , donc Cos Ø = (1 - t²) / (1+t²) , puis Sin Ø = 2t / (1+t²)
On reporte tout ça dans l'équation (1) :
t = [ 2 x (1-t²)/(1+t²) ] / [ (1-t²+2t)/(1+t²) ]
t = ( 2 - 2t² ) / ( 1 - t² + 2t ) donne l'équation finale de degré 3
t³ - 4t² - t + 2 = 0 donne t = 0.63667176207.. qui est la tangente de l'arc Ø/2 = 32°.483756 .
Ø = 64°.9675124933...
Dans le triangle rectangle BHC , on peut calculer R :
R = ( Sin Ø + Cos Ø - 1 ) / 2 = 0.1646000 unité . CQFD
|
 |

 Accueil
Accueil
 Forum
Forum







