|
#1 - 13-09-2013 14:45:32
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
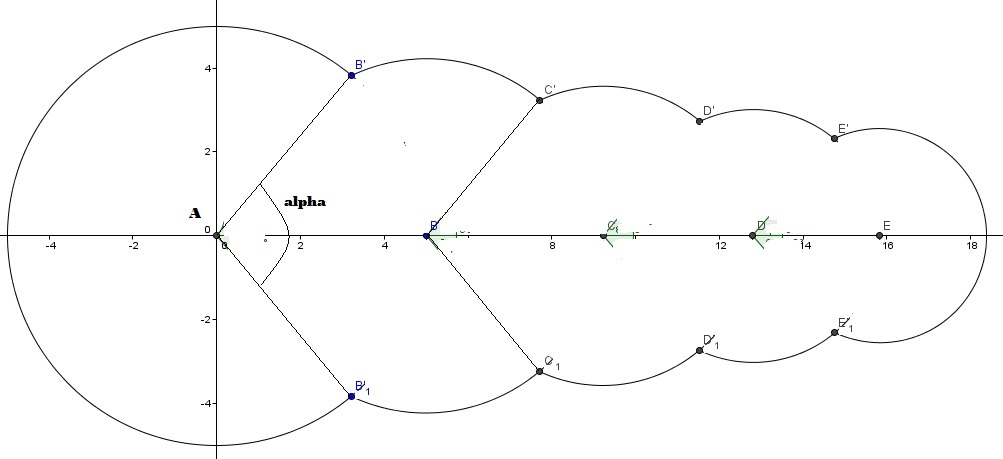
Le vieux dossier de Grand-Pèree : N°6 (une suite de cercles?)
#2 - 14-09-2013 08:54:01
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le viex dossier de Grand-Père : N°6 (une suite de cercles?)
#3 - 14-09-2013 11:14:58
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
le vieux dossier de grand-pèrz : n°6 (une suite de cercles?)
Bonjour, 
c'est vrai que celui-là est un peu plus costaud.
Ce n'est pas encore pour poster une solution, mais juste pour signaler que dans ton énoncé Cn désigne le n-ième cercle, mais aussi un point d'intersection entre Cn+1 et ... Cn  . .
Il y a sûrement plus simple.
#4 - 14-09-2013 11:28:01
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le vieux dossier de Grand-Père : N°6 (une suuite de cercles?)
cogito a écrit:
Ce n'est pas encore pour poster une solution, mais juste pour signaler que dans ton énoncé Cn désigne le n-ième cercle, mais aussi un point d'intersection entre Cn+1 et ... Cn.
Merci cogito pour la remarque, je viens de remédier à ca 
Cn est bien la n-ième cercle. Bn et Dn sont donc les intersections entre Cn et Cn+1.
#5 - 14-09-2013 12:22:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
le cieux dossier de grand-père : n°6 (une suite de cercles?)
Le problème n'est pas difficile , l'aire recherchée est 2(D+T1+Q1+T2+....+F) , le calcul est vraiment facile .

Après pour les autres questions , c'est vraiment scolaire mais y'en a qui aiment 
Vasimolo
#6 - 14-09-2013 13:31:31
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
le vieux dossier de grand-père : n°6 (une suite de vercles?)
Comme dit vasimilo, le calcul de l'aire de n'est pas difficile en soit si on divise bien la section à calculer mais le but du sujet de calculer l'aire en connaissant le nombre de cherche, le rayon initial R et [latex]\alpha[/latex]. Donc vasimolo, tu donnes une méthode mais pas la réponse  . .
#7 - 14-09-2013 19:20:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Le vieux dossier de Grad-Père : N°6 (une suite de cercles?)
#8 - 15-09-2013 00:12:00
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
L evieux dossier de Grand-Père : N°6 (une suite de cercles?)
Après avoir amélioré le dessin de kossi_tg  : :
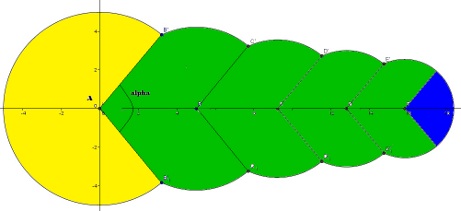
On a Sn qui est égal à l'aire du pacman jaune plus l'aire des pacman verts plus l'air du fantôme bleu (du moins ce qu'il en reste  ). L'air en vert se décompose en (n-1) parties identiques qui sont chacune déterminée pour chaque [latex]1\le k < n[/latex] par les points [latex] B_kA_kD_kD_{k+1}A_{k+1}B_{k+1}[/latex]. Appelons [latex]V_k[/latex] l'aire délimitée par ces points (je ne parle pas du polygône, [latex]D_kD_{k+1}[/latex] et [latex]B_{k+1}B_k[/latex] sont des arcs de cercle). ). L'air en vert se décompose en (n-1) parties identiques qui sont chacune déterminée pour chaque [latex]1\le k < n[/latex] par les points [latex] B_kA_kD_kD_{k+1}A_{k+1}B_{k+1}[/latex]. Appelons [latex]V_k[/latex] l'aire délimitée par ces points (je ne parle pas du polygône, [latex]D_kD_{k+1}[/latex] et [latex]B_{k+1}B_k[/latex] sont des arcs de cercle).
Alors on a :
[TeX]S_n={\color[rgb]{1,0.8,0} R_1^2{(2\pi-\alpha)\over 2}}+ {\color[rgb]{0,0.6,0} \sum_{k=1}^{n-1} V_k} + {\color{blue} R_n^2{\alpha\over 2}}={\color[rgb]{1,0.8,0} R_1^2(\pi-{\alpha\over 2})}+ {\color[rgb]{0,0.6,0} \sum_{k=1}^{n-1} V_k} + {\color{blue} R_n^2{\alpha\over 2}}[/TeX]
Dans tout ce qui suit, je ferais référence à la figure suivante :
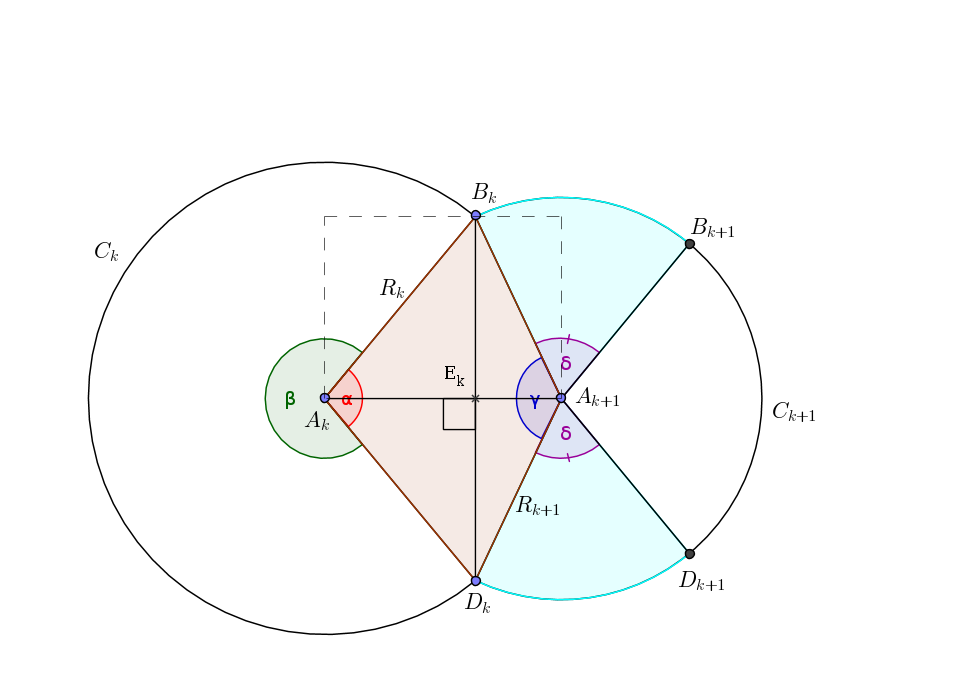
Nous voulons donc calculer l'aire des [latex]V_k[/latex], ce qui correspond à l'air en rouge plus l'air en bleu ciel sur la figure.
Calcul de l'aire en rouge :
L'aire du polygone en rouge est égale à l'air du rectangle en pointillé et vaut donc [latex]B_kE_k*A_kA_{k+1}[/latex]. (bon d'accord, pour alpha plus grand que pi/2 c'est plus dur à voir, mais c'est toujours vrai, j'ai donné cet argument pour ne pas avoir à détailler les calculs  ) )
Nous avons d'une part [latex]A_kA_{k+1}=R_k[/latex] et d'autre part [latex]B_kE_k=R_k\sin{\alpha\over 2}[/latex]
Donc finalement, l'aire en rouge est égale à [latex]R_k^2\sin{\alpha\over 2}[/latex].
Calcul de l'aire en bleu ciel :
L'aire en bleu ciel est égale à [latex]2(R_{k+1}^2{\delta\over 2})[/latex].
D'une part, comme l'angle [latex]\widehat{B_kA_kD_k}[/latex] est un angle au centre, et que [latex]\widehat{B_kA_{k+1}D_k}[/latex] est un angle inscrit qui intercepte le même arc alors nous avons :
[TeX]\gamma={\beta\over 2}[/TeX]
D'autre part nous avons [latex]\gamma + 2\delta = \beta[/latex] et donc nous avons
[TeX]2\delta={\beta\over 2}={(2\pi-\alpha)\over 2} = \pi-{\alpha\over 2}[/TeX]
Donc finalement l'aire en bleu ciel est égale à [latex]R_{k+1}^2({\pi\over 2}-{\alpha\over 4})[/latex].
Pour résumé cela nous donne :
[TeX]{\color[rgb]{0,0.6,0} V_k} = {\color[rgb]{0.7,0,0}R_k^2\sin{\alpha\over 2}} + {\color[rgb]{0.2,0.7,0.7}R_{k+1}^2({\pi\over 2}-{\alpha\over 4})}[/latex].
Maintenant, il ne reste plus qu'a trouver la relation entre les rayons des cercles.
Si on regarde le triangle [latex](A_kA_{k+1}D_k)[/latex], c'est un triangle isocèle dont la base est de longueur [latex]R_{k+1}[/latex] et dont les deux autres côtés sont de longueurs [latex]R_k[/latex] et dont l'angle au sommet vaut [latex]\alpha/2[/latex]. On a donc [latex]R_{k+1}=2R_k\sin{\alpha\over 4}[/latex].
Cette relation nous permet d'une part, par une récurrence directe, d'exprimer [latex]R_k[/latex] pour tout k :
[latex]R_k=(2sin{\alpha\over 4})^{k-1}R_1[/TeX]
d'autre part de trouver un terme général pour [latex]V_k[/latex], en effet :
posons [latex]x=\sin{\alpha\over 2}[/latex], [latex]y=\sin{\alpha\over 4}[/latex] et [latex]z={\pi\over 2}-{\alpha\over 4}[/latex], alors nous avons :
[TeX]V_{k+1}= R_{k+1}^2x+R_{k+2}^2z = (2R_ky)^2x+ (2R_{k+1}y)^2z=(2y)^2(R_k^2x+R_{k+1}^2z)=4y^2V_k[/TeX]
et donc par une récurrence directe nous avons pour tout k:
[TeX]V_k=(4y^2)^{k-1}V_1=(4(\sin{\alpha\over 4})^2)^{k-1}V_1[/TeX]
avec [latex]V_1 = R_1^2\sin{\alpha\over 2} + R_2^2({\pi\over 2}-{\alpha\over 4})}[/latex].
et donc finalement, pour en revenir à nos pacman  : :
[TeX]S_n= {\color[rgb]{1,0.8,0} R_1^2(\pi-{\alpha\over 2})}+ {\color[rgb]{0,0.6,0} \sum_{k=1}^{n-1} (4y^2)^{k-1}V_1} + {\color{blue} R_n^2{\alpha\over 2}}[/TeX][TeX]{\color{white} S_n}= {\color[rgb]{1,0.8,0} R_1^2(\pi-{\alpha\over 2})}+ {\color[rgb]{0,0.6,0} V_1\sum_{k=1}^{n-1} (4y^2)^{k-1}} + {\color{blue} ((2sin{\alpha\over 4})^{n-1}R_1)^2{\alpha\over 2}}[/TeX][TeX]{\color{white} S_n}= {\color[rgb]{1,0.8,0} R_1^2(\pi-{\alpha\over 2})}+ {\color[rgb]{0,0.6,0} V_1\sum_{k=0}^{n-2} (4y^2)^k} + {\color{blue} R_1^2(4y^2)^{n-1}{\alpha\over 2}}[/TeX]
cas 1 : [latex]\mathbf{4y^2 = 1}[/latex] alors on a :
[TeX]S_n= {\color[rgb]{1,0.8,0} R_1^2(\pi-{\alpha\over 2})}+ {\color[rgb]{0,0.6,0} V_1\sum_{k=0}^{n-2} 1} + {\color{blue} R_1^2{\alpha\over 2}} =R_1^2\pi +(n-1)V_1[/TeX]
Dans ce cas là, Sn diverge et nous avons :
[TeX]4y^2= 1\Leftrightarrow y^2={1\over 4}\Leftrightarrow sin{\alpha\over 4}= \pm {1\over 2}[/latex].
Comme on choisit [latex]\alpha\in[0,2\pi][/latex] alors [latex]{\alpha\over 4}\in[0,{\pi\over 2}][/latex], et la seul solution de l'équation ci-dessus qui soit dans cet intervalle est [latex]{\alpha\over 4}={\pi\over 6} \Leftrightarrow \alpha={2\pi\over 3}[/TeX]
Interprétation géométrique de ce résultat :
Si on trace les deux droites qui sont tangentes à tous les cercles, alors ces deux droites sont parallèles. Tous les cercles ont le même rayon. Et donc Sn diverge.
cas 2 : [latex]\mathbf{4y^2 \neq 1}[/latex]
Nous pouvons alors utiliser la formule des série géométriques pour calculer la somme en vert :
[TeX]S_n= {\color[rgb]{1,0.8,0} R_1^2(\pi-{\alpha\over 2})}+ {\color[rgb]{0,0.6,0} V_1{1-(4y^2)^{n-1}\over 1-4y^2}} + {\color{blue} R_1^2(4y^2)^{n-1}{\alpha\over 2}}[/TeX]
Nous voyons donc que [latex]S_n[/latex] converge si et seulement si la suite définie par [latex]u_n=(4y^2)^n[/latex] converge. [latex]u_n[/latex] converge si et seulement si :
[TeX]|4y^2|< 1\Leftrightarrow x^2 < {1\over 4}\Leftrightarrow |sin{\alpha\over 4}|< {1\over 2}[/TeX]
De la même manière que dans le cas précédent on obtient que [latex]\alpha < {2\pi\over 3}[/latex]. Donc la suite [latex]S_n[/latex] converge si [latex]\alpha < {2\pi\over 3}[/latex] et diverge sinon.
Interprétation géométrique de ce résultat :
Si [latex]\alpha<{2\pi\over 3}[/latex] alors les deux droites qui sont tangentes à tous les cercles se coupent dans la partie droite du dessin et forment ainsi un triangle dont l'aire majore Sn, donc Sn converge.
Sinon les droites se rejoignent de l'autre côté du dessin, cela signifie que l'on aura des cercles de plus en plus grand, et donc que Sn diverge.
Donc dans le cas où [latex]\alpha < {2\pi\over 3}[/latex] nous avons :
[TeX]4y^2 <1[/latex], et donc la suite [latex]u_n[/latex] converge vers 0, et donc [latex]S_n[/latex] converge vers :
[latex]{\color[rgb]{1,0.8,0} R_1^2(\pi-{\alpha\over 2})} + {\color[rgb]{0,0.6,0} {V_1\over 1-4y^2}}[/TeX]
Application numérique :
Pour [latex]R_1 = 5, n= 20[/latex] et [latex]\alpha={5\pi\over 9}[/latex] on a :
[TeX]y = \sin{5\pi\over 36}[/TeX][TeX]R_2 = 2yR_1 = 10\sin{5\pi\over 36}\simeq 4,22618[/TeX][TeX]V_1 = 5^2\sin{5\pi\over 18} + R_2^2({\pi\over 2}-{5\pi\over 36})}= 25\sin{5\pi\over 18} + R_2^2({13\pi\over 36})}\simeq 39,413341[/TeX][TeX]4y^2=4\sin^2{5\pi\over 36}\simeq 0,7144[/TeX][TeX](4y^2)^{19}\simeq 0,001679[/TeX][TeX]{1-(4y^2)^{19}\over 1-4y^2}\simeq 3,49582[/TeX]
[TeX]S_{20} \simeq {\color[rgb]{1,0.8,0} 25*{13\pi\over 18}} + {\color[rgb]{0,0.6,0}39,413341*3,49582} + {\color{blue} 25* 0,001679 * {5\pi\over 18}}\simeq 194,542[/TeX]
Ouf ! J'espère ce n'est pas trop confus.
Je me suis beaucoup amusé à faire se poste là  , j'espère que les couleurs sont lisibles , j'espère que les couleurs sont lisibles  . .
Pour la 3D je verrais ça plus tard peut-être.
Il y a sûrement plus simple.
#9 - 15-09-2013 00:16:55
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le vieux dossier de Grand-Père : N6 (une suite de cercles?)
#10 - 15-09-2013 15:54:00
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
le vieux dossier de grand-père : n°6 (une suite de cerckes?)
Bonjour,
Voici la réponse aux questions 1), 2) et 3).
Question 1
[TeX]S_n=\pi R^2+\left[4\sin^2{\frac{\alpha}{4}}\left(\pi+\frac{\alpha}{2}+\sin\frac{\alpha}{2}\right)-\alpha+\sin\alpha\right] \frac{\ 1-4^{n-1}\sin^{2n-2}\frac{\alpha}{4}\ }{\ 1-4\sin^2\frac{\alpha}{4}\ }\,\frac{R^2}{2}[/TeX]
Question 2
La suite [latex]S_n[/latex] converge si et seulement si [latex]4\sin^2\frac{\alpha}{4}<1[/latex], c-à-d [latex]\alpha<\frac{2\pi}{3}[/latex] (120°).
Dans ce cas la limite est
[TeX]S=\pi R^2+\left[4\sin^2{\frac{\alpha}{4}}\left(\pi+\frac{\alpha}{2}+\sin\frac{\alpha}{2}\right)-\alpha+\sin\alpha\right] \frac{ 1}{\ 1-4\sin^2\frac{\alpha}{4}\ }\,\frac{R^2}{2}[/TeX]
Notons que pour [latex]\alpha=\frac{2\pi}{3}[/latex] tous les cercles ont le même rayon.
3) [latex]S_{20} = 194.5419201720921144789774856...[/latex] arrondi à [latex]194.542[/latex]
[TeX]S = 194.7370706227094117208196155...[/TeX]
Voilà !
#11 - 16-09-2013 09:02:36
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le vieux dossier de Grand-Père : N°6 (une suite de ccercles?)
BRAVO masab 
#12 - 16-09-2013 15:20:30
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Le vieux doossier de Grand-Père : N°6 (une suite de cercles?)
Question 4
On pose [latex]g(x)=\sin^4\frac{x}{4}\left(2+\cos\frac{x}{2}\right)[/latex] .
Pour [latex]\alpha\not=\frac{2\pi}{3}[/latex] , on a
[TeX]V_n=\frac{4}{3}\pi R^3\left(8\sin^3\frac{\alpha}{4}\right)^{n-1}+\frac{4}{3}\pi R^3\left[ 1-g(\alpha)-8\sin^3\frac{\alpha}{4}\,g\left(\pi-\frac{\alpha}{2}\right)\right] \frac{\ 1-\left(8\sin^3\frac{\alpha}{4}\right)^{n-1}\ }{1-8\sin^3\frac{\alpha}{4}}[/TeX]
Application numérique : [latex]V_{20} = 1049.127335613927589991443535...[/latex] arrondi à [latex]1049.127[/latex]
Voilà !
#13 - 16-09-2013 16:59:58
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le vieux dossier de Grand-Père : N°6 (une uite de cercles?)
Question 4:
masab, on n'a pas les mêmes résultats à [latex]V_{20}[/latex]. As-tu le volume d'une sphère à [latex]V_1[/latex]?
#14 - 17-09-2013 10:52:19
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Le vieux dossieer de Grand-Père : N°6 (une suite de cercles?)
#15 - 17-09-2013 12:16:13
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le vieux dossier de Grand-Père : N°6 (une sute de cercles?)
#16 - 19-09-2013 00:27:36
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
le vieux dossizr de grand-père : n°6 (une suite de cercles?)
Pour le volume, je vais plutôt découper les sphères comme suit :
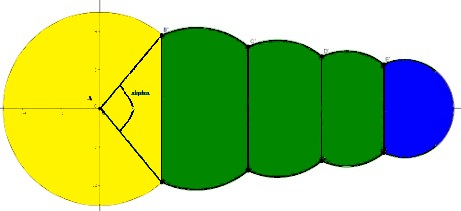
(d’ailleurs je pense que pour le calcul d'aire j'aurai dû suivre le même découpage, cela aurait probablement simplifié les calculs  ) )
Donc tous les calculs de volumes vont se résumer aux calculs de volume d'une sphère à laquelle on soustraira le volume d'une ou deux calottes sphériques.
La formule d'une calotte sphérique de hauteur [latex]h[/latex] et de rayon [latex]R[/latex] est :
[TeX]\pi R h^2 -{\pi h^3\over 3}[/latex] (1).
Dans tout ce qui suit je ferais référence à la figure suivante :
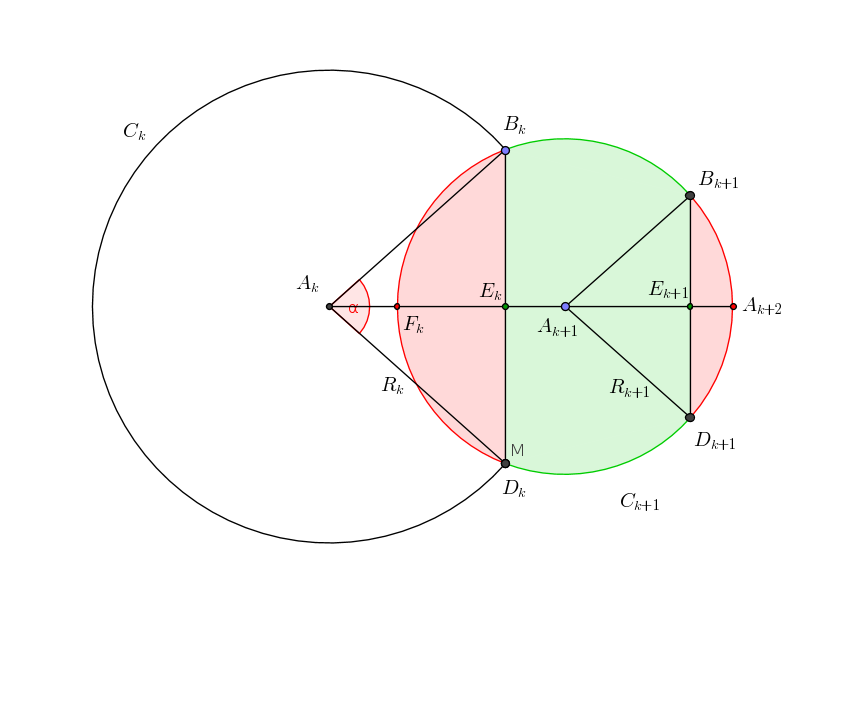
Nous savons déjà que [latex]R_{k+1} = 2R_k\sin{\alpha\over 4}[/latex].
Remarque : dans la suite j'utiliserais le résultat suivant :
[latex]1-\cos(2\theta) = 2\sin^2\theta[/TeX]
I-calcul de la distance [latex]E_kA_{k+1}[/latex] :
[TeX]E_kA_{k+1}=A_kA_{k+1} - A_kE_k = R_k - R_k\cos{\alpha\over 2} = R_k(1-\cos{\alpha\over 2})[/TeX]
autrment dit : [latex]E_kA_{k+1}=2R_k\sin^2{\alpha\over 4}[/latex].
II-calcul de la distance [latex]F_kE_k[/latex] :
[TeX]F_kE_k=F_kA_{k+1} - E_kA_{k+1}=R_{k+1} -2R_k\sin^2{\alpha\over 4}[/TeX][TeX]{\color{white}F_kE_k}=2R_k\sin{\alpha\over 4} -2R_k\sin^2{\alpha\over 4}=2R_k\sin{\alpha\over 4}(1 - \sin{\alpha\over 4})[/TeX]
Pour des raisons de clareté, dans la suite [latex]y[/latex] représentera [latex]\sin{\alpha\over 4}[/latex].
Volume Jaune :
Le volume en jaune est le volume de la première sphère moins le volume de la calotte sphérique de hauteur [latex]E_1A_2[/latex], ce qui d'après (1) et I donne :
[TeX]{4\pi\over 3}R_1^3 - \pi R_1(2R_1y^2)^2 + {\pi (2R_1y^2)^3\over 3} =[/TeX][TeX]{4\pi R_1^3\over 3}(1 - 3y^4 +2y^6)={4\pi R_1^3\over 3}(1-y)^2(1+y)^2(2y^2+1)[/TeX]
Volume Vert :
Le volume vert est composé de n-2 morceaux comme sur la figure ci-dessus.
Le calcul ci-dessus reste valable pour les autres sphères et correspond au volume "délimité" par les points [latex]B_{k+1}B_kF_kD_kD_{k+1}[/latex].
Donc le volume d'un morceau vert (que l'on va noter [latex]W_k[/latex]) est le volume ci-dessus (avec [latex]R_k[/latex] au lieu de [latex]R_1[/latex]) moins le volume de la calotte "délimitée" par les point [latex]B_kF_kD_k[/latex], c'est à dire :
[TeX]{4\pi R_k^3\over 3}(1-y)^2(1+y)^2(2y^2+1)- \pi R_k (2R_ky(1 - y))^2 +{\pi (2R_ky(1 - y)) ^3\over 3} [/TeX][TeX]= {4\pi R_k^3\over 3}[(1-y)^2(1+y)^2(2y^2+1) -3y^2(1-y)^2 + 2y^3(1-y)^3][/TeX][TeX]= {4\pi R_k^3\over 3}(1-y)^2[(1+y)^2(2y^2+1) -3y^2 + 2y^3(1-y)][/TeX][TeX]= {4\pi R_k^3\over 3}(1-y)^2(1+2y+6y^3)[/TeX]
Par le même raisonnement que pour les surfaces, on a la relations de récurrence :
[TeX]W_{k+1}=8y^3W_k[/TeX]
et donc [latex]W_k = (8y^3)^{k-2}W_2[/latex] (car ici les volumes verts commence à k=2).
donc le volume vert est égàl à [latex]W_2\sum_{k=2}^{n-1}(8y^3)^{k-2} = W_2\sum_{k=0}^{n-3}(8y^3)^k[/latex]
Volume Bleu :
Le volume en bleu est le volume de la dernière sphère moins le volume de la calotte sphérique de hauteur [latex]F_{n-1}E_{n-1}[/latex], ce qui d'après (1) et II donne :
[TeX]{4\pi\over 3}R_n^3 - \pi R_n(2R_ny(1-y))^2 + {\pi (2R_ny(1-y))^3\over 3} =[/TeX][TeX]{4\pi R_n^3\over 3}(1 - 3y^2(1-y)^2 +2y^3(1-y)^3) =[/TeX][TeX]{4\pi (8y^3)^{n-1}R_1^3\over 3}(1 - 3y^2(1-y)^2 +2y^3(1-y)^3) =[/TeX]
Volume Total:
Donc finalement le volume totale est :
[TeX]V_n={\color[rgb]{1,0.8,0} {4\pi R_1^3\over 3}(1-y)^2(1+y)^2(2y^2+1)} + [/TeX][TeX]{\color[rgb]{0,0.6,0} W_2\sum_{k=0}^{n-3}(8y^3)^k}+[/TeX][TeX]{\color{blue}{4\pi (8y^3)^{n-1}R_1^3\over 3}(1 - 3y^2(1-y)^2 +2y^3(1-y)^3)}[/TeX]
Donc si [latex]\alpha={2\pi\over 3}[/latex] alors nous avons [latex]y=1/2[/latex],
et donc :
[TeX]V_n={\color[rgb]{1,0.8,0} {4\pi R_1^3\over 3}(1/2)^2(3/2)^2(3/2)} + [/TeX][TeX]{\color[rgb]{0,0.6,0} W_2\sum_{k=0}^{n-3}1}+[/TeX][TeX]{\color{blue}{4\pi R_1^3\over 3}(1 - (3/4)(1/2)^2 +(1/4)(1/2)^3)}[/TeX]
Soit : [latex]V_n={\color[rgb]{1,0.8,0} {27\pi R_1^3\over 24}} + {\color[rgb]{0,0.6,0} (n-2)W_2}+{\color{blue}{25\pi R_1^3\over 24}} ={13\pi R_1^3\over 6}}+(n-2)W_2[/latex]
Et si [latex]\alpha\neq{2\pi\over 3}[/latex] alors [latex]8y^3\neq 1[/latex] et donc on peut appliquer la formule pour les séries géométriques, ce qui donne :
[TeX]V_n={\color[rgb]{1,0.8,0} {4\pi R_1^3\over 3}(1-y)^2(1+y)^2(2y^2+1)} + [/TeX][TeX]{\color[rgb]{0,0.6,0} W_2{1-(8y^3)^{n-2}\over 1-(8y^3)}}+[/TeX][TeX]{\color{blue}{4\pi (8y^3)^{n-1}R_1^3\over 3}(1 - 3y^2(1-y)^2 +2y^3(1-y)^3)}[/TeX]
Vérification numérique :
[TeX]y = \sin{5\pi\over 36}[/TeX][TeX]{4\pi R_1^3\over 3} ={500\pi \over 3} \simeq 523,598776[/TeX][TeX](1-y)^2(1+y)^2(2y^2+1)\simeq 0,9156946[/TeX]
=====> Volume Jaune [latex]\simeq 479,45658[/latex]
[TeX](8y^3)^{19}(1 - 3y^2(1-y)^2 +2y^3(1-y)^3)\simeq 0.00005853[/TeX]
=====> Volume Bleu [latex]\simeq 0,0306478[/latex]
[TeX]{1-(8y^3)^{18}\over 1-(8y^3)}\simeq 2.524059[/TeX][TeX]8y^3(1-y)^2(1+2y+6y^3)\simeq 0.46263175 [/TeX][TeX]W_2={4\pi (8y^3)R_1^3\over 3}(1-y)^2(1+2y+6y^3)\simeq 242,2334[/TeX]
=====> Volume Vert [latex]\simeq 611,411442[/latex]
=====> [latex]V_{20}\simeq 1090,899[/latex]
Voilà, j'espère que je n'ai pas fait d'erreurs de calculs.
J'ai fait quelques recherches sur internet, et je suis tombé sur un théorème appelé théorème de Guldin. Mais pour utiliser ce théorème, il faut savoir où se trouve le centre de gravité de la figure, et apparemment ça à l'air plus difficile que de calculer directement le volume, dommage... (c'aurait été classe  ) )
Il y a sûrement plus simple.
#17 - 19-09-2013 10:26:29
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
le vieux dossier de grand-père : n°6 (une siite de cercles?)
cogito: que du plaisir à te lire. Dans le calcul de [latex]W_k[/latex], j'ai l'impression que que tu n'as pas soustrait 2 calottes mais une seule. Je pense la différence des résultats à [latex]V_{20}[/latex] doit provenir de là. Vérifie voir. Merci pour cette débauche d'énergie 
Pour le théorème de Guldin, j'avais pensé à cela en posant cette question mais au moment de le faire, je ne suis très rapidement rendu compte le rayon de gravité est plus difficile à déterminer que ce que je pensais.
#18 - 19-09-2013 16:03:16
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
Le vieux dssier de Grand-Père : N°6 (une suite de cercles?)
En visionnant les réponses de cogito, je crois qu'on peut lui décerner la palme du latex d'or !
 
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#19 - 19-09-2013 17:59:14
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Le vieux dossier de Grand-Père : N°6 (une suite de cercless?)
J'étais parti comme cogito, mais après je me suis perdu dans les calculs sans pouvoir finir. Bravo à cogito.
Edit: Et bravo à masab aussi bien sur.
#20 - 19-09-2013 19:52:00
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
le vieux dossier de granf-père : n°6 (une suite de cercles?)
Il y a sûrement plus simple.
#21 - 19-09-2013 20:42:42
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Le vieux dossier de Gran-Père : N°6 (une suite de cercles?)
Merci à tous et un tableau d'honneur à masab et cogito
Je pose ci dessous ma solution.
#22 - 19-09-2013 22:29:39
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
le vieux dossier de grand-pèrr : n°6 (une suite de cercles?)
Proposition de solution:

Préliminaires:
[TeX]\alpha[/latex] est noté a et [latex]\beta[/latex] b sur la figure.
[latex]AA_i=AB=R=R_1[/latex] et [latex]A_iB=R_i[/TeX]
D'après Al-Kashi, [latex]R_i^2=R^2+R^2-2*R*R*cos(\alpha/2)[/latex]
soit [latex]R_i=2*R*sin(\alpha/4)[/latex] puisque [latex]1-cos(t)=sin(t/2)^2[/latex] quelque soit t.
On en conclut que [latex]R_i[/latex] est une suite géométrique de raison [latex]q=2*sin(\alpha/4)[/latex].
[TeX]R_i=R*q^i.[/TeX]
1-) Aire totale
Désignons par [latex]F_1[/latex] l'aire du [latex]1^{ier}[/latex] cercle, par [latex]F_n[/latex] celle du dernier, par [latex]f_i[/latex] celle d'un cercle intermédiaire de rang i et par [latex]F_i[/latex] l'aire totale des cercles intermédiaires (de rang 2 à n-1).
[TeX]F_1=\pi*R^2-\frac{R^2}{2}*(\alpha-sin(\alpha))=R^2*(\pi-\alpha/2+sin(\alpha)/2))[/TeX]
De la même manière:
[TeX]F_n=R_n^2*(\pi-\beta+sin(2*\beta)/2))=R^2*q^{2n}*(\pi-\beta/2+sin(2*\beta)/2)) où \beta=(2*\pi-\alpha)/4.[/TeX][TeX]f_i=R^2*q^{2i}*(\pi-\beta+sin(2*\beta)/2)-\alpha/2+sin(\alpha)/2))=R^2*q_s^n*K_s[/latex] où
[latex]K_s=(\pi-\beta+sin(2*\beta)/2)-\alpha/2+sin(\alpha)/2))=constante[/latex] et
[latex]q_s=q^2[/latex].
[latex]f_i[/latex] est une suite géométrique de raison [latex]q_s[/latex].
[latex]F_i=\sum_{j=2}^{j=n-1}f_i=f_2*\frac{1-q_s^{n-2}}{1-q_s}[/TeX][TeX]S_n=F_1+F_n+F_i[/TeX][TeX]S_n=R^2*(\pi-\alpha/2+sin(\alpha)/2))+R^2*q^{2n}*(\pi-\beta+sin(2*\beta)/2))+f_2*\frac{1-q_s^{n-2}}{1-q_s}[/TeX]
2-) Etude convergence
Le comportement de [latex]S_n[/latex] à l'infini est le même que celui de [latex]F_i[/latex] car [latex]F_1[/latex] et [latex]F_n[/latex] sont des constantes.
[TeX]q_s=4*sin(\alpha/4)^2[/TeX]
Si [latex]q_s>1[/latex] c'est à dire [latex]\alpha>2\pi/3[/latex] alors [latex]F_i[/latex] est divergente et [latex]S_n[/latex] l'est aussi.
Si [latex]q_s=1[/latex] c'est à dire [latex]\alpha=2\pi/3[/latex] alors tous les cercles ont le même rayon R, [latex]F_i[/latex] et [latex]S_n[/latex] sont divergentes.
Si [latex]q_s<1[/latex] c'est à dire [latex]\alpha<2\pi/3[/latex] alors [latex]F_i[/latex] et [latex]S_n[/latex] sont convergentes et dans ce cas
[TeX]S=R^2*(\pi-\alpha/2+sin(\alpha)/2))+f_2*\frac{1}{1-q_s}[/TeX]
3-) AN
[TeX]\alpha=\frac{5*\pi}{9}[/latex], R=5 et n=20
[latex]q=2*sin(\alpha/4)=0.84523652[/TeX]
[TeX]q_s=q^2=0.71442478[/TeX]
[TeX]F_1=69.0332976[/TeX]
[TeX]F_{20}=0.100355[/TeX]
[TeX]f_2=35.89788256[/TeX]
[TeX]F_i=125.4082676[/TeX][TeX]S_{20}=194.542[/TeX]
4-) Calcul du volume [latex]V_n[/latex]
Pour calcul le volume, j'ai procédé comme pour la surface. Les 2 volumes d'extrémités sont calculés puis ceux des corps intermédiaires.
Désignons par [latex]G_1[/latex] le volume de la première boule (sans la calotte [latex]BDA_i[/latex]), [latex]G_n[/latex] celui de la boule n (sans la calotte [latex]B_nD_nA_n[/latex]) et [latex]g_i[/latex] celui de la boule intermédiaire de rang i (sans les 2 calottes "découpées").
[TeX]OA_i=R*(1-cos(\alpha/2))[/latex] (hauteur de la calotte)
[latex]G_1=\frac{4*\pi*R^3}{3}-\frac{\pi*OA_i^2}{3}*(3*R-AO_i)[/TeX]
soit
[TeX]G_1=\frac{\pi}{3}*R^3*(2+3*cos(\alpha/2)-cos(\alpha/2)^3)[/TeX]
Par analogie pour la dernière boule:
[TeX]G_n=\frac{\pi}{3}*R_n^3*(2+3*cos(\beta)-cos(\beta)^3)[/TeX]
Pour le calcul du volume d'une boule intermédiaire de rang i. Deux calottes sont enlevées de la boule sphérique, leurs hauteurs sont:
[TeX]h_g=R_i*(1-cos(\beta))[/latex] (hauteur de la calotte à gauche)
[latex]h_d=R_i*(1-cos(\alpha/2))[/latex] (hauteur de la calotte à droite)
[latex]g_i=\frac{4*\pi*R^3}{3}-\frac{\pi*h_g^2}{3}*(3*R_i-h_g)-\frac{\pi*h_d^2}{3}*(3*R_i-h_d)[/TeX]
soit
[TeX]g_i=K_v*R_i^3[/latex] où
[latex]K_v=\frac{\pi}{3}*[3*cos(\alpha/2)+3*cos(\beta)-cos(\alpha/2)^3-cos(\beta)^3]=constante[/TeX]
On remarque que [latex]g_i[/latex] est une suite géométrique de raison [latex]q_v=q^3=8*sin(\alpha/4)^3[/latex].
[TeX]G_i=\sum_{j=2}^{j=n-1}g_i=g_2*\frac{1-q_v^{n-2}}{1-q_v}[/TeX][TeX]V_n=G_ 1+G_n+G_i[/TeX][TeX]V_n=\frac{\pi}{3}*R^3*[2+3*cos(\alpha/2)-cos(\alpha/2)^3]+\frac{\pi}{3}*R_n^3*[2+3*cos(\beta)-cos(\beta)^3]+[/TeX]
[TeX]g_2*\frac{1-q_v^{n-2}}{1-q_v}[/TeX]
Comme pour la surface, lorsque [latex]\alpha[/latex] est inférieur à [latex]2\pi/3[/latex], [latex]G_i[/latex] est convergente donc [latex]V_n[/latex] l'est aussi. Soit V la limite de [latex]V_n[/latex] dans ce cas.
[TeX]V=\frac{\pi}{3}*R^3*(2+3*cos(\alpha/2)-cos(\alpha/2)^3)+g_2*\frac{1}{1-q_v}[/TeX]
AN pour R=5, [latex]\alpha=5*\pi/9[/latex] et n=20
[TeX]G_1=479.456581[/TeX]
[TeX]G_{20}=0.02876158[/TeX]
[TeX]K_v=2.989907155[/TeX]
[TeX]g_2=225.684888[/TeX]
[TeX]G_i=569.6419931[/TeX][TeX]V_{20}=1049.127[/TeX]
#23 - 19-09-2013 22:54:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Le vieux dossier de Grand-Père : N°6 (une suite de cercls?)
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum