Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 01-10-2010 01:08:41
cercles rangents à des cerclesVoici une énigme qui fera plaisir aux géomètres parmi vous. Elle n'est pas de moi : je vous donnerai le lien en guise de réponse
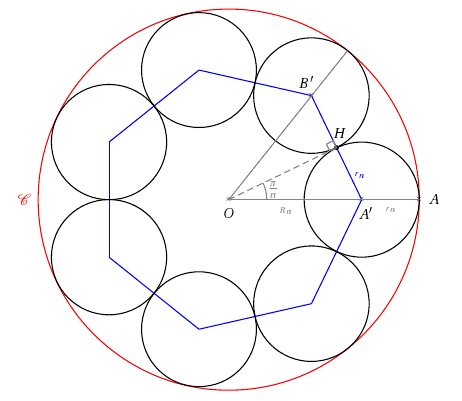
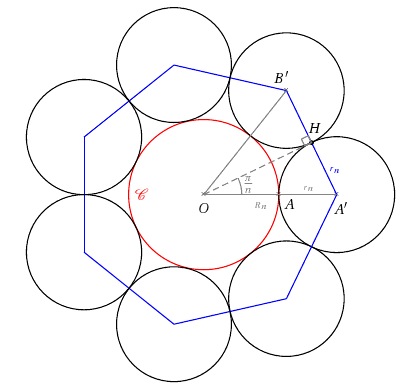
Je mets les figures d'illustration (pour n=7) en spoiler, car elles donnent un modus operandi pour la résolution Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#0 Pub#2 - 01-10-2010 10:21:19
Cercles tangents à des ecrclesBonjour Mathias, J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit. #3 - 01-10-2010 10:27:35
Cercles tangentts à des cerclesAlors je me lance sans regarder les spoilers (a ce propos la technique de vasimolo qui consiste a placer les spoilers progressivement et non des le debut est pas mal #4 - 01-10-2010 12:09:00
cercles tangents à des cerckesKlimrod et McFlambi ont tous deux répondu d'instinct à la question "finale" sans même faire le reste des calculs avant... Je suis hautement impressionné, messieurs Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #5 - 01-10-2010 17:48:04
Cercles tangents à des cercleesAu pif je dirais bien entendu PI puisque si les cercles deviennent infiniment petits le polygone composé de leurs centres se confondra avec la circonférence du cercle donc 2PI ( et comme un coté fait pas loin du diamètre ? ) #6 - 01-10-2010 20:15:56
Cercles tangentts à des cercles[TeX]\lim_{n\to +\infty}{nr_n} = \frac{1}{2} \time[ \lim_{n\to +\infty}{nD_n}]=\pi/2[/TeX] The proof of the pudding is in the eating. #7 - 01-10-2010 21:04:05
Cercles tangents à des ecrclesIntuitivement, je ferais tendre les deux valeurs vers pi. #8 - 02-10-2010 01:07:14
cercles rangents à des cerclesDans les deux cas, le périmètre du polygone régulier est [latex]2nr_n[/latex]. Quand n tend vers l'infini, le polygone tend vers le cercle de rayon 1. Donc [latex]nr_n[/latex] tend vers [latex]\pi[/latex]. #9 - 02-10-2010 11:11:07
Cerrcles tangents à des cerclesBonjour à tous #10 - 02-10-2010 12:01:53#11 - 02-10-2010 13:01:54
cerckes tangents à des cerclesN'oubliez pas qu'on demande aussi de calculer [latex]r_n[/latex] dans chacun des deux cas Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #12 - 04-10-2010 11:25:11
Cercles tangent sà des cercles1er cas #13 - 04-10-2010 16:02:10
cerclzs tangents à des cerclesAu feeling pour la case réponse: les cercles vont devenir de plus en plus petits pour au final "coller" au premier cercle. Comme n*2*Rn correspond au périmètre du polygone qui parcourt tous les centres de cercles, il tend en théorie vers 2Pi (le périmètre du cercle principal, qu'on "colle" comme expliqué ci dessus). "Pi" devrait donc valider la case réponse (et le valide effectivement). #14 - 04-10-2010 22:53:39
Cercles tangents àà des cerclesOh, tiens, je retrouve sensiblement les mêmes que dans mon autre énigme, que je viens de clôturer Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.