Pour moi c'est une évidence , chaque composante connexe impose sa direction les autres sont libres , après , on peut pinailler à l'infini


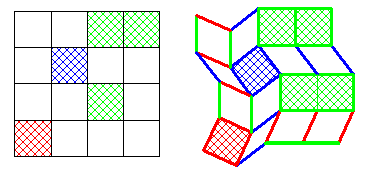
Vasimolo

Tu as raison, mon raisonnement n’était pas clair.

En fait je ne cherche pas à construire les treillis de façon récursive : (n,p) rigide n’impose clairement pas que ses ‘sous-treillis’ (n-1,p) soit rigides.
Je dis juste que la règle n+p-1 marche pour les ‘petits’ treillis, et que si on arrive à battre cette règle à partir d’une certaine taille, le plus petit qui bat la règle a autant ou moins de cellules rigidifiées que le minimum possible de tout treillis (n-1,p) ou (n,p-1) rigides. Et que ça amène un pb. Et c’est là où je ne suis pas clair. Je reprends…

Imaginons que (n,p) est le plus petit treillis battant la règle n+p-1 : Il est donc rigide avec au plus n+p-2 cellules rigidifiées.
Toutes ses lignes et toutes ses colonnes ont au moins une cellule rigide (sinon cisaillement possible). Donc aucun sous-treillis (n-1,p) ou (n,p-1) obtenu en supprimant une ligne ou une colonne quelconque (et en ‘recollant’ si ce n’est pas un bord) n’est rigide, car il ne contient plus que n+p-3 cellules rigidifiées max. De fait toute ligne ou colonne est structurelle pour le treillis (n,p).

Prenons une de ces lignes au hasard. Sans elle, le sous treillis ‘recollé’ n’est pas rigide. Avec elle, le treillis l’est devenu. Donc la ligne ajoutée fait mieux que les lignes de bord des sous-treillis pour transmettre la rigidité à l’ensemble.
Si la ligne ajoutée ne contenait qu’une cellule rigidifiée, elle ferait au mieux aussi bien que chacun des bords des sous-treillis précédents (qui ne peuvent avoir 0 cellule rigidifiée, sinon cisaillement inévitable). Ie il suffirait pour l’un des 2 sous-treillis de choisir de localiser la cellule rigidifiée à la même position que celle de la ligne ajoutée, et le résultat serait identique : le sous-treillis (n-1,p) serait aussi rigide que le treillis (n,p). Et on aurait donc un sous-treillis (n-1,p) rigide avec seulement n+p-3 cellules rigides, ce qui est impossible. Donc la ligne ajoutée ne peut contenir ni 0 ni 1 seule cellule rigidifiée. Elle en contient à minima 2. Le raisonnement marche aussi si la ligne ôtée est au bord.
Si toute ligne et toute colonne du treillis contient à minima 2 cellules rigidifiées, le nombre total de ces cellules est égal à max(2n, 2p). Mais max(2n, 2p)>n+p-1, ce qui contredit notre hypothèse.
On ne peut trouver de plus petit treillis battant la règle n+p-1.

Toufau
Spoiler : [Afficher le message] "Et on aurait donc un sous-treillis (n-1,p) rigide avec seulement n+p-2 cellules rigides, ce qui est impossible"
n-1 + p - 1 = n+p-2
D'après ce que tu cherches à démontrer, c'est possible de rigidifier un treillis (n-1,p) avec n+p-2.
Si tu essayes de résoudre par récurrence, il faudrait que tu montres que l'on peut rendre le sous treillis rigide sans ajouter de cellules (mais en en déplacant). Ici, tu en ajoutes une, donc ça ne t'apprend rien.

"Ie il suffirait pour l’un des 2 sous-treillis de choisir de localiser la cellule rigidifiée à la même position que celle de la ligne ajoutée, et le résultat serait identique : le sous-treillis (n-1,p) serait aussi rigide que le treillis (n,p)."
Pourquoi est-ce vrai? (C'est vrai, ça peut se démontrer directement, via un argument déjà amené par les autres p2tiens, mais ça n'est pas une propriété si évidente)

Si tu arrives à mener cette preuve à bien, tu auras trouvé une preuve différente de celle trouvée par tout les autres (qui ont tous la même que moi), mais je ne sais pas si on peut mener à bien l'approche par récurrence directement, c'est à dire sans donner pour le prouver une construction qui marche directement....


nodgim
Oui, je modifie.

Vasimolo m'a donné un exemple à 3 réseaux. J'ai du mal à évaluer à quel point cette construction est évidente (mais si on voit bien l'idée, personnellement, comme ça, je ne l'ai pas trouvée 100% évidente) mais il est vrai que l'évidence reste assez subjective. Personnellement, j'ai une construction plus évidente (où on ne se base que sur un seul des réseaux), ce qui permet de clore la preuve vraiment rigoureusement, mais si vous juger que votre construction est suffisamment évidente, je ne vous jetterais pas la pierre...

Caduk, le 'n+p-2' était une erreur... n+p-2-1=n+p-3! (corrigé dans le post précédent)

Concernant le "Ie il suffirait pour l’un des 2 sous-treillis de choisir de localiser...", je comprends ta remarque.
J'utilise un autre argument (que je n'avais pas exprimé, bêtement) : Une ligne de bord qui ne possède qu'une cellule rigidifiée n'aura pas plus de cellules rigides - et au même endroit - que la ligne sur laquelle elle s'appuie. Au mieux, si la cellule rigidifiée s'appuie elle même sur une cellule rigide de la ligne précédente, elle propage cette rigidité (en créant un 'L' ou un 'T') sur sa ligne, pour toute cellule contiguë et en regard d'une cellule rigide de la ligne précédente.
Si toutes les cellules rigides de la ligne précédente étaient elles-mêmes contiguës, on obtient la même ligne, pas mieux.
De fait, l'utiliser pour réunir deux treillis non rigides ne sert à rien pour rigidifier l'ensemble. Pas plus en tout cas que si elle n'avait pas été là. Si l'ensemble n'était pas rigide sans elle, il ne le sera pas plus avec.
C'était globalement le sens de mon raisonnement, décidément pas hyper clair :-)

Caduk,

Sur ton premier point
Ce que je dis : je prends un treillis (n,p) contenant n+p-2 cellules rigidifiées (mon hypothèse à ‘casser’), et j’enlève une ligne ou une colonne contenant 1 cellule rigidifiée => le sous treillis (n-1,p) ou (n,p-1) reconstitué va contenir exactement n+p-3 cellules rigidifiées.

Sur ton second point
Je suis d’accord, la rigidité ne se propage pas que par proximité immédiate à l’intérieur d’un treillis. C’est même vrai pour la majorité des treillis rigides.

La rigidité se propage par contre par contact direct d'une ligne de bord si celles-ci ne contient qu’une unique cellule rigidifiée : il ne pourra pas y avoir de cellule de cette ligne de bord qui devienne rigide sans être au contact elle-même d’une cellule rigide de la ligne précédente (ie d’une cellule qui aurait déjà été rigide sans cette ligne de bord complémentaire).
Donc en ajoutant une ligne avec une unique cellule rigidifiée entre deux sous-treillis qui, réunis, ne formaient pas un treillis rigide, on n’obtiendra pas plus un treillis rigide :
-    soit la cellule rigidifiée de notre ligne intercalaire est en regard d’une cellule rigide d’un des sous-treillis qu’on cherche à réunir, et elle reproduira au mieux la même ligne que ce sous-treillis, sans aucun apport à l’ensemble de fait. Pas rigide sans, pas rigide avec...
-    Soit la cellule rigidifiée de la ligne intercalaire n’est au regard d’aucune cellule rigide des deux sous-treillis. Dans ce cas, même rigide elle-même, elle n’est pas figée : elle peut toujours pivoter faute d’être tenue figée par ses cellules de contact. Et aucune des cellules de sa ligne n’est rigide car elle ne transmet pas la rigidité sur sa ligne (quand bien même d'ailleurs toutes les autres cellules des deux bords des sous-treillis étaient rigides : pas de L ni de T pour transmettre la rigidité).
Ce qui, dans mon raisonnement, permettait de conclure à l’impossibilité d’un treillis (n,p) rigide avec seulement n+p-2 cellules: on ne peut, en ajoutant une ligne avec une unique cellule rigidifiée à un treillis (n-1,p) non rigide, obtenir un treillis (n,p) rigide.

Bon d’un autre côté, si je n’avais pas été clair dans mes posts précédents, celui-ci n’y changera sans doute rien 😊

Oui Caduk , c'est une façon de voir les choses .

Nous avons chacun notre perception de ce qui est clair ou pas . Personnellement j'ai aussi beaucoup de mal à suivre les réponses traînant un paquet de sous-entendus censés être évident . Mais comme j'ai aussi ce défaut ...

Joli problème en tout cas

Vasimolo