|
#1 - 02-12-2015 18:19:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#2 - 02-12-2015 18:32:32
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gteau 111
Salut Vasimolo,
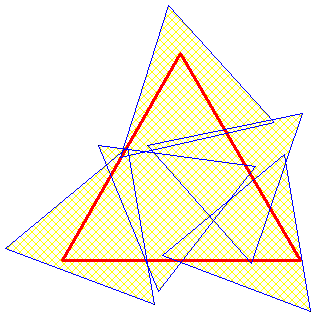
On recouvre exactement un grand triangle avec 4 petits. Si ces petits sont une taille légèrement plus faible, avec 5 d'entre eux je ne vois comment remplir le grand triangle. Aussi, il me semble que 4 triangles des 5 qui recouvrent ton triangle rouge le couvrent également.
Si tant est que les petits triangles sont des équilatéraux comme sur le dessin.
#3 - 02-12-2015 18:40:56
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 11
Oui , Nodgim les triangles bleus sont bien équilatéraux . Pour la suite le : "il me semble" , mériterait quelques justifications 
Vasimolo
#4 - 02-12-2015 19:20:00
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteeau 111
Il faudra bien remplir les 3 sommets du grand triangle avec 3 petits triangles. Restera alors à remplir le milieu avec, au pire, 1 triangle de coté légèrement supérieur à celui des petits triangles. Or un triangle de coté légèrement plus petit ne peut couvir plus d'un sommet. Les 2 triangles ne pourront donc au mieux couvrir que 2 sommets.
#5 - 02-12-2015 19:27:29
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
gâreau 111
La taille minimum recouvrable à coup sûr, ça aurait un sens mais la taille maximum... euh je ne vois pas le problème vu qu'il n'y a pas de limite à la taille des triangles bleus tel que le problème est posé.
#6 - 02-12-2015 19:43:38
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
gâyeau 111
Salut !
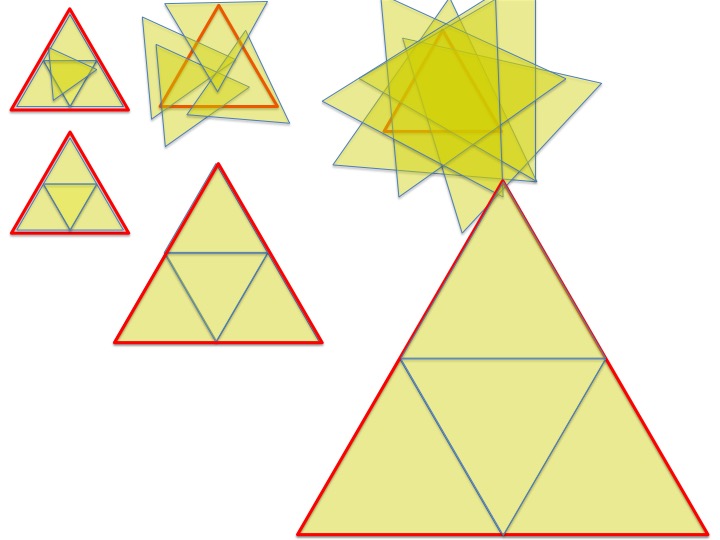
En dessinant un triangle équilatéral et en reliant tous les milieux des côtés on dessine 4 triangles équilatéraux égaux.
Je dirait donc un triangle de côté 2 fois le côté d'un triangle bleu...
#7 - 03-12-2015 09:46:39
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
#8 - 03-12-2015 10:07:03
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
âteau 111
Le problème semble sympa mais je ne comprend pas précisément l'énoncé. Faut il se fier au dessin ?
Le problème est il : a partir de 4 triangles équilatéraux de même taille l, quelle taille maximum L pour un triangle équilatéral peut on recouvrir ?
#9 - 03-12-2015 11:27:34
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Gâteau 1111
bonjour.
4 , 5 , 6 , 7 biscuits : même combat pour un triangle équilatéral de côté 20 cm. il me semble. si le biscuit a pour côté a 4 biscuits suffisent pour couvrir un triangle de côtés 2a . Pour un triangle légèrement plus grand (2a + un chouia ) , 4 biscuits supplémentaires sont nécessaires il me semble .
donc avec 4 biscuits on couvre toujours ce triangle de 20cm d'arête ; dès lors que
le côté du biscuit est 10cm <= c < 20cm
#10 - 03-12-2015 12:37:46
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâetau 111
Autre idée: pour recouvrir 1 coté du triangle, il faut 3 petits triangles. Pour les 2 cotés il en faut 5. Le 3ème coté n'est pas couvert.
#11 - 03-12-2015 23:19:00
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 11
Je regarde en détail les solutions proposées .
En attendant je précise la question qui n'était pas franchement limpide ( comme d'habitude  ) . ) .
On sait qu'on peut recouvrir complètement le triangle rouge avec les 5 biscuits bleus . On ne connait pas la taille des biscuits bleus ni leurs dispositions , on sait simplement que ce sont des triangles équilatéraux , qu'ils ont la même taille et qu'ils recouvrent complètement le triangle rouge . On se demande quelle est la taille du plus grand triangle équilatéral qu'on est assuré de pouvoir recouvrir avec seulement 4 de ces biscuits .
J'espère que c'est plus clair , sinon n'hésitez pas à poser des questions .
Vasimolo
#12 - 03-12-2015 23:32:42
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteai 111
@Nodgim : c'est bon 
@Gwen : j'ai essayé de répondre à tes questions dans le message précédent .
@Golgot & @Nobodydy : c'est juste mais on ne connait pas le côté du triangle bleu .
@Portugal : pas tout à fait , j'espère que le message précédent clarifie le problème .
@Unecoudée : peut-être mais il faut justifier 
Vasimolo
#13 - 03-12-2015 23:34:27
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Gâteau 1111
Dans ce cas mon intuition :
Un triangle (toujours équilatéral par la suite) se divise facilement en 4 petits triangles
Supposons notre triangle "rempli de la sorte et ajoutons un 5eme triangle a placer.
* on peut toujours la placer de coté et couvrir la même surface donc C<=20
* au mieux on couvrira parfaitement le triangle agrandi et donc C>= 4 / 5 * 20=16
Cependant,"il semble" que pour agrandir le triangle il faut commencer par "baiser les 3 petits triangles pour couvrir le base d'un triangle agrandi. Mais dans ca cas, il est impossible de couvrir le haut de notre nouveau triangle.
Mon intuition me fait donc répondre 20cm... (pas facile d'expliquer quand on ne sait pas poster un dessin...)
#14 - 03-12-2015 23:41:23
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâreau 111
Ton intuition est la bonne , il y a une justification simple qui peut se passer d'illustration .
Vasimolo
#15 - 03-12-2015 23:46:34
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Gâteua 111
J'y pensais.
On prend notre triangle agrandi vers le bas.
On doit couvrir les 3 sommets. autant les faire aller ' a l'intérieur du triangle" tant que se faire.
Il faut bien alors remplir le point en base au milieu donc on palce un 4eme triangle qui "remonte" au mieux tant qu'à faire mais il nous reste alors une figure restante en forme de trapeze que l'on ne peut clairement pas remplir avec 1 triangle vu que dan le sens de la largeur il est "en dessous" du petit triangle du haut donc plus large...ce qui n'est pas possible
#16 - 03-12-2015 23:53:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
GGâteau 111
Là il faudrait une illustration 
Vasimolo
#17 - 04-12-2015 00:04:21
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
Gâteaau 111
http://www.prise2tete.fr/upload/portugal-triangle_1.pdf
Voici avec mon écriture et un stylo qui rend l’âme...
en m'excusant pour le torticolis...
C'est un peu à la manière d'une énigme...Les 3 premiers sommets font trouver les 3 premiers triangles qui font apparaître un autre sommet donc un nouveau triangle et laissent apparaître un trapèze non atteignable...
Il y a une petite erreur dans le dessin du triangle qui ne change pas le raisonnement. Réponse plus concise plus loin dans la page...
#18 - 04-12-2015 00:14:24
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 11
Tu as l'idée , mais on peut faire plus simple 
Vasimolo
#19 - 04-12-2015 07:19:15
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
âGteau 111
Si les triangles bleus faisaient moins de 10 cm de côté, il en faudrait 6 pour couvrir le triangle rouge puisque les trois sommets et les 3 milieux des côtés s'excluraient mutuellement au recouvrement. Donc les triangles ont au minimum 10 cm de côté.
Avec 4, on est dons assurés de recouvrir le triangle rouge.
#20 - 04-12-2015 11:41:47
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
#21 - 04-12-2015 17:16:18
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 11
@Gwen : c'est ça .
@Nobodydy : je ne sais plus comment expliquer autrement , j'essaie quand même sans conviction 
On oublie tout ce que j'ai dit et :
J'ai à ma disposition un lot de 5 petits triangles équilatéraux identiques . Avec ces 5 triangles je peux recouvrir complètement un triangle équilatéral de côté 20 cm . Maintenant je ne prends plus que 4 des 5 triangles . L'aire de ces triangles représente au moins les 4/5 de l'aire du grand triangle initial , on va donc pouvoir , en les assemblant comme tu l'as fait , construire un triangle dont l'aire sera au moins égale aux 4/5 de celle du grand triangle . On est donc certain avec eux de pouvoir recouvrir un triangle de côté [latex]8\sqrt{5}\approx 17,88...[/latex] .
Sans connaître la taille des 4 petits triangles , peux-tu être assuré qu'ils peuvent recouvrir un triangle encore plus grand et jusqu'à quelle limite ???
Vasimolo
#22 - 04-12-2015 17:26:16
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
âGteau 111
Une explication sans dessin
Soit un triangle ABC de dimension x recouvert complètement par 4 petits triangles de cotés x/2 par la construction élémentaire du recouvrement parfait
Considérons maintenant un triangle AB'C' de dimension x+€ ou B' et C' sont placés dans le prolongement de AB et AC.
Appelons A'', B'', C'' les milieux respectifs de B'C', AC', AB'
Pour recouvrir AB'C' il faut entre autres recouvrir les points A, B', C', A'', B'', C"
Or aucun triangle de longueur x/2 ne peut toucher 2 de ces points qui sont tous séparés d'au moins de (x+€)/2.
Cinq triangles x/2 ne peuvent donc pas recouvrir notre nouvelle figure.
#23 - 04-12-2015 17:30:27
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
âteau 111
C'est ça Portugal 
Vasimolo
#24 - 04-12-2015 17:33:36
- portugal
- Professionnel de Prise2Tete
- Enigmes résolues : 22
- Messages : 382
GGâteau 111
C'est toujours bien de se pousser à décrire exactement quelque chose dont on a l'idée approximative...c'est l'attrait de ce forum interactif qui me pousse dans mes retranchements...un grand merci !
#25 - 04-12-2015 17:51:51
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
|
 |

 Accueil
Accueil
 Forum
Forum