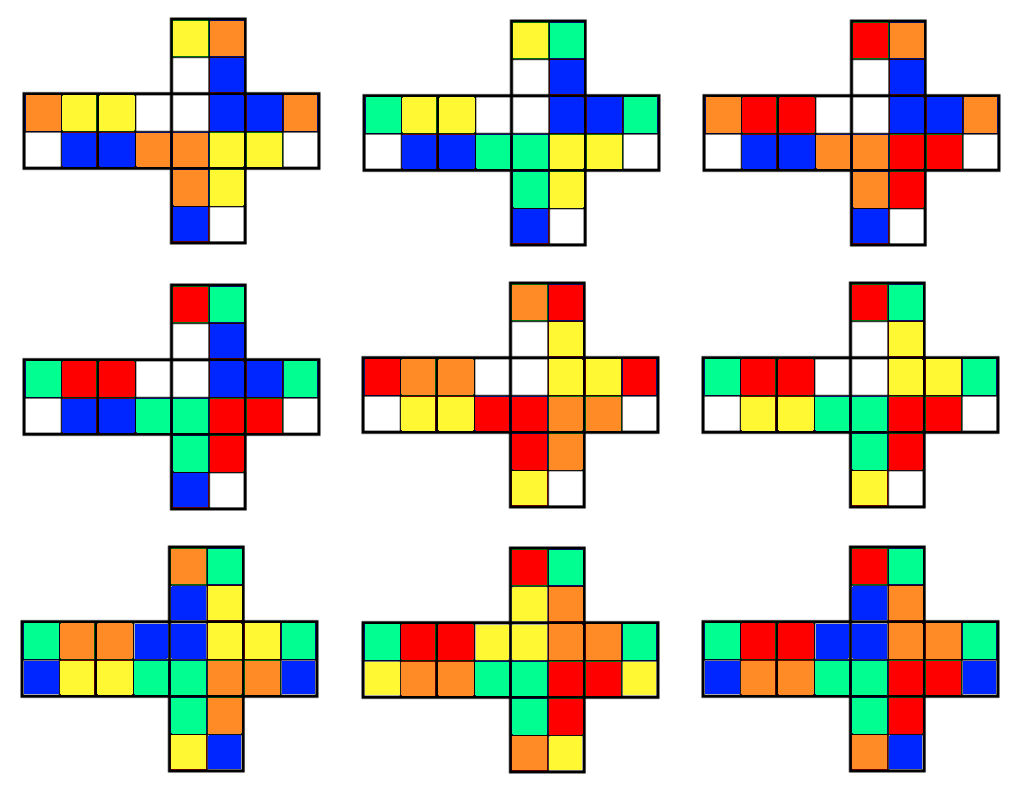|
#1 - 19-01-2021 19:45:01
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
Sudoku en couleeur
Sachant sans doute que j'aimais bien me prendre la tête, on m'a offert pour Noël un "Color cube Sudoku".

Il s'agit d'un jeu de réflexion composé d'une boîte dans laquelle il faut disposer 9 cubes. Chaque cube comporte quatre couleurs parmi six :
Blanc (W), Bleu, Jaune, Orange, Rouge et Vert.
Les deux sommets opposés sont de même couleur. Chaque face offre donc à la vue quatre couleurs. La disposition des couleurs est différente sur chaque face.
Les neuf cubes présents dans la boîte combinent les couleurs :
WBJO, WBJV, WBRO, WBRV, WJOR, WJRV, BJOV, JORV et BORV.
Par exemple, le développement du cube WBRV donnerait ceci :
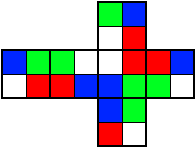
Le but du jeu est de remplir la boîte en respectant la règle du sudoku : les six couleurs doivent apparaître dans chacune des six lignes et des six colonnes (on ne doit donc pas rencontrer deux fois une même couleur dans une ligne ou une colonne).
Les habitués des Énigmes Mathématiques devant se sentir un peu frustrés actuellement, je vous propose un peu d'analyse combinatoire :
A) On peut trouver sur Internet qu'avec ces couleurs, on peut afficher sur la face supérieure de la boîte plus de 2 milliards arrangements. Pourrait-on avoir un nombre plus précis ?
B) Parmi tous les arrangements, on prétend par ailleurs qu'il existe plus de 500 000 solutions compatibles avec les règles du Sudoku. Quel en est le nombre exact ?
C) A partir d'une solution respectant les règles du Sudoku, combien de solutions différentes peut-on obtenir par combinaisons de rotations, de permutations entre les lignes ou les colonnes et de symétries éventuelles ?
D) Combien de cubes différents peut-on fabriquer à partir de ces six couleurs, en respectant la règle de la disposition différente des couleurs sur chaque face ?
E) A partir de ces N cubes, combien de arrangements existe-t-il pour remplir la boîte de 9 cubes ?
F) Parmi ces arrangements, combien de solutions respectent la règle du Sudoku ?
Je ne prétends pas connaître toutes les réponses, notamment celles sur les solutions respectant la règle du Sudoku  . .
Amusez-vous bien. Mais vous n'êtes pas obligés d'attendre d'avoir calculé les réponses à toutes les questions pour proposer les résultats de vos cogitations  . .
#2 - 21-01-2021 13:12:56
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
sudoky en couleur
Bonjour,
Jackv a écrit:Les neuf cubes présents dans la boîte combinent les couleurs :
WBJO, WBJV, WBRO, WBRV, WJOR, WJRV, BJOV, BJOV et BORV.
Il y a 2 cubes identiques. Si l'on en croit la photo, n'est-ce pas plutôt ?
WBJO, WBJV, WBRO, WBRV, WJOR, WJRV, BJOV, JORV et BORV
#3 - 21-01-2021 15:22:00
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
sudoku rn couleur
Merci à enigmatus qui me signale une coquille :
Il y a 2 cubes identiques. Si l'on en croit la photo, n'est-ce pas plutôt ?
WBJO, WBJV, WBRO, WBRV, WJOR, WJRV, BJOV, JORV et BORV
Bon sang, mais c'est bien sûr !
J'espère que ce n'est pas cette petite erreur du texte qui vous a empêché de vous lancer dans les calculs  ? ?
Le texte est corrigé  . .
#4 - 21-01-2021 16:22:07
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Sudoku en couelur
Je me lance (doucement)…
Question A :
Plus de 2 milliards, d'accord, mais c'est une sacrée approximation…
Voici ce que je trouve :
- nombre de façons de choisir les emplacements des 9 cubes dans la boîte : 9!
- chaque cube peut être orienté de 24 façons différentes : 6 faces × 4 orientations par face
- ce qui fait 24**9 façons d'orienter les 9 cubes, sans tenir compte de leur position dans la boîte
Soit un total de 9! * 24**9 = 958659120196485120 possibilités (environ 0.959e18)
#5 - 21-01-2021 18:29:02
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
#6 - 21-01-2021 19:01:01
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
dudoku en couleur
Pour chaque cube, j'ai 6 faces x 4 orientations = 24 façons de le poser.
Pour le premier cube, j'ai donc 9 possibilités de cubes x 24 façons pour chacun.
Pour le deuxième, 8 x 24; pour le troisième, 7 x 24 ..... et pour le dernier, 1 x 24.
Au final, pour la réponse A, je trouverais: 9! x (24^9) = env. 9,5856.(10^17), soit presque un milliard de milliards, soit presque 500 millions de fois plus que les deux milliards annoncés.
Mais je me suis probablement trompé quelque part: combien trouves-tu ?
Les questions suivantes me semblent par contre beaucoup plus ardues.
#7 - 21-01-2021 20:17:35
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Sudoku en couuleur
Question D :
Il faut choisir 4 couleurs parmi les 6, ce qui donne C(6,4) = C(6,2) = 15 cubes différents.
Question E :
Il faut commencer par choisir 9 cubes parmi les 15 possibles, soit C(15,9) = C(15,6) = 5005 possibilités.
Il reste à multiplier ce résultat par celui de la question A :
958659120196485120*5005 = 4798088896583408025600 (environ 0.480e-22).
#8 - 21-01-2021 22:59:47
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
#9 - 22-01-2021 16:13:31
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Sudoku e couleur
Voici quelques réponses partielles au fur et mesure de ma réflexion (pour ne pas
te faire croire à un lâche abandon:  ): ):
A) Merci d’avoir confirmé mon post précédent.
Résultat A = 9! x (24^9) = env. 9,5856.(10^17)
B) Ca se complique: affaire à suivre ….
C) Je trouve:
- nombre de permutations de lignes complètes de cubes = 3! = 6
- nombre de permutations de colonnes complètes de cubes = 3! = 6
- nombre de rotations du plateau complet = 4
Résultat C = 3! x 3! x 4 = 144
D) Il est intéressant de noter que les 6 faces présentent tous les arrangements
possibles des 4 couleurs (soit justement 3! = 6), arrangements dont on n’a donc
plus à se préoccuper.
Résultat D = 6! / (4! x 2!) = 15
E) On choisit d’abord 9 cubes parmi 15, puis on les ‘’arrange’’.
Nombre de choix = 15! / (9! x 6!) = 5005
Nombre d’arrangements (comme pour A) = 9! x (24^9)
Résultat E = (15! / 6!) x (24^9) = env. 2,64.(10^21)
F) On aura probablement:
Résultat F = 5005 x Résultat B (mais il reste à trouver le résultat de B)
Je reviendrai pour le résultat B (et F) plus tard, mais à l’occasion confirmes (ou
infirmes) mes résultats pour C, D et E.
Merci bonne fin de journée.
#10 - 22-01-2021 18:13:02
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
#11 - 23-01-2021 06:22:48
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Sudoku e couleur
Je retente une réponse après une nuit qui a peut-être porté conseil: 
B) Premier cube = 9 x 24 / Deuxième cube = 8 x 4 / Troisième cube= 7 x 4 /
Quatrième cube = 6 x 1 / Cubes suivants = 1
J’en fais le produit et j’obtiens un résultat de plus du double de la valeur annoncée.
Résultat B = 1 161 216
C) En retournant complètement le plateau, je peux multiplier ma solution précédente
par 2.
Résultat C = 288
E) Erreur d’application numérique
Résultat E = env. 4,798.(10^21)
F) Résultat F = 5005 x Résultat B
Résultat F = 5 811 886 080
#12 - 23-01-2021 10:24:42
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
#13 - 23-01-2021 12:14:10
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Suddoku en couleur
J'avoue que les dénombrements, arrangements et autres probabilités n'ont jamais été ma tasse de thé. 
Pour la partie C, j'ai bien pensé faire pivoter chaque cube du même multiple d'angles droits, mais je pense que ça rentre déjà dans ce qui décompté ailleurs: wait and see.
Merci en tous cas pour ce casse-tête. 
#14 - 23-01-2021 16:09:08
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
sudoku eb couleur
Franky a écrit:Pour la partie C, j'ai bien pensé faire pivoter...
Autour de quel(s) axe(s) ?
#15 - 23-01-2021 19:14:50
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Sudoku ne couleur
Ah oui, mince ! On est en 3D. Je dois donc pouvoir faire pivoter les cubes pour faire apparaître les faces cachées (tous en même temps et dans le même sens, sinon on n'est plus conforme), et ce en lignes et en colonnes.
Ainsi je dois pouvoir multiplier mon résultat précédent par 4 x 4 = 16. J'en suis donc à 4608, mais là, ça me semble beaucoup: à voir ....
#16 - 23-01-2021 21:25:05
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
sudiku en couleur
Franky a écrit:je dois pouvoir multiplier mon résultat précédent par xxx. J'en suis donc à xxx, mais là, ça me semble beaucoup: à voir ...
Là, tu m'as dépassé  ! Mais, comme tu le disais auparavant : ! Mais, comme tu le disais auparavant :
je pense [qu'une partie] rentre déjà dans ce qui est décompté ailleurs
Enfin, je le crois et peut-être que ça se discute  . .
Par ailleurs, j'ai réfléchi et je reviens sur mon approbation (post 12) à propos de la question F.
Je pense que les combinaisons de 9 cubes à partir des N possibles ne sont pas toutes valables pour obtenir un sudoku : on ne peut pas choisir plus (ni moins) de trois cubes contenant de blanc, de même que pour chacune des autres couleurs... 
#17 - 24-01-2021 09:40:39
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Sudoku en ccouleur
Il faut que j'achète ce jeu (actuellement en promo chez N&D, sans faire de pub) pour manipuler ces cubes et affiner nos chiffres.
Pour info, sur la toile, des tutos explicitant la solution permet aussi de bien comprendre "ce qu'il se passe".
#18 - 24-01-2021 12:28:36
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Sudoku en coulur
Un cube est un arrangement de 4 couleurs sans repetition, il y 4! = 24 possibilités.
Avec 6 faces et 4 rotations, un cube de quatre couleurs données offre toutes les possibilités.
D = combinaison de 4 couleurs parmi 6 = 15 cubes
nous avons WBJO, WBJV, WBRO, WBRV, WJOR, WJRV, BJOV, JORV et BORV.
il nous manque WBJR, WBOV, WJOV, WORV, BJOR, BJRV disponible prochainement en extension de jeu.
E: 15!24^9/6!
A = arrangement de 9 cubes sans repetition
9!x24^9
9 choix pour le premier cube avec 24 possibilités
puis 8 choix et toujours 24 possibilités, etc
cela nous donne moins d’1 solution par million d'arrangements (en supposant 500 000 solutions)
B =
on s'affranchi de la restriction des cubes et on simplement arrange 6x6 couleurs suivant les regles de Sudoku.
6x5x4x3x2x1 pour la premiere ligne
5x4x3x2x1x1 pour la seconde...
4x3x2x1x1x1 ...
...
soit 6!x5!x4!x3!x2!= 25 millions de solutions
les cubes ont des couleurs differentes ce qui reduit le nombre de possibilités...
---
le premier cube 9*24 possibilités; disons WB/JO
le second cube doit contenir 2 colours différentes du premier cube pour avoir une solution, il y a toujours 4 cubes possibles.
WB/JO+RV/WB(4 pemutations) ou JR/WV(2x4) ou JO/RV(4) ou OR/BV(2x4)
soit 24 possibilités
le troisieme cube de cette ligne a ces couleurs imposées avec 4 permutations.
donc 9*24*28*4=12096 pour cette premiere ligne
je passe la main pour la suite:P
The proof of the pudding is in the eating.
#19 - 24-01-2021 18:11:21
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
#20 - 25-01-2021 09:10:32
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Suudoku en couleur
Une méthode de résolution consiste à disposer les cubes sur le plateau, sans se préoccuper, dans un premier temps, de leur orientation, en faisant en sorte que chaque double colonne (largeur du cube) et chaque double ligne (hauteur du cube) contiennent deux fois chacune des six couleurs (même alignées). Dans le cas contraire, il faut intervertir deux cubes jusqu’à obtention de cet objectif. Puis, dans un second temps, on oriente chacun des cubes, sans le déplacer vers une autre position, pour avoir une couleur unique par ligne et par colonne.
Avec cette méthode, on doit pouvoir affiner nos chiffres. J'y retournerai dès qu'un peu de temps se libèrera (milieu de cette semaine).
Bonne journée.
#21 - 25-01-2021 10:36:36
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
#22 - 29-01-2021 22:41:29
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
sudoku zn couleur
Avec un peu de retard, je remercie tous ceux qui se sont intéressé à mon questionnement  , et qui y ont apporté des réponses, même partielles. , et qui y ont apporté des réponses, même partielles.
En résumé :
A) Pourrait-on avoir une idée plus précise du nombre total d'arrangements ?
9 choix possibles pour choisir un premier cube, 8 pour le second, ... En tout 9! possibilités de placer ces cubes sur le plateau.
Pour chaque cube 6 faces orientables dans 4 directions soit 24**9 possibilités.
Au total : 9! * 24**9 = 958 659 120 196 485 120 arrangements, soit près de un milliard de milliard de possibilités !
B) Quel est le nombre exact de solutions compatibles avec les règles du Sudoku ?
N'étant pas très sûr de mon résultat  , et celui-ci n'étant pas tout à fait conforme avec celui inscrit sur la boîte , et celui-ci n'étant pas tout à fait conforme avec celui inscrit sur la boîte  , je préfère ne pas l'exposer de suite, en espérant qu'un véritable matheux vienne présenter son point de vue. , je préfère ne pas l'exposer de suite, en espérant qu'un véritable matheux vienne présenter son point de vue.
C : Combien de solutions peut-on obtenir facilement à partir d'une solution de Sudoku valable ?
- par rotation d'axe verticale du plateau, 4,
- par permutation de lignes et de colonnes, 6x6 = 36.
- par retournement du plateau, 2
Contrairement à ce que j'ai pu penser au départ, les rotations colonnes par colonnes ou lignes par ligne ne donnent pas de solutions valables , pas plus que les rotations de chaque cube autour d'un axe vertical (j'avoue que c'est plus facile de s'en rendre compte quand on a le jeu entre les mains !).
Au total 4 x 36 x 2 = 288 variantes.
D) Combien de cubes différents N peut-on fabriquer à partir de ces six couleurs ?
Il s'agit des combinaisons de 4 couleurs parmi 6.
On peut donc obtenir 15 cubes différents.
E) A partir de ces N cubes, combien d'arrangements existe-t-il pour remplir la boîte de 9 cubes ?
Il faut commencer par choisir 9 cubes parmi les 15 possibles, soit C(15,9) = 5005 possibilités.
Il reste à multiplier ce résultat par celui de la question A, soit :
4 798 088 896 583 408 025 600 possibilités.
F) Parmi ces arrangements, combien de solutions respectent la règle du Sudoku ?
Il faut commencer par choisir 9 cubes parmi les 15, mais toutes les combinaisons ne sont pas possibles : il faut en plus que chaque couleur apparaisse 6 fois, ni plus, ni moins. Il y a donc 3 cubes qui ne possèdent pas de blanc, 3 pas de bleu, etc...
Pour la première couleur manquante, il faut choisir 3 autres couleurs parmi 5, soit 10 combinaisons.
Pour la seconde, il ne faut plus en choisir que 2 parmi 4, soit 6 combinaisons.
Pour la troisième, 2 parmi 3, soit 3 combinaisons.
Pour la quatrième et la suite, il n'y a plus qu'une seule possibilité.
Nous avons donc en tout 10*6*3 = 180 combinaisons de neuf cubes.
Il ne reste plus qu'à multiplier ce résultat par celui que l'on aura trouvé à la question B  ! !
Maintenant, j'ai toujours eu des difficultés avec les maths, et il m'arrive fréquemment de faire des bourdes  ! Je me tiens donc prêt à accueillir toutes les suggestions et les contradictions que vous voudrez bien me signaler ! Je me tiens donc prêt à accueillir toutes les suggestions et les contradictions que vous voudrez bien me signaler  . .
#23 - 03-02-2021 14:51:58
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Sudku en couleur
B) En dénombrant les arrangements compatibles avec les règles du sodoku, je trouve un nombre compris entre 2000000 et 3000000. De plus ce nombre est divisible par 289.
#24 - 03-02-2021 16:35:32
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
sydoku en couleur
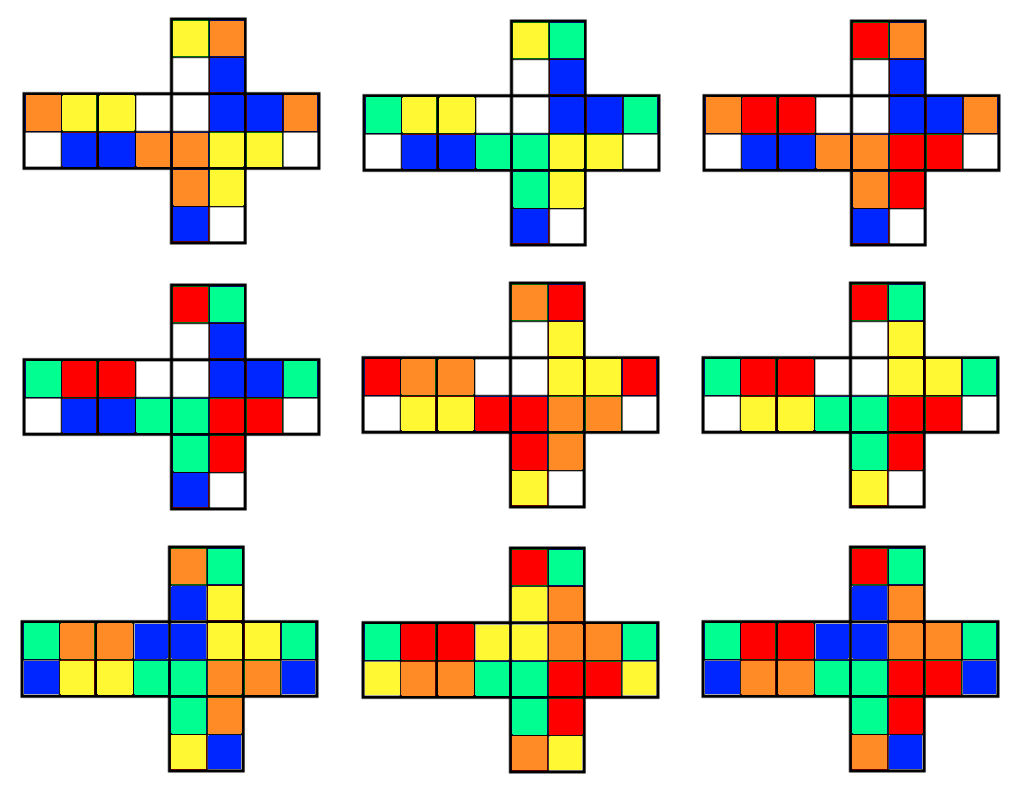
Sans vouloir faire concurrence aux marchands du jeu, voici les patrons pour construire ces neuf cubes et les manipuler pour mieux comprendre ce qui se passe. N'oubliez pas les onglets d'assemblage non dessinés ici.
#25 - 04-02-2021 15:48:40
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum