Bon, ma méthode ne prouve rien mais j'ai testé "betement" tous les cas :
à partir des 42 partitions du chiffre 10 :

10
9+1
8+2
8+1+1
7+3
7+2+1
7+1+1+1
6+4
6+3+1
6+2+2
6+2+1+1
6+1+1+1+1
5+5
5+4+1
5+3+2
5+3+1+1
5+2+2+1
5+2+1+1+1
5+1+1+1+1+1
4+4+2
4+4+1+1
4+3+3
4+3+2+1
4+3+1+1+1
4+2+2+2
4+2+2+1+1
4+2+1+1+1+1
4+1+1+1+1+1+1
3+3+3+1
3+3+2+2
3+3+2+1+1
3+3+1+1+1+1
3+2+2+2+1
3+2+2+1+1+1
3+2+1+1+1+1+1
3+1+1+1+1+1+1+1
2+2+2+2+2
2+2+2+2+1+1
2+2+2+1+1+1+1
2+2+1+1+1+1+1+1
2+1+1+1+1+1+1+1+1
1+1+1+1+1+1+1+1+1+1

J'ai généré pour chacune toutes les permutations possibles. (512 en tout)

Et j'ai lancé une fonction de calcul (en PHP, je n'avais que ça sous la main) :

function escalier($tasdepieces) {
 $pos_actuelle = $tasdepieces;
 $pos_precedente = array();
 while ($pos_actuelle != $pos_precedente) {
  $pos_precedente = $pos_actuelle;
  $nb_tas = count($pos_actuelle);
  for ($i = 0; $i < $nb_tas; $i++) {
   $pos_actuelle[$i]--; // on enleve une pièce
   if ($pos_actuelle[$i] == 0) unset($pos_actuelle[$i]); // on enleve un tas
  }
  $pos_actuelle[] = $nb_tas; // rajoute le tas
  $pos_actuelle = array_values($pos_actuelle); // evite les problème de clef
 }
 return $pos_actuelle;
}

Aucune position de départ ne donne autre chose que 1 2 3 4.

J'en ai profité pour calculer le nombre d'étapes, en posant systématiquement la nouvelle pile à droite des premières.

Les cas les plus défavorables sont :
3 3 2 1 1, 3 2 2 2 1 et 3 2 2 1 1 1 avec 16 mouvements.

c'est l'unique position invariante, reste a voire pourquoi toutes situations y arrivent

j'edite des que j'ai des idées

EDIT1:
a ben, je viens de tomber sur un contre exemple
655322
6544211
754331
664322
6553211
754421
664331
655322

et en l'étudiant un peu c'est logique, lorsque 2 valeurs sont égales, on se retrouve avec un "trou" ailleurs dans l'escalier, et donc a un moment on va avoir 1 étape sans avoir de 1, et donc on va se retrouver avec 2 chiffres crées identiques, et donc on perpétue l'erreur initial.

par contre avec une sommes de 10, il est impossible de crée une liste avec 2 valeurs égales et un trou.. je pense donc qu'a 10 toutes situation arrive a l'equilibre

EDIT2:
ca semble pas suffisant, j'ai pu trop de temps, je regarderai ca plus tard !

La réponse est "oui" pour 10 pièces.

Je pense l'avoir vérifié sur excel en balayant toutes les combinaisons.
Par contre, je n'ai pas de démo complète... mais des bribes d'idées :

1. Si il existe une position invariante par l'opération, celle-ci ne peut être que 4 3 2 1.
En effet : la position invariante contient une unique pile de 1 (pour conserver le nombre de pile). Toutes les autres piles vont être diminuées de 1, donc la pile la plus haute doit être engendrée par la nouvelle pile créée et toutes les valeurs entre 1 et cette hauteur doivent être présentes.
Donc, les piles invariantes sont du type 1 2 .... n.

rem : si on démarre avec un nombre de pièces différent de P(1)=1 P(2)=3 P(3)=6 P(4)=10 P(5)=15 etc, il n'y a pas de position invariante, mais des périodes de tailles n+1 pour un nombre de pièces initiales compris entre P(n) et P(n+1).

2. J'ai ensuite essayé de trouver une mesure de l'écart par rapport à la position invariante et de montrer sa décroissance stricte...
Je n'ai rien trouvé : si on prend, par exemple, la somme des écarts (en valeur absolue) de la position actuelle ordonnée par rapport à la position invariante, on observe que ça décroit mais pas de façon stricte, donc ça ne prouve rien.

Donc je sèche...

Si on part de 3 3 2 1 1, il faut 12 opérations pour arriver à 4 3 2 1, alors que visuellement, c'est proche de 4 3 2 1 (plus proche que 6 4 qui ne demande que 2 opérations).
Tous les chemins passent par 5 3 2.

J'attends avec impatience les indices ou la solution pour m'extasier sur le beau modèle mathématique qu'il convient de coller sur ce problème.

Merci pour l’indice qui éclaire tout !

On suppose que l’on démarre avec les piles (ou colonnes) ordonnées de la plus grande en X=0 vers la plus petite et on note la hauteur de chaque pièce par son ordonnée Y (Y=0 pour la pièce du bas).


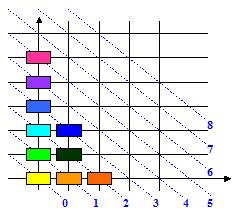
exemple : Position 1 :

En prenant les pièces en bas de la pile, il est clair qu'une opération de distribution conserve les pièces sur une même ligne de niveau. J’appelle ligne de niveau n une ligne pour laquelle X + Y = n.

En effet, une distribution revient à faire : si Yi=0, Yf=Xi et Xf=Yi et sinon, Yf=Yi-1 et Xf=Xi+1.

Distribution : passage de pos1 à pos2


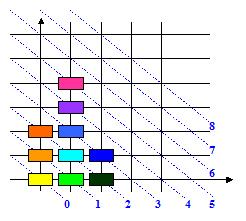
Position 2 :

Donc, si on prend comme mesure du désordre E d’une position la somme des niveaux de chaque pièce, ce désordre E est invariant par distribution.


Si la colonne créée (ou n’importe quelle autre colonne d'ailleurs) possède moins de pièces que celle sur sa droite, il convient de trier les colonnes. Ce tri revient à déplacer sur la gauche les pièces n’ayant pas de voisins à gauche.

Tri : passage de pos2 à pos3.


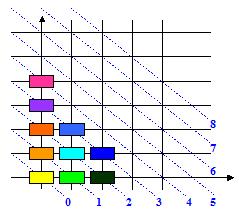
Position 3 :

Le tri diminue le désordre (puisqu’au moins une pièces passe à Xf=Xi-1).


Démontrons maintenant que l’on obtient toujours la position 4 3 2 1, qui correspond au désordre minimal E=20 :

Si l’on n’est pas sur la position 4 3 2 1, il existe donc une colonne pour laquelle la pièce supérieure n’est pas sur le niveau 3, et il existe aussi une colonne pour laquelle il y a une pièce sur le niveau 4.

Par distributions successives, le trou du niveau 3 et la pièce du niveau 4 se déplacent vers la droite sur leur ligne de niveau respective.

Le trou se déplaçant sur le niveau 3 va prendre successivement 4 positions, la pièce se déplaçant sur le niveau 4 va prendre successivement 5 positions. Donc, 4 et 5 étant premiers entre eux, au bout de 20 distributions maxi, on aura le trou niveau 3 sur une colonne et la pièce niveau 4 sur la colonne juste à droite, on pourra donc faire un tri et diminuer le désordre E.

Cette opération réduit de 1 au moins le désordre et peut être répétée tant que l'on ne se trouve pas sur la position 4 3 2 1, donc on atteindra E=20 (donc la position 4 3 2 1).

Cqfd.


Rem : la démonstration s’applique pour n’importe quel nombre de pièces initiales. Si le nombre de pièces permet d’avoir une position où tous les niveaux sont pleins (1 3 6 10 15 21 etc), cette position invariante est la position finale. Sinon, on obtient une suite périodique de positions (de désordre le plus faible possible), les positions de la périodes correspondant au déplacement des pièces sur le niveau incomplet (par distribution mais sans tri) : d’où la période égale au nombre de positions du niveau incomplet.

Encore un beau problème de Vasimolo ! Bravo !