 |
#1 - 28-06-2010 22:32:08
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
Blaade sur un carré
Ceci est une question assez facile, accessible à tous ; toutefois, les prépas et plus auront un avantage car ils ont plus d'outils pour résoudre le problème. Je prépare la suivante qui lui est semblable en montant en dimension. (Je ne l'ai pas trouvée dans le forum)
je me déplace uniquement sur les côtés d'un carré*. Combien de balades différentes commençant par [latex]A[/latex] et finissant par [latex]B[/latex], et de exactement [latex]n[/latex] déplacements, existe-t-il dans les cas suivants ?
[* ie 1 déplacement se fait d'un sommet à un sommet adjacent = pas de diagonale autorisée]
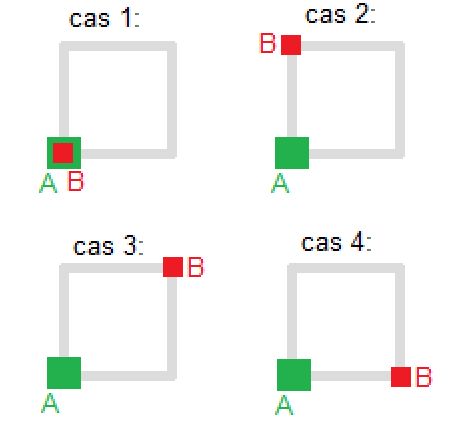
Exemple de solution particulière, cas 1 avec n=2, on peut soit monter puis redescendre, soit aller droite et revenir à gauche, donc il y a 2 balades possibles.
Vous devez donner une solution générale, fonction de [latex]n[/latex].
Spoiler : Indice pour ceux qui sont bloqués Il y a plusieurs façons de répondre, dont une utilisant le dénombrement, et une la récurrence.
#2 - 29-06-2010 00:47:14
- Bamby2
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 152
valade sur un carré
il faut dans un premier temps "aller au coin opposé" puis a partir de la, pour chaque '2 pas' on a deux choix, on part d'un coté (et on revient) ou bien l'on part de l'autre.
cas 1:
la longueur est pair, si n est impair, il n'existe pas de chemin.
sinon pour n=2k il existe 2*2^(k-1)=2^k chemins.
cas 2 et 4 qui sont identique:
la longueur est impair, si n est pair, il n'existe pas de chemin.
si n=1 il existe 1 chemin,
si n=2k+1 il existe 2^k chemins.
cas 3:
la longueur est pair, si n est impair, il n'existe pas de chemin.
sinon pour n=2k, il existe 2^k chemins.
edit: j'ai concidéré qu'on ne pouvais pas revenir a l'origine, mais je me rends compte que j'ai peut etre tort ?
#3 - 29-06-2010 15:54:11
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Balade sur un carér
Cas 1: 0 si N est impair ou inférieur à 2, 2^(N-1) sinon
En effet, on constate qu'en 2 mouvements, on peut soit revenir au point de départ, soit aller à son opposé. Du coup, pour un nombre impair de mouvement on se retrouve toujours sur un coin adjacent au point de départ, et pour un nombre pair, on a à chaque fois 2 chemins possibles (continuer dans le même sens ou rebrousser chemin), sauf pour la dernière étape où il est nécessaire de revenir au point de départ.
Cas 3: pareil (sauf qu'on doit finir sur le coin opposé et pas le point de départ)
Cas 2:
Soit on part directement sur le point d'arrivée, et dans ce cas, on se ramène au cas 1, soit on part directement sur le point opposé et on se ramène au cas 3.
On a donc 0 si N est pair, et 2^(N-1) si N est impair
Cas 4: idem que le cas 2 (par symétrie)
#4 - 29-06-2010 16:55:59
- Nicouj
- Professionnel de Prise2Tete
- Enigmes résolues : 27
- Messages : 330
Baladee sur un carré
Quand je me ballade entre 2 sommets en me déplaçant sur n cotés, je passe par n+1 sommets dont le seul le premier et le dernier sont fixés.
La séquence des autres sommets est une alternance entre les sommets de chaque diagonale.
Donc pour les n-1 sommets non fixés j'ai 2 possibilités à chaque fois.
De plus les ballades d'un sommet vers un sommet d'une même diagonale auront forcément un nombre pair d'étapes/ Et vers un sommet d'une autre diagonale, un nombre impair d'étapes.
D'un sommet vers lui même en 2n étapes nous aurons [latex]1[/latex] chemin si n=0 (on bouge pas) et [latex]2^{2n-1}[/latex] sinon car le chemin aura (2n-1) sommets de transition avec 2 possibilités chaque fois.
D'un sommet vers l'autre sommet de la diagonale idem sauf pas de ballade "nulle" possible
D'un sommet vers un sommet adjacent (appartenant à une autre diagonale) en 2n+1 étapes nous aurons [latex]2^{2n}[/latex] chemins car il y aura 2n sommets de transition avec 2 possibilités chaque fois.
#5 - 29-06-2010 17:13:23
- scrablor
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 965
Balade sur un caré
Le nombre de parcours est invariablement 2^n pour tout n.
Si n est impair : on ne peux réaliser que le cas 2 ou le cas 4, à égalité vu la symétrie, donc 2^(n-1) pour chacun et zéro pour les deux autres.
Si n est pair non nul : on ne peux réaliser que le cas 1 ou le cas 3, à égalité de chances également, on le voit dès le premier déplacement. C'est encore 2^(n-1) pour ceux-là et zéro pour les cas 2 et 4.
Si n est nul : Une seule possibilité... qui nous laisse au départ !
Voilà pour les balades. Quant aux ballades, je ne sais pas... ça dépend de ce que tu as dans ton baladeur.
Celui qui fuit les casse-tête ne vaut pas un clou.
#6 - 30-06-2010 00:45:46
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
balade sur un varré
bravo à scarta, nicouj et scrabblor; attelez vous-y c'est pas très difficile avec un peu d'astuce...
#7 - 30-06-2010 04:34:26
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
BBalade sur un carré
en supposant que l'on ne repasse pas plusieurs fois au meme endroit je dirais 2 solutions pour chaque cas:
1) 4 & 4
2) 1 &3
3) 2 & 2
4) 3 & 1 mouvements.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#8 - 30-06-2010 13:02:39
- clementmarmet
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 1329
- Lieu: I'm in spaaaace!!
Balade sur un arré
les points étant sur un 'circuit', il n'y a chaque fois que 2 trajets, dans un sens et dans l'autre 
eki eki eki pa tang!!
#9 - 30-06-2010 13:57:54
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
Ballade sur un carré
dhrm, tu peux repasser partout, puisque n peut etre tres grand.
clementmarnet, tu peux développer et donner une solution ?
#10 - 30-06-2010 15:01:17
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
bamade sur un carré
Trop d'énigmes ces temps-ci, pas le temps d'assez réfléchir, argh...
Essayons en blitz mode 
Cas 1 et cas 3:
Ces 2 cas me semblent tout à fait semblables.
n doit être pair sinon impossible de revenir au départ.
Seul le dernier déplacement est imposé pour revenir au départ, les n-1 déplacements précédents sont libres et il y a 2 possibilités pour chacun d'entre eux. Par ailleurs, construite sur le choix à chaque mouvement, elles sont toutes différentes (il n'y à qu'à les coder en binaire pour s'en convaincre).
Il y a donc [latex]2^{n-1}[/latex] balades pour n pair pour ces 2 cas et 0 si n impair
Cas 2 et cas 4:
Ces 2 cas me semblent eux aussi tout à fait semblables.
n doit être impair cette fois, sinon impossible de revenir au départ.
Le même raisonnement me semble correct: seul le dernier déplacement est imposé pour revenir au départ, les n-1 déplacements précédents sont libres et il y a 2 possibilités pour chacun d'entre eux.
Il y a donc aussi [latex]2^{n-1}[/latex] balades pour n impair pour ces 2 cas et 0 si n pair
Bon, j'espère ne pas être grossièrement passé à côté du problème, un énorme hors-sujet en cette période d'examens 
Mais en tout cas, cette énigme était assez différente de ce que l'on voit d'habitude. Merci.
#11 - 30-06-2010 15:03:22
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
#12 - 30-06-2010 15:07:07
- emmaenne
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3073
- Lieu: Au sud du Nord
Blade sur un carré
Moi j'attends de voir les réponses ici pour essayer le cube. 
Dans le cadre de la quinzaine du beau langage, ne disez pas disez, disez dites. (Julos Beaucarne)
#13 - 30-06-2010 15:16:45
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
balafe sur un carré
haha, je doute que les réponse ici t'aident pour le cube, tant les approches pour le cube sont plus compliquées... Tu devrais y réfléchir un peu à ce carré, je me fais aucun soucis, la réponse n'est pas très loin.
#14 - 01-07-2010 01:37:57
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
Balade sur unn carré
voilà donc ma réponse, sous plusieurs formes. Les deux premières sous spoiler peuvent être étendues au cube, mais ce n'est pas évident. La troisième me semble simple, astucieuse et convaincante, c'est celle qu'il faut retenir dans ce cas.
Spoiler : dénombrement ---------- Solution 1 : Dénombrement ------------------
Pour cette démonstration, je ne vais faire qu'un seul cas, disons le cas 2, parce que ce n'est pas la solution la plus élégante et qu'il faut s'accrocher (un peu) pour les formules. En revanche, c'est une solution "facile" à étendre aux dimensions supérieures.
On modifie le problème : au lieu de se déplacer sur le carré, on se déplace sur une grille (en partant du coin en bas à gauche), toujours vers le haut ou vers la droite. A ce moment, ce sont les parités de l'ordonnée et de l'abscisse d'arrivée qui caractérisent les différents cas :
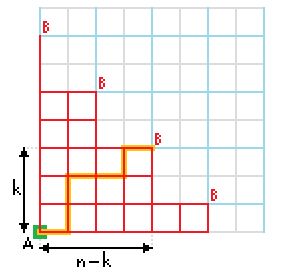
Ici, dans le cas 2, il faut se déplacer verticalement un nombre impair de fois, et horizontalement un nombre pair de fois (lignes bleu ciel sur la grille), et il faut bien entendu que [latex]n[/latex] soit impair (dans l'exemple, on prendra n=7).
Les ballades possibles empruntent donc les lignes rouges du dessin (un exemple de ballade est donnée surligné en orange), et arriveront jusqu'aux différents [latex]B[/latex] possibles.
Maintenant, un [latex]B[/latex] de la grille étant choisi, (dans l'exemple on choisit celui qui est à l'arrivée de la ligne orange) combien y a-t-il de manières d'y arriver ? Et bien il s'agit de choisir quand on monte (il faut monter [latex]k[/latex] fois parmi les [latex]n[/latex] déplacements possibles.
Donc pour aller à ce [latex]B[/latex] de la grille, il y a :
[TeX]C^k_n[/latex] balades ([latex]C^3_7= \frac{7!}{(7-3)! 3!}=35[/latex] balades dans l'exemple)
et ceci est valable pour tous les [latex]k[/latex] tels que [latex]0 \leq k \leq n[/latex], avec [latex]k[/latex] impair (parce qu'on est dans le cas 2).
Donc le résultat final est :
[latex]S_{2}(n)=\sum_{0 \leq 2i+1 \leq n} C^{2i+1}_{n}[/TeX]
C'est la somme des termes impairs.
Or, en notant [latex]S_{3}(n)=\sum_{0 \leq 2i \leq n} C^{2i}_{n}[/latex] la somme des termes pairs, on a :
[TeX]S_{2}(n)+S_{3}(n)= \sum_{k=0}^{n} C^{k}_{n}= \sum_{k=0}^{n} C^{k}_{n} 1^{k} 1^{n-k}={(1+1)}^{n}=2^{n}[/TeX]
Or [latex]S_{3}(n)[/latex] correspond au cas 3 (avec [latex]n[/latex] toujours impair je le rappelle), qui est symmétrique du cas 2... donc ces sommes sont égales, et le résultat est que la solution est dans ces cas :
[TeX]S_2(n)=S_3(n)=2^{n-1}[/latex]
Spoiler : récurrence ---------- Solution 2 : Récurrence ------------------
Ici, on va utiliser la récurrence. En remarquant qu'après un déplacement, tous les cas sont identiques, on note [latex]u(n)[/latex] la solution. En effet, les cas 2 et 3 sont évidemment semblables, et les cas 1 et 4 sont identiques après le premier déplacement. La parité déterminant de quel cas on parle.
On a donc la récurrence directement :
[latex]\left{ \begin{array}{l} u(0)=1 \\ u(1) = 1 \\ u(n+1)=2u(n) \end{array}\right.[/TeX]
soit [latex]u(n) = 2^{n-1}[/latex]
Avec la convention donc que [latex]u(0)=1[/latex] tient pour le cas 1 uniquement, [latex]u(2k)[/latex] pour les cas 1 et 4, et [latex]u(2k+1)[/latex] pour les cas 2 et 3.
---------- Solution 3 : élégance ------------------
Remarquant que les cas 2 et 3 sont symmétriques, et que les cas 1 et 4 le sont aussi après 1 déplacements, il vient de suite qu'en tenant compte de la parité, chaque solution est de la forme [toutes les ballades possibles] / 2, d'où, directement :
[TeX]S(n) = 2^{n-1}[/TeX]
Ne vous emballez pas, ce genre d'analyse ne fonctionne pas pour le cube !
#15 - 01-07-2010 18:02:04
- emmaenne
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3073
- Lieu: Au sud du Nord
Ballade sur un carré
haha, je doute que les réponse ici t'aident pour le cube, tant les approches pour le cube sont plus compliquées... Tu devrais y réfléchir un peu à ce carré, je me fais aucun soucis, la réponse n'est pas très loin.
et bien si, j'ai eu raison d'attendre. Je sais que je trouverai pas pour le cube étant donné que je n'ai rien compris aux solutions 
Dans le cadre de la quinzaine du beau langage, ne disez pas disez, disez dites. (Julos Beaucarne)
#16 - 01-07-2010 20:40:20
- clementmarmet
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 1329
- Lieu: I'm in spaaaace!!
Balade sur un acrré
désolé je n'avais pas compris qu'il fallait 'compter' les déplacements 

eki eki eki pa tang!!
#17 - 02-07-2010 18:24:44
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
Baade sur un carré
emmaenne a écrit:haha, je doute que les réponse ici t'aident pour le cube, tant les approches pour le cube sont plus compliquées... Tu devrais y réfléchir un peu à ce carré, je me fais aucun soucis, la réponse n'est pas très loin.
et bien si, j'ai eu raison d'attendre. Je sais que je trouverai pas pour le cube étant donné que je n'ai rien compris aux solutions 
Alors je te refais la démo élégante pas à pas...
Tout d'abord, on part du point de départ :
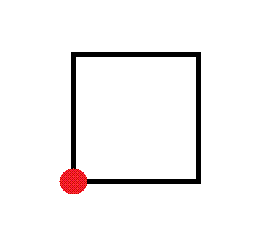
Ensuite, on peut se déplacer vers la droite ou vers le haut :
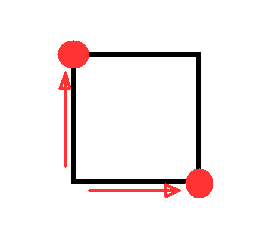
A partir de là, la situation est clairement symmétrique entre être sur un point bleu ou un point vert, comme part exemple après 2 déplacements (les 4 deuxièmes déplacements possibles sont les flèches bleues) :
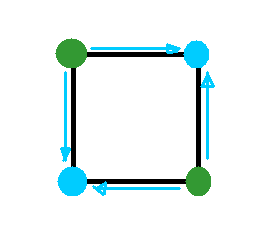
Donc comme on a la parité de [latex]n[/latex] qui détermine si l'on est sur un point bleu ou vert, et qu'avec [latex]n[/latex] déplacements, il y a [latex]2^n[/latex] balades possibles (il y a toujours le choix entre deux déplacements à chaque fois), c'est que le nombre de balades possibles pour être en un point spécifique est :
- 0 si la parité ne le permet pas (ie vert et pair, ou bleu et impair),
- [latex]\frac{2^n}{2}=2^{n-1}[/latex] si la parité le permet (On divise par 2 parce qu'on est sur 1 seul des 2 points bleus, ou sur 1 seul des 2points verts !).
Convaincue ?
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum









