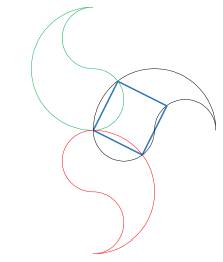|
#1 - 16-12-2014 19:55:39
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Le arré caché
salut à tous.
la figure ci dessous est composée de 3 demi cercles , un de rayon 100 mm et 2 de rayon 50 mm .
j'ai tracé un carré dont les 4 sommets appartiennent à l'un ou à l'autre de ces trois demi-cercles.
question: quelle est la superficie de ce carré ?
bon courage.

#2 - 16-12-2014 20:57:32
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
Le carréé caché
Sauf erreur (ça me semble trop trivial pour le genre d'énigme que tu poses) :
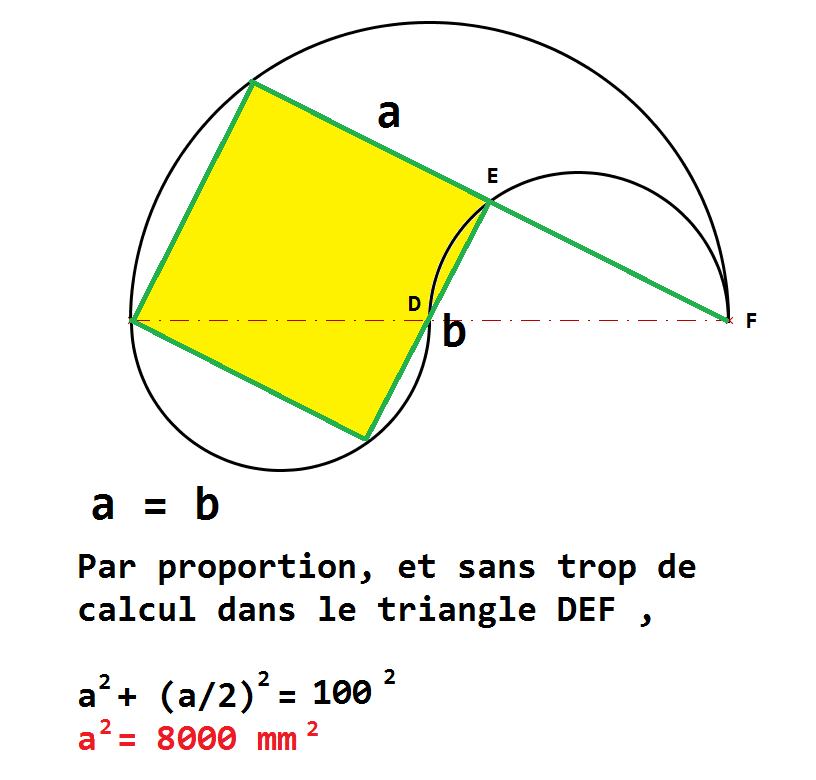
Edit : je viens de me rendre compte que j'ai confondu rayon et diametre...
Ca donne donc 8000 , pas 2000
#3 - 16-12-2014 21:50:55
- Sydre
- Professionnel de Prise2Tete
- Enigmes résolues : 15
- Messages : 245
Le carré cach
Environ 20cm² 
#4 - 16-12-2014 21:59:53
- cogito
- Expert de Prise2Tete
- Enigmes résolues : 48
- Messages : 593
me carré caché
Bonjour,
Dans l'image ci dessous :
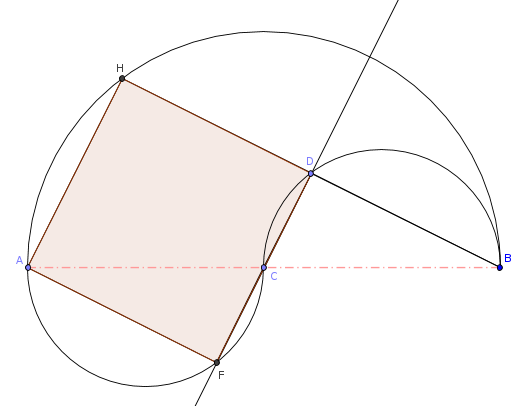
Nous avons :
CD = CF et donc FD=2CF
Comme AFDH est un carré alors AF = FD = 2CF
De ceci on peut également déduire que l'aire du carré est :
AF² = (2CF)² = 4CF².
De plus le triangle ACF étant rectangle en F donc nous avons :
CF²+AF²=AC² soit CF²+(2CF)² = 100²
autrement dit 5CF²=10000 soit CF²=2000 soit 4CF²=8000
l'aire du carré est donc 8000 mm² soit 80 cm²
Il y a sûrement plus simple.
#5 - 16-12-2014 22:17:45
- kikikiki
- Amateur de Prise2Tete
- Enigmes résolues : 2
- Messages : 2
#6 - 16-12-2014 22:20:40
- kikikiki
- Amateur de Prise2Tete
- Enigmes résolues : 2
- Messages : 2
#7 - 17-12-2014 00:18:12
- enigmatus
- Expert de Prise2Tete
- Enigmes résolues : 0
- Messages : 561
Le carré cché
Bonsoir,
1) 0 (4 points confondus).
2) 80 cm2 : 2 points (1 sur chacun des petits cercles) symétriques par rapport au centre du grand cercle, 1 point commun au grand cercle et au petit cercle de gauche, le 4ème sur le grand cercle complète le carré.
#8 - 17-12-2014 08:58:56
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
me carré caché
salut.
@cogito & énigmatus: bien vu !
@ gwen27 pas si trivial que ça finalement. non !
@ sydre : non , calcule la surface totale et tu verras .
@ kikikiki : une aire ne s'exprime ni en m ni en mm
#9 - 17-12-2014 09:07:28
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
ke carré caché
 J'ai beau chercher, j'ai bien 3 angles droits, donc 4. et 2 côtés adjacents de même longueur. Je ne trouve pas l'erreur, je retombe sur 8000 mm^2. J'ai beau chercher, j'ai bien 3 angles droits, donc 4. et 2 côtés adjacents de même longueur. Je ne trouve pas l'erreur, je retombe sur 8000 mm^2.
Il n'est pas là où je l'ai mis ton carré ?
Ou alors c'est parce que tu n'as pas lu l'édit en bas de message alors que j'ai négligé de changer l'image dans le même temps. "F5" devrait donner la bonne image maintenant.
#10 - 17-12-2014 09:40:19
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Le carré cach
Deux points du carré seront forcément sur le grand demi-cercle et chacun des deux autres points sur chacun des deux petits demi-cercles.
La perpendiculaire à la droite reliant les deux points du grand demi-cercle passant par leur milieu passera par l’origine d’un repère centré sur le milieu de la figure. Donc les deux points des petits demi-cercles seront symétriques par rapport à l’origine.
Dans ce repère, le demi-cercle en bas à droite a pour équation: (x-50)² + y² = 2500
Soit x0 l’abscisse du point du carré en bas à droite. On aura: y0 = V[2500-(x0-50)²]
Le côté du carré vaut: c = 2.V(x0²+y0²) = 2.V(100.x0) = 20.V(x0)
J’écris Pythagore pour que cette valeur du côté soit aussi celle des trois autres côtés:
[10.V(x0)]² + [20.V(x0)]² = 10000 => x0 = 20
Le côté du carré vaut donc: c = 40.V(5), et sa superficie: s = c² = 8000 mm²
#11 - 17-12-2014 09:46:09
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 381
Le caré caché
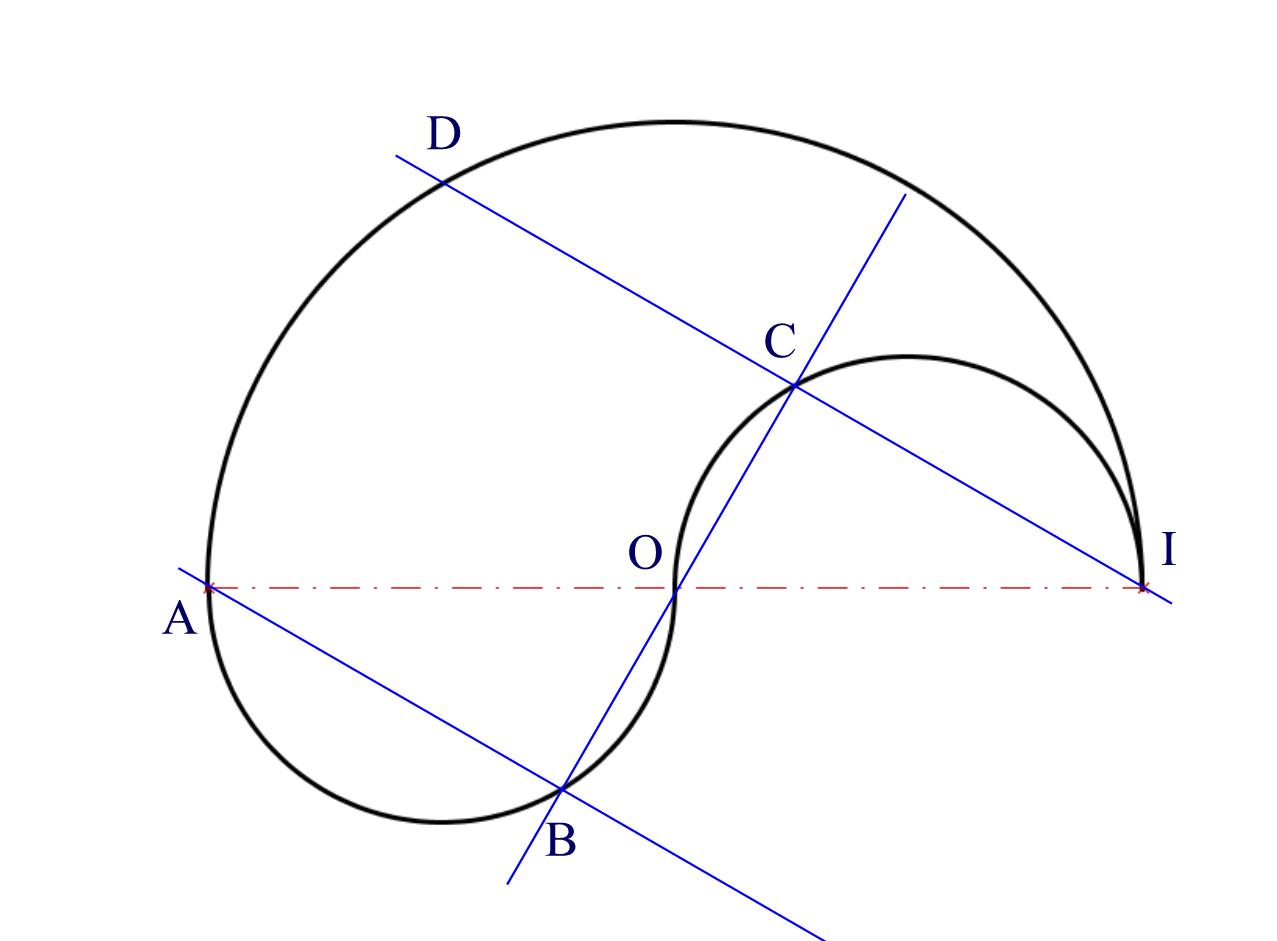
On nomme A, O et I sur le diamètre du grand cercle.
On trace une droite passant par O et coupant les 2 petits demi-cercles en B et C.
On trace ensuite la droite (IC) qui coupe le grand cercle en D.
Les triangles ABO, OCI sont rectangles (hypoténuse est un diamètre).
[DA] est l'image de [CO] par une homothétie de centre I, donc (DA) est parallèle à (CO).
Donc ABCD est un rectangle.
En choisissant B tel que AB=2OB, ABCD est un carré, de coté a qui vérifie a²+(a/2)²=AO², donc a²=4/5 AO²=8000 mm²
J'ai la très forte impression que c'est l'unique placement possible d'un carré sur la figure, mais je n'ai pas la démonstration.
#12 - 17-12-2014 10:54:47
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Le carré aché
@dylasse & francky bien vu.
@ gwen . ok maintenant , tu avais mis ton résultat en rouge et ton édit était beaucoup plus bas , je ne l'ai pas vu , autant pour moi .
nb. j'ai consulté les réponses avant ta modif et je n'ai répondu que ce matin .
#13 - 17-12-2014 12:11:03
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
lr carré caché
Il parait qu'il est toujours possible de trouver quatre points formant un carré sur une courbe fermée tracée dans un plan et ne passant pas deux fois par le même point, sans même que cette courbe soit dépourvue de cassures (points d'inflexion).
http://images.math.cnrs.fr/Un-carre-dan … ourbe.html
#14 - 17-12-2014 16:45:48
- NickBern
- Passionné de Prise2Tete
- Enigmes résolues : 45
- Messages : 50
LLe carré caché
Le carré a pour côté 8,9442 mm environ, soit une aire de 0,007999871364 m²
 ? ?
#15 - 17-12-2014 17:37:16
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
e carré caché
Sans preuve, j'ai trouvé avec un peu de chance en faisant tourner la figure de 90° et -90° autour de son point le plus à gauche.
#16 - 17-12-2014 17:47:15
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Le caarré caché
Bonjour unencoudee
La seule difficulté est de justifier l'unicité du carré :
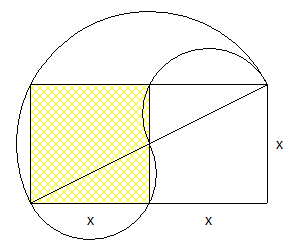
Avec Pythagore : 5x²=40 000 donc A=x²=8 000 mm² .
Vasimolo
#17 - 17-12-2014 17:58:20
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Le carrré caché
8000 mm² ? (sans pourtant être sûr de son existence...)
#18 - 17-12-2014 23:27:31
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Le carréé caché
La première figure illustre mon cheminement pour résoudre le problème.
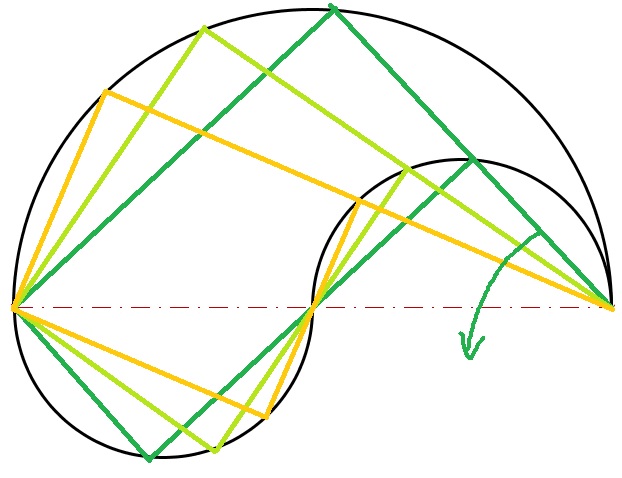
J'ai pensé au triangle rectangle inscrit dans un demi-cercle.
En partant du point à droite, j'ai tiré un trait vert au hasard puis j'ai complété grâce aux 3 demi-cercles les triangles rectangles (sans repasser les hypoténuses en pointillés rouges discontinus), ce qui m'a donné le 1er grand rectangle vert.
Pour en réduire la surface et m'approcher du carré, j'ai ensuite fait pivoter le 1er segment vert comme l'indique la flèche, et j'ai obtenu un rectangle plus proche du carré.
Le troisième rectangle est "allé trop loin", il y avait donc une position optimale donnant le carré.
Voici le dessin de cette position qui donne le carré, dont j'ai pris comme côté "a".
les 2 petits cercles étant symétriques par rapport à F, on a F au milieu de [DE] donc DF = a/2
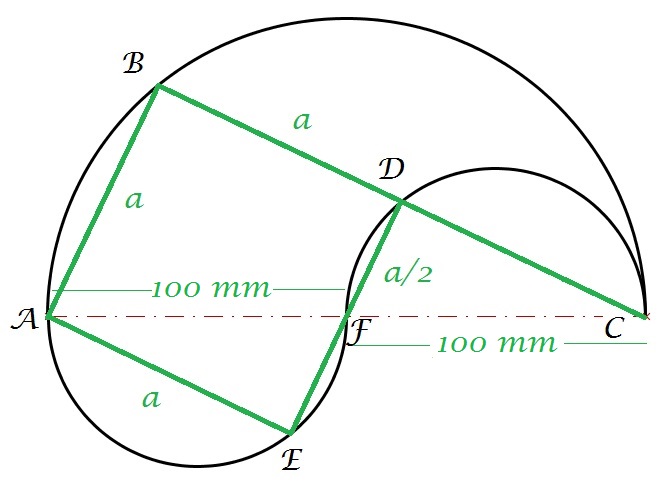
D'après la droite des milieux, D milieu de [BC], donc DC = BD = a
Dans DCF : L'angle en C vaut Atan(a/2/a)=Atan(1/2)
Ensuite cos C = a/100 donc a = 100 cos(Atan(1/2)) = 100/√(1+(1/2)²) = 200/√5
Enfin L'aire du carré vaut a² = 200²/5 = 8000 mm²
#19 - 18-12-2014 09:44:29
- unecoudée
- Professionnel de Prise2Tete
- Enigmes résolues : 0
- Messages : 319
Lee carré caché
salut.
je reprend le dessin de golgot.
je sais que le point F est le centre de symétrie des 2 petits demi cercles .
si je trace un carré ABDE , les points A & B appartenant au grand cercle et DE sur à la droite horizontale passant par F . La verticale passant par F est aussi médiane du carré.
En appliquant Pythagore on a immédiatement la relation :
R² = 10000 = 5/4.x² entraine x² = 8000
F étant le centre du grand cercle et aussi le centre de symétrie des 2 petits cercles ; C est d'une autre part le centre d'homothétie de 2 cercle dont le rapport est 1/2
il suffit d'effectuer une rotation du carré autour de F et d'aligner A , F & C
puisque x² = BC . EF
merci d'avoir participé et pour vos beaux dessins.
#20 - 24-12-2014 23:37:13
- Dinology
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 1
#21 - 24-12-2014 23:52:50
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
le varré caché
20 élèves de cm2 ? 
Mots clés des moteurs de recherche
|
 |
|
Prise2Tete
Forum
Statistiques
Liste des membres
Hall of Fame
Contact
|

 Accueil
Accueil
 Forum
Forum