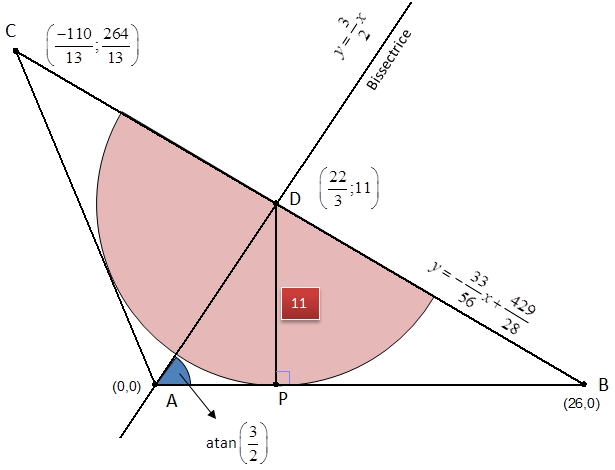
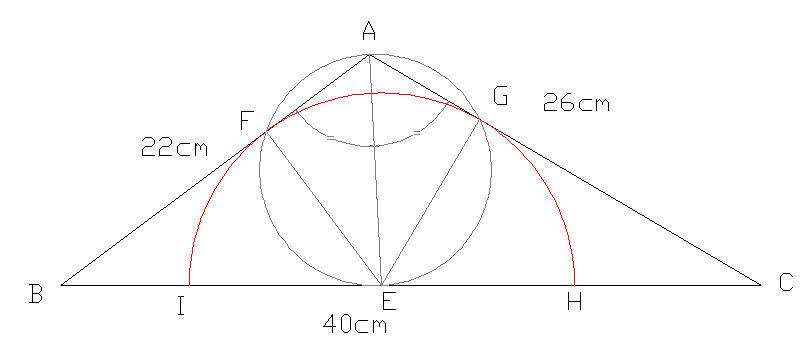
Soit O le centre du demi cercle P le point de tangence sur [AC] et Q sur [BC]
alors les triangles OPA; OPC; OQC et OQB sont rectangles
on note x = CP et z = CB et OA = y et R le rayon du cercle

d'après le théorème de Pythagore
OC²=x²+R²
OC²=z²+R²
y²=R²+(22-x)²
(40-y)²=R²+(26-z)²

donc x²=z² et donc z=x et on exclut z=-x

d'où (40-y)²-y²= (26-x)²-(22-x)²
donc 40(40-2y)= ((26-x)-(22-x))((26-x)+(22-x)=4(48-2x)

et d'où 10(20-y)=24-x
x=24-200+10y=10y-176

d'après le théorème d'Al Kashi
BC²=AB²+AC²-2*AB*AC cos(A)
cos A= (AB² + AC² - BC²) /2*AB*AC=(40² + 22² -26²)/2*40*22=0.8
et donc OC²=y²+22²-2*22*0.8*y=y²-35.2y+484

d'où y²-35.2y+484=(10y-176)²+R²
et R²=y²-(198-10y)² d'où -35.2y+484=(10y-176)²-(198-10y)²=22(20y-374)

d'où -1.6y+22=20y-374 donc y=55/3 donc x=22/3 et donc R²=(55/3)²-(44/3)²
donc R²=1089/9=121 donc R=11 et on exclut R=-11

Pas trouvé plus simple que par la géométrie analytique...

(...)

En utilisant l'indice :

44 est le demi périmètre

L'aire du triangle = [latex]sqrt{44(44-22)(44-26)(44-40)}=264[/latex]

Or aire ABC = aire CDA + aire BDA =  [latex]\frac{22R}{2}+\frac{26R}{2} = 24R[/latex]  (R est le rayon du demi-cercle)

Si 24R = 264, alors R = 264/24 = 11

Merci pour le coup de pouce Vasimolo

Trois bonnes réponses : scablor , looozer et franck .

La justification est très courte si on si prend bien . Scablor est le seul à l'avoir vue pour le moment

Indice : Spoiler : [Afficher le message] l'aire du triangle est 264 cm²

Vasimolo

Utilisant la formule de Héron d’Alexandrie, l’aire du triangle, [latex]A_1[/latex], peut se calculer:
[TeX]s_1 = \frac{a+b+c}{2}=48[/TeX][TeX]A_1 = sqrt(s_1(s_1-a)(s_1-b)(s_1-c))=264[/TeX]
Par symétrie, le demi-gâteau inscrit dans ce triangle est un cercle inscrit dans un rectangle particulier en forme de cerf-volant (« kite » pour une recherche sur site en anglais).

Ce type de rectangle se caractérise entre-autre par l'existence d'un cercle inscrit ainsi qu'une relation bien utile ici:
si [latex]A_2[/latex] est l'aire du kite, [latex]s_2[/latex] son demiperimètre et r le inradius (rayon du cercle inscrit)

[latex]r=\frac{A_2}{s_2}=\frac{2A_1}{(22+26)}=11[/latex] cqfd

Bon on a pas mal ramé avec celui-ci , c'est curieux car j'étais vraiment persuadé que vous n'en feriez qu'une bouchée

Beaucoup de bonnes réponses malgré tout mais seul scrablor a tout de suite vu  l'astuce . Bon , La géométrie c'est vraiment plein de pièges et il m'arrive de sécher misérablement sur des petits exercices 6ème

Il fallait en effet calculer l'aire avec la formule de Heron puis remarquer que le rayon de la tarte constituait une hauteur de chacune des parts obtenues en traçant la bissectrice ( la droite passant par le centre du demi-disque et le sommet opposé du triangle ) .

La figure du SingeMalicieux illustre bien le résultat

Vasimolo

PS : Je comptais arrêter la série ici mais comme Gabriel nous fait une relance , je crois que c'est reparti pour une petite série . Dommage car j'ai plein de problèmes avec des dés , des cartes , des quadrillages qui devront attendre encore un peu