Soient :
- a l'arête du cube (formé par 14 gâteaux)
- Vp le volume d'une part (d'un gâteau)

On a :  14x7xVp  = a^3

a est entier. Vp doit être entier, car les parts sont des parallélépipèdes de longueur, largeur et hauteur entières.

Les plus petites possibilités sont :
a = 14 ; Vp = 28 = 2^2 x 7
a = 28 ; Vp = 224 = 2^5 x 7
a = 42 ; Vp = 756 = 2^2 x 3^3 x 7

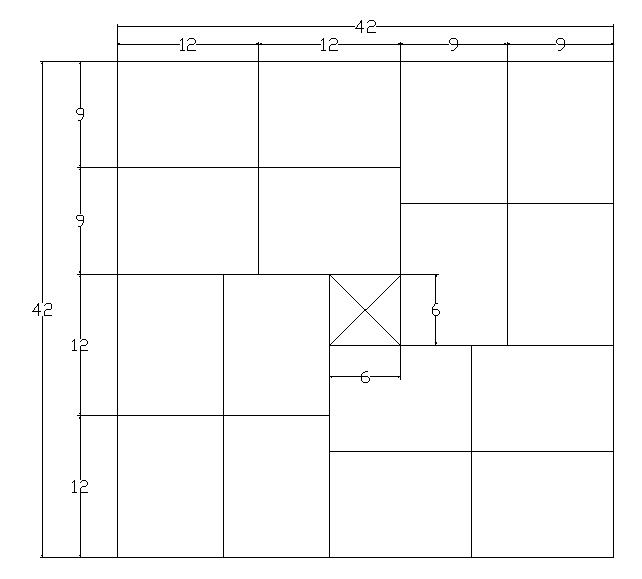
Or, les parts sont de hauteur 7, et leurs largeur (l) et longueur (L) doivent respecter l'égalité 4.l = 3.L (vu l'agencement des parts sur l'image).
Les deux premières possibilités ne nous donnent pas l et L entiers.
La troisième possibilité nous donne des parts de taille h=7, L=12 et l=9 !

...et donc un gâteau de 36x21x7cm.

7 parts identiques forment un gâteau  qui est fait 7 cm d’épaisseur. Le volume total de la grosse gourmandise est donc de 7x7xAxB avec A et B étant les arêtes d’une part. Une fois arrangés, les 7 parts de 14 gâteaux peuvent former un cube de cote C. Ainsi 14x7×7AB=C^3

Le volume d’une seule part de gâteau est donc 7AB ou encore C^3/98. A, B et C sont des valeurs entières. AB est donc entier ce qui implique C^3/98 aussi.
Pour qu’il soit possible de découper un gâteau en 7 parts identiques, comme le montre le Vasimolo’s schéma, 4A=3B

Ceci donne, A=3B/4 et 7AB=C^3/98 => B^2=4C^3/2058. La première solution est B=12 ce qui est déjà une sérieuse part de gâteau. Le volume d’une part est donc 7x9x12=756cm3 ou 2814 kcal pour une recette légère.

Le gâteau entier mesure 21x36x7, une belle pièce !

Nous voilà maintenant avec 98 parallélépipèdes de 7x9x12cm pour arranger en un cube de 42cm de côté. Moi qui n'aimais déjà pas les gâteaux…

J'avoue ne rien comprendre à l'énoncé... Je ne suis pas à l'aise non plus avec l'ésotérisme

Il y a 1 gâteau ou 14 gâteaux? En quoi peut-on se fier au dessin? Je nage complètement

Pour les deux questions super-top-bonus inspirées par mon bon voisin Vôôgien, je vais, comme j'en avais l'habitude lorsqu'une énigme me plaisait beaucoup, répondre en image.



PS : A noter que j'ai fait cela de façon intuitive, et que je n'ai pas cherché de démonstration mathématique (et que donc je peux me tromper).

PPS : A noter que je viens de me rendre compte (en relisant mon post avant de l'envoyer), que je me suis planté sur la compréhension de la première question ultra-supra-bonus de scrablor. Mais vu qu'il reste encore une cinquante d'heures pour la résoudre, cela peut faire l'objet d'une nouvelle question maxi-top-bonus ! A toi de voir Vasimolo
Celle-ci pourrait commencer par "Si on coupe les quatorze gâteaux de façon identique..."

PPPS : A noter que vivent les gâteaux, et vive P2T !!!

PPPPS : A noter que le matheux du site (non MthS je ne te dénonce pas), boude les gâteaux. Faudrait ajouter du rhum dedans pour qu'il s'y intéresse je pense

PPPPPS : A noter que je vais continuer de réfléchir à la question 1 de scrablor

PPPPPPS : T'as vu kosmo ? Moi je ne floode pas, je rajoute tout ce que j'ai à dire dans le même post

PPPPPPPS : Cette dernière remarque vaut également pour MthS

96 parts peuvent être arrangées telles quelles en 6 tranches de 7cm d’épaisseur. Ceci laisse deux parts à découper pour insérer dans le trou de 6x6 au milieu. Le 7x9x12 devient deux 7x6x6 et deux 7x3x6 qui se glissent au centre du monument.



Alternativement, le gâteau pourrait être découpé en 6 parts égales, tant pis pour la symbolique, de 21x6cm sur toujours 7cm d’épaisseur. Ces parts s’arrangent facilement pour former le cube demandé.

Allez pour un bonus 4°)

4°) On part des 14 gâteaux déjà découpés en 7 parts égales comme sur le modèle . Quel est le nombre minimal de coupes à pratiquer pour reconstituer le cube ?

Les meilleures réponses déjà fournies .

Bonus 1 : schaff avec 84 parts ( on doit pouvoir faire mieux ) .
Bonus 2 : LeSinge et schaff 24 parts ( on doit pouvoir faire mieux ) .
Bonus 3 : LeSinge 28 parts ( on ne peut pas faire mieux ) .
Bonus 4 : franck 104 ( seulement deux parts coupées , difficile à battre ) .

Avis aux amateurs

Vasimolo

Pour le bonus 1, je ne fais pas mieux que schaff avec 84 parts.
Pour cela, je découpe mes gâteaux comme dans ma démonstration du bonus 2 (voir mon précédent post).

Pour le bonus 4, je suis sur le problème ! Les coupes doivent-elles être entières ?

Vasimolo a écrit:

Bonus 4 : franck 100 ( seulement deux parts coupées en deux , difficile à battre )

Superbe résultat
J'ai hâte de le voir !

De mon côté, je ne fais pas mieux que 104 parts...

Ah bon ?
Alors je vous présente ma démo pour le bonus 4. Je pensais vraiment être hors course.

Désolé de vous obliger à chausser des lunettes, mais je tâche à ne pas faire un post de 15km de haut. (déjà qu'il en fait 10...)

Un sujet qui vous a bien inspiré

Il fallait voir que la largeur d'une part était les 3/4 de la longueur et le reste venait tout seul .

Peut-on améliorer les résultats des bonus ???

Merci pour la participation et les jolis dessins

Vasimolo