 |
#1 - 07-07-2010 20:29:28
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâyeau 12
Un petit gâteau aux fruits pour se reposer :
Depuis que le nouvel apprenti sévit chez le pâtissier du coin , les gâteaux ont des formes vraiment bizarres . J'avais commandé un poirier pour six et j'ai reçu une vague chose de forme triangulaire .

Pour le partager , j'ai relié chaque sommet au milieu du côté opposé . J'ai bien six parts mais sont-elles toujours égales ?
Bonne dégustation !!!
Vasimolo
#2 - 07-07-2010 20:45:15
- emmaenne
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3073
- Lieu: Au sud du Nord
Gâteau 122
moi je vois 6 parts et tu parles de 4 parts, comment veux-tu que je m'en sorte 
Dans le cadre de la quinzaine du beau langage, ne disez pas disez, disez dites. (Julos Beaucarne)
#3 - 07-07-2010 21:00:08
- scrablor
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 965
gâtzau 12
Application classique du théorème de Thalès et de la position du centre de gravité aux deux tiers de la médiane en partant du sommet...
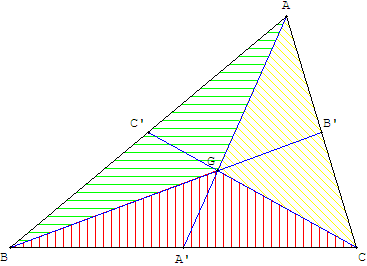
Le triangle rouge a même base que ABC et une hauteur réduite au tiers car GA'=AA'/3.
Ainsi : aire(BGC)=aire(BAC)/3.
La position de A' au milieu de [BC] donne aussi : aire(BGA')=aire(BGC)/2.
Par suite : aire(BGA')=aire(BAC)/6.
Il en est de même pour les cinq autres petits triangles.
Bon appétit 
Celui qui fuit les casse-tête ne vaut pas un clou.
#4 - 07-07-2010 21:04:01
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Gâteau 1
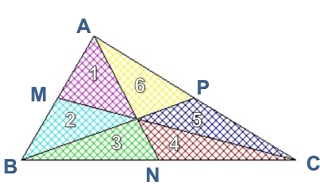
Dans chaque paire 1-2 , 3-4 et 5-6, les triangles ont même aire puisqu'il ont même base (BN=NC) et même hauteur (sommet commun).
Les triangles BMC et BPC ont aussi même base et même hauteur puisque MP||BC, on en déduit que BMP-(3+4) = BPC-(3+4) et donc 2=5. Même raisonnement pour montrer que 1=4 et que 3=6.
Les 6 triangles ont donc la même aire.
#5 - 07-07-2010 21:22:24
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
Gâteau 1
oui
triangle ABC, de milieux a,b,c (a opposé de A, b opposé de B et c opposé de C), et O centre du triangle (croisement des médianes)
On note S(xyz) l'aire du triangle xyz.
comme a milieu de BC, S(OaB) = S(OaC)
de meme S(OcA)=S(OcB) et S(ObA)=S(ObC).
(En d'autres termes, les petits triangles cotes à cotes qui partagent un coté du gros triangle sont de meme aire)
De plus, S(AaB)=S(AaC) (les deux moitiés du gros triangle issu de A et coupé au milieu sont de meme aire)
et en developpant chaque coté il vient :
S(OcA) + S(OcB) + S(OaB) = S(ObA) + S(ObC) + S(OaC)
qui se simplifie en S(OcA)=S(ObA),
et par symétrie (de rôle joué, pas dans la figure), on a l'égalité pour tout le monde...
#6 - 08-07-2010 00:41:45
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#7 - 08-07-2010 02:45:34
- chaton_endormi
- Amateur de Prise2Tete
- Enigmes résolues : 0
- Messages : 2
Gâteau 2
Affirmation : Les 6 parts d'un triangle (non-aplati) découpé par ses médianes sont d'aires égales.
1°) C'est évident par symétrie si le triangle est équilatéral.
2°) Si c'est vrai pour un triangle T, c'est vrai pour tout triangle f(T) où f est une transformation affine du plan.
En effet, f conserve les milieux et les segments ( f[AB] = [f(A)f(B)] ) donc f envoie un triangle et ses médianes sur un triangle et ses médianes.
De plus, f multiplie les aires par une constante non-nulle, donc conserve les égalités d'aires.
3°) Pour tout triangle non aplati, il existe un triangle équilatéral T et une application affine tel que f(T) soit ce triangle-là.
(Car les transformations du plan agissent transitivement sur les triangles non aplatis.)
Ce qui prouve l'affirmation.
Par conséquent, les six convives auront bien tous autant à manger.
#8 - 08-07-2010 08:30:14
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
Gâtaeu 12
J'ai une démonstration assez rapide. Comme le ratio entre les différentes aires reste inchangé par une transformation linéaire, on peut transformer ce triangle en triangle équilatéral, pour lequel les aires sont manifestement égales :
*On peut même juste s'arrêter à l'isocèle du dessin, ca suffit pour généraliser.
#9 - 08-07-2010 08:34:24
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
fâteau 12
sinon le calcul direct donne aussi la réponse, puisque l'aire d'un petit triangle est
s = l * h / 2 (où s l'aire, l la largeur, et h la hauteur du petit triangle)
s = L/2 * H/3 / 2 (où L la largeur, et H la hauteur du grand triangle)
s = (L*H/2) / 6 = S / 6 (où S l'aire du grand triangle)
#10 - 08-07-2010 10:18:59
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Gâteau 112
Les parts sont toujours égales.
Cela est du à l'utilisation des médianes.
Je numérote les surfaces comme ci-dessous:
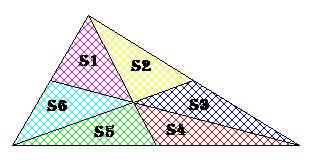
On raisonne sur l'égalité des surfaces. La surface d'un triangle est égale (par exemple) à (la base x la hauteur)/2. Si on considère S4 et S5, elles sont égales car la hauteur des 2 triangles est la même et la base aussi (puisque le point du bas est le milieu du segment).
Le même raisonnement donne: S1+S6+S5=S2+S3+S4 et comme S4=S5, S1+S6=S2+S3. Encore le même raisonnement donne S1=S6 et S2=S3 donc l'égalité précédente donne 2S1=2S2 par exemple donc S1=S2=S6=S3 et séparément S4=S5.
En utilisant S4+S5+S6=S1+S2+S3, en simplifiant par S6 et S3 par exemple puisqu'ils sont égaux, et en appliquant les égalités déjà connues, on obtient, 2S4=2S1 donc S1=S2=S3=S6=S4=S5.
CQFD.
J'ai trouvé ce gâteau la plus digeste que certains autres  Merci. Merci.
#11 - 08-07-2010 10:50:32
- emmaenne
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3073
- Lieu: Au sud du Nord
gâtzau 12
mauvaise foi peut-être mais bon foie 
Dans le cadre de la quinzaine du beau langage, ne disez pas disez, disez dites. (Julos Beaucarne)
#12 - 08-07-2010 13:01:36
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Gâteaau 12
Je dirais oui.
Ca se démontre par la surface d'un triangle qui est égal a sa base fois sa hauteur sur 2. Du fait que l'on coupe entre un sommet et le milieu de la base d'un triangle, chaque coupe divise un triangle en 2 partie égales, quelque soit la position du sommet, pour a la fin avoir 6 petits triangles a surfaces égales.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#13 - 08-07-2010 15:47:27
- gabrielduflot
- Expert de Prise2Tete
- Enigmes résolues : 34
- Messages : 614
gâtrau 12
oui
Si ABC est un triangle et A'; B' et C' les milieux des côtés des côtés [BC],[AC] et [AB] alors (AA'); (BB') et (CC') sont les 3 médianes et G le centre de gravité alors les triangles ABG et ACG et BCG sont de même aire.
d'où (GC') est donc une médiane du triangle ABG et donc l'aire du triangle AGC' est égale à l'aire du triangle GBC' et de même pour les triangle GBC et GAC
#14 - 08-07-2010 23:16:05
- dylasse
- Professionnel de Prise2Tete
- Enigmes résolues : 21
- Messages : 381
Gâetau 12
Je dirais : OUI.
Une médiane issue de A sépare un triangle en 2 morceaux de mêmes surface (on peut le "sentir" en faisant des bandes étroites parallèles au coté BC qui sont coupées en 2 par la médiane ou bien l'affirmer car la surface du triangle c'est base x hauteur / 2).
Si on appelle H, I, J, K, L et M les surfaces des six parts du gateau (H bleu, I rose etc...).
L'application de la règle ci-dessus donne H = I, J = K et L = M.
De plus, H+I+J = K + L + M et I + J + K = L + M + H donc H = K et de la même façon I = L et J = M.
Donc tout le monde ils sont égaux !!!!
#15 - 09-07-2010 09:51:05
- Nicouj
- Professionnel de Prise2Tete
- Enigmes résolues : 27
- Messages : 330
Gâteau 112
Une médiane coupe le triangle original en 2 triangles contenant 3 parts chacun.
Ces deux triangles ont en commun au moins 2 cotés : la médiane et la moitié de la base dont la médiane est issue.
Le troisième coté de chacun des deux triangles est un des deux autres cotés du triangle. Ces 2 demi triangles ont la même aire ssi leur troisieme coté sont égaux.
Donc les six parts ne peuvent pas être de même surface si le triangle n'est pas équilatéral.
Si il l'est alors les parts sont trivialement de même surface, donc de même aire.
Finalement les 6 parts sont égales ssi le triangle est équilateral.
#16 - 11-07-2010 00:57:26
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#17 - 11-07-2010 12:15:23
- Nicouj
- Professionnel de Prise2Tete
- Enigmes résolues : 27
- Messages : 330
GGâteau 12
vi je me suis bien planté  . .
Un copain me l'a fait remarqué vendredi et m'a aidé a comprendre mon erreur.
Je me basait sur la formule de Héron pour le calcul d'aire de triangle quelconque.
[latex]\sqrt{p(p-a)(p-b)(p-c)}[/latex] avec a, b, c les cotés et p le demi périmètre.
Je m'étais dit que si juste un coté change alors un seul facteur du produit change et donc le résultat change.
En fait j'ai oublié que si un coté change alors p aussi et donc les autres facteurs changent aussi mais pas forcément le résultat ><.
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum











