Avec 7 caches, je recouvre entièrement le gateau (un centré + 6 dont les diamètres sont les cordes de l'hexagone inscrit dans mon gateau), je recouvre donc les 91 cerises.
Si aucun cache ne recouvre plus de 11 cerises, alors les 7 ne recouvrent que 70 cerises au maximum : contradiction.
Le patissier n'a donc pas moyen de disposer 91 cerises de telle sorte que 11 d'entre elles ne puissent être recouvertes par un disque.



Remarque : si on considère que les cerises ont une épaisseur, on peut supprimer les 12 points du recouvrement à 7 caches qui ne sont recouverts que par le perimètre d'un cache en en rajoutant un huitième (on a toujours 91/8>=11).



Remarque 2 : d'après ma réponse, 71 cerises auraient été suffisantes pour ruiner notre patissier... alors, est-ce une erreur d'énoncé de Vasimolo, une erreur de résolution de Dylasse ou un piège de Vasimolo qui n'a pas pris le nombre optimisé pour nous faire cogiter un peu plus !!!

Je ne vois pas comment il peut faire ça avec plus de 70 cerises si le masque est pour 11.

Sur le pourtour, on ne peut pas mettre plus de 10 cerises sur un arc quelconque d'angle 60°,
soit 60 cerises au total, sinon il existerait une position où un masque couvrirait 11 cerises.

Quelque soit la répartition sur les arcs de 60°, il ne reste plus qu'une très petite zone au centre, qui peut recevoir un maximum de 10 cerises, le total est 70.

Si le masque était pour 14 cerises, alors on pourrait mettre 91 cerises en 7 groupes de 13,
6 groupes sur 6 arcs de 60°, et 1 groupe au centre.

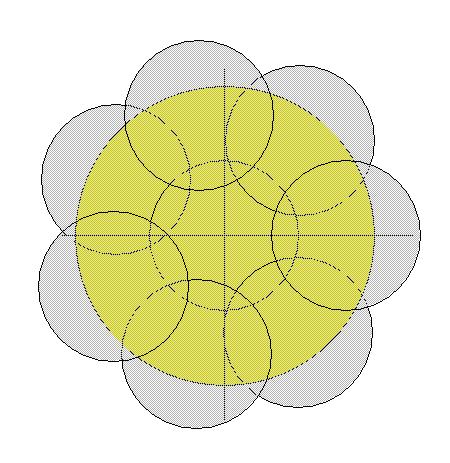
Lemme : on peut placer placer 9 petits disques qui recouvrent l'intégralité du grand disque

Si on arrive à démontrer ce lemme, alors en plaçant 10 bougies maximum par disque, on arrive à mettre au plus 90 bougies sur le gâteau. Mais la 91ème sera forcément dans une des 9 régions, et on aura alors une région avec 11 bougies, ce que refuse le pâtissier !
La chose est donc impossible

Démonstration du lemme :
Je suis en train de faire une figure : on trace l'hexagone inscrit dans le grand disque de côté le rayon du grand disque. 6 disques auront chacun pour diamètre un côté de l'hexagone, et les 3 autres auront pour diamètre les segments reliant un sommet de l'hexagone au centre du grand disque (on prend un sommet sur 2).
Ca sera plus clair avec une vraie figure ...

... que voici !



EDIT
Et ton message me confirme qu'on peut faire mieux, je m'en doutais, mais je suis contenté de trouver 9 zones, comme tu parlais de 91 bougies
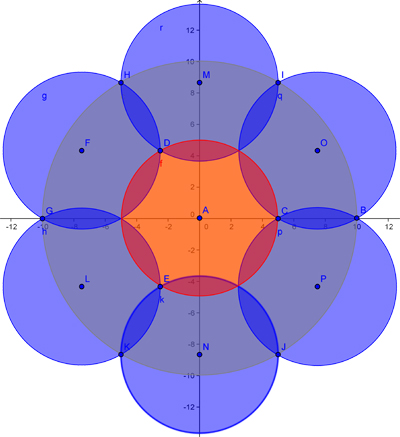
La question serait donc de savoir quel est le nombre minimum de disques de 5cm de diamètre permettant de recouvrir le grand disque ... Moins que 9, apparemment
La figure suivant montre qu'on peut le faire avec 7 zones. Je ne pense pas qu'on puisse faire mieux, mais je n'en suis pas sûr !

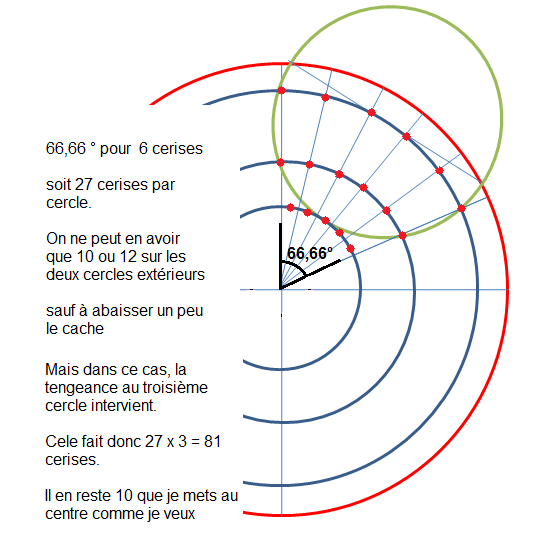
En fait l'angle de 66, 66 ° est choisi car la marge de manoeuvre est entre 60° et environ 70° ( tangentes au cache ) Entre ces deux valeurs, il n'y en a que 4 qui permettent cette solution, de manière à ce que la dernière cerise retombe sur la première :

Alpha / 5 doit être un diviseur entier de 360

ce qui laisse 360 x5 /alpha entier avec alpha compris entre 60 et 70 ce qui laisse le choix entre 26, 27, 28, ou 29 cerises par cercle.

Un petit bilan

Dylasse & Halloduda : parfait !
Oups : ne cherche pas trop compliqué le temps alloué à l'énigme est réservé à des prolongations ( au cas où ) .
007 : juste , on peut encore faire mieux
Franky et Gwen : je ne suis pas convaincu

Vasimolo

J'aurais tendance à dire que ça n'est pas possible.
C'est approximatif mais voilà :
Soit une configuration des bougies.
Soit C le grand cercle (le gâteau), et E l'ensemble des cercles inscrits dans C, et soit b(c) = nombre de bougies cerises couvertes par c pour c€E.

Examinons m=max b(c) (pour c€E), autrement dit, m est le plus grand nombre de bougies capturées dans un cercle c pour la configuration courante.
On souhaite que m soit inférieur à 11, or m est minimal (?) quand tous les b(c) sont égaux à la moyenne attendue (l'idée étant que si un c en couvre moins que la moyenne, un autre devra en couvrir plus).
Or, la moyenne est donnée par (bougies/surface de C) * (surface de c), soit 91/(pi.R^2)*(pi.r^2) avec R=10 et r=5, soit 91/4=22,75 bougies


Soit dC la densité moyenne de cerises sur le gâteau (dC=91/(pi.R^2)) et d(c) celle sur un c€C quelconque (d(c)=b(c)/(pi.r^2)).
Il est impossible que pour tout c, d(c)<dC sinon les c€E ne recouvrirait pas toutes les cerises (ça me paraît évident mais y a un trou là).
Donc il existe au moins un c0 tel que d(c0)>=dC.
Mais alors, b(c0)=d(c0).pi.r^2>=dC.pi.r^2=91/(pi.R^2).pi.r^2=22,75 : près du double de ce qu'il faudrait !?

Addendum :
E ne contient pas E' l'ensemble des cercles non-inscrits dans C (ceux qui chevauchent), mais si on les considère, il existe a fortiori au moins un c0 tel que d(c0)>=dC. Ca ne change pas le résultat d'impossibilité.

lol oui, pourquoi je parle de bougies moi ?

Bonus diamètre 3.80 m, masque 5 cm.

Avec une structure de cercles concentriques comme dans le problème initial,
23872 cerises, la structure n'est pas adaptée.

Sauf erreur de calcul, je ne dépasse pas 26610 cerises avec une structure hexagonale
symétrique, avec cerise au centre.

Y a pas une autre boulangerie dans ton patelin ?

L'approche précédente donne 10,38 comme quantité moyenne de cerises pour chaque c, comme par hasard... avec dC~0,53 cerise/cm2


Une question me brûle les lèvres, les cerises ont-elles une surface ? Ou, est-il possible de couvrir 10 cerises plus une demi par exemple ?

Toujours pas possible ?

Si c'était possible et si les cerises sont des points, alors la densité de 10,4 ne peut être atteinte en couvrant des morceaux de cerises, chaque cercle c couvre donc au plus 10 cerises (puisqu'il faut arrondir), mais alors chacun a une densité moyenne d'au plus 10/(pi.r^2) et donc (?) la densité moyenne sur tout le gâteau est aussi inférieure à 10/(pi.r^2) ce qui permet 10/(pi.r^2)*(pi.R^2)=57760 cerises, pas plus.

Parce que c'est une surface convexe. J'imagine que ça doit se déduire d'un truc connu que je ne connais pas.

J'avoue que le passage de "pour tout disque c, la densité est <= d" à "la densité est <= à d sur tout le grand disque" est une question très intéressante et qui me turlupine. Je ne trouve rien de tout fait et ne vois pas très bien comment faire en général...

@Gasole

Tu peux copier 100 fois : "Des cerises c'est pas des bougies" 

Vasimolo