Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 06-08-2010 00:07:02
Gâtea u22Apparemment il liquide les boîtes aux formats bizarres .
#0 Pub#2 - 06-08-2010 02:17:47
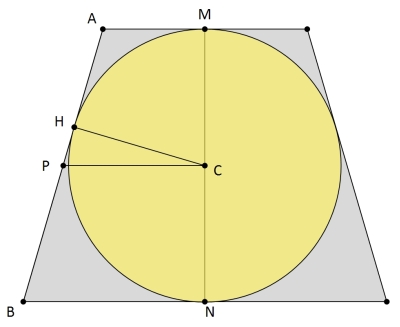
Gâtea u22Soit ABCD le trapèze isocèle tel que AB=18cm et CD=32cm et E le point d'intersection des droites (AD) et (BC) pour former ECD un triangle isocèle. #3 - 06-08-2010 11:33:30
gâtzau 22
#4 - 06-08-2010 12:15:55
Gâtaeu 22Partant d'un point A extérieur à un cercle, on peut mener deux tangentes telles que AT = AT'. Cette propriété permet d'obtenir les longueurs des deux côtés non cotés du trapèze : 9+16=25. Celui qui fuit les casse-tête ne vaut pas un clou. #5 - 06-08-2010 14:00:01
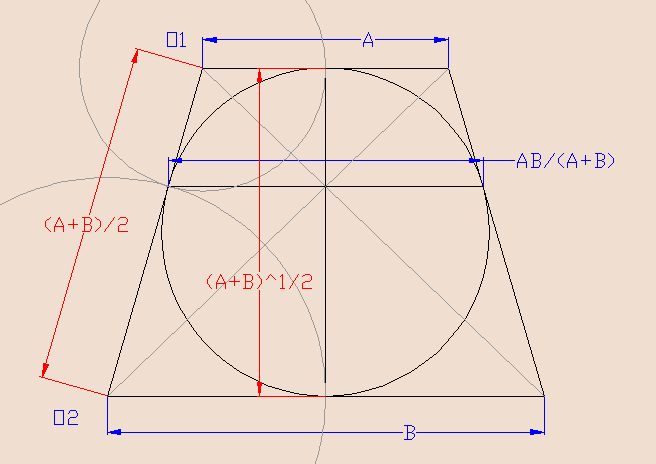
Gâetau 22Si on dessine la figure autrement, on a : #6 - 06-08-2010 17:35:14
gâtzau 22
The proof of the pudding is in the eating. #7 - 06-08-2010 19:36:12#8 - 06-08-2010 20:04:26
Gâtaeu 22Ceci est sans doute lié à la constante qualité de ces énigmes The proof of the pudding is in the eating. #9 - 08-08-2010 20:11:33
Gâteau 222WOW ! Elle m'aura donné du mal celle-ci ! Avoir quatre mains, c'est plus pratique pour taper sur un clavier. #10 - 09-08-2010 00:20:12
âteau 22J'avais fait autrement mais bon la richesse naît de la diversité : Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.