|
#1 - 27-02-2014 10:35:31
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
gâteay 73
Bonjour à tous 
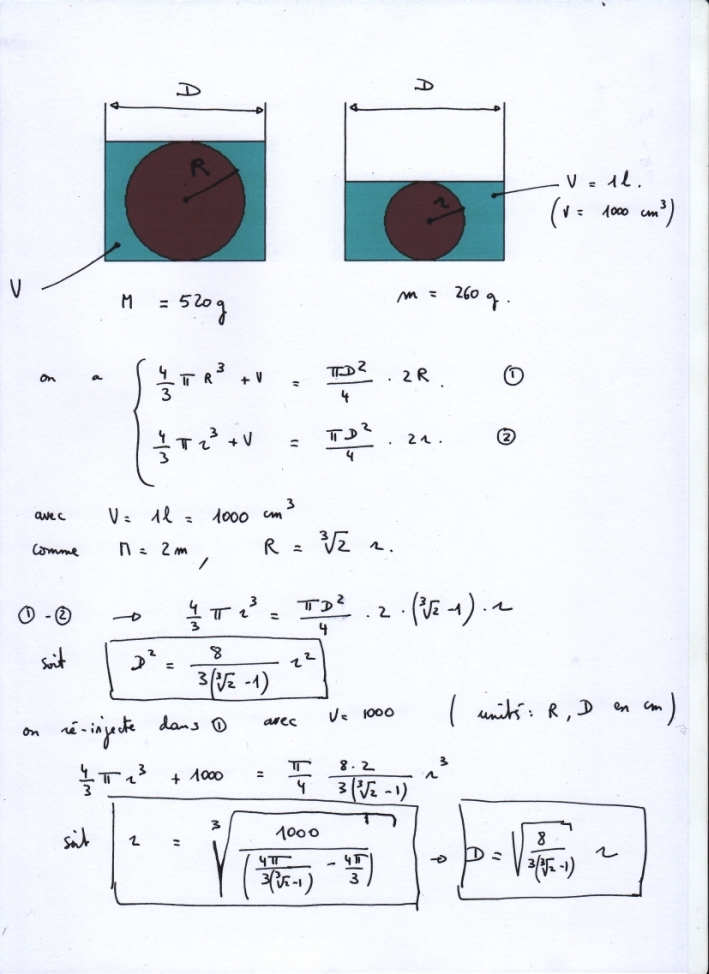
Depuis quelques jours mon pâtissier amuse la galerie avec un jeu de sa conception . Il a réalisé deux boules avec le même chocolat , une de 260 g et l’autre de 520 g . Il les présente à son public ainsi qu’un bocal cylindrique vide et un pichet d'un litre d’eau . Il demande ensuite à un client de choisir une des boules de la déposer au fond du bocal , de vider le pichet par dessus et de constater que miraculeusement l’eau affleure au sommet de la boule .

Pourtant il est clair que les deux boules n'ont pas la même taille , comment fait-il ?
Vasimolo
La case réponse valide le diamètre du bocal en cm sous la forme **.******
Amusez-vous bien 
#2 - 27-02-2014 18:12:18
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
gâtzau 73
Edit : bon ben j'ai pas mes formules TeX... Bon le résultat est d=2/((pi*sqrt(6*(2^(1/3)-1))*(2-2^(1/3))))^1/3, soit environ 14.019157 cm
La première boule a un rayon [latex]r_1[/latex] (exprimé en décimètres) et un volume [latex]v_1 = \frac{4}{3}\pi {r_1}^3[/latex] (exprimé en décimètres cubes, donc en litres)
La seconde boule a un rayon [latex]r_2[/latex] et un volume [latex]v_2 = \frac{4}{3}\pi {r_2}^3[/latex].
Avec le même volume massique, pour une masse 2 fois plus élevée on a un volume 2 fois plus élevé aussi.
Par conséquent, [latex]2v_1=v_2[/latex] et donc [latex]r_2 = r_1\sqrt[3]2[/latex]
Soit un bocal cylindrique de diamètre [latex]d[/latex], un volume arrivant à la hauteur [latex]h[/latex] du bocal représente une valeur de [latex]\frac{1}{4}\pi d^2h[/latex]
La première boule, avec un litre d'eau, représente un volume qui monte à une hauteur de [latex]2 r_1[/latex], le volume est donc de [latex]\pi \frac{d^2}{2}r_1[/latex]
On a donc [latex]\pi \frac{d^2}{2}r_1 = \frac{4}{3}\pi {r_1}^3 + 1[/latex]
Idem pour la seconde boule, où [latex]\pi \frac{d^2}{2}r_2 = \frac{4}{3}\pi {r_2}^3 + 1[/latex]
On peut même remplacer [latex]r_2 = r_1\sqrt[3]2[/latex] pour avoir
[TeX]\pi \frac{d^2}{2}r_1\sqrt[3]2 = \frac{8}{3}\pi {r_1}^3 + 1[/TeX]
Système:
[TeX]\pi \frac{d^2}{2}r_1 = \frac{4}{3}\pi {r_1}^3 + 1\\
\pi \frac{d^2}{2}r_1\sqrt[3]2 = \frac{8}{3}\pi {r_1}^3 + 1[/TeX]
Par soustraction:
[TeX]\frac{3}{8}\frac{d^2}(\sqrt[3]2-1) = {r_1}^2[/TeX]
et au final
[TeX]r_1 = d\sqrt{\frac{3}{8}(\sqrt[3]2-1)}[/TeX]
On remplace :
[TeX]\pi \frac{d^3}{2} \sqrt{\frac{3}{8}(\sqrt[3]2-1)} = \frac{4}{3}\pi d^3 \sqrt{\frac{3}{8}(\sqrt[3]2-1)}^3 + 1[/TeX]
En ne laissant que la constante à droite, on obtient [latex]d^3 \frac{\pi}{4} \sqrt{\frac{3}{2}(\sqrt[3]2-1)}(2-\sqrt[3]2) = 1[/latex]
On ne garde que le diamètre à gauche, on arrange un peu, et voilà : [latex]d= \frac{2}{\sqrt[3]{\pi\sqrt{6(\sqrt[3]{2}-1)}(2-\sqrt[3]{2})}}[/latex]
#3 - 27-02-2014 18:17:44
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
Gâtaeu 73
Demandes-tu le diamètre intérieur ou extérieur de ton bocal  ? ?
Par ailleurs, je suis très étonné que ton pâtissier arrive à se faire fabriquer un bocal avec une précision de cent angströms  ! !
Ceci dit, je suis très admiratif devant son inventivité  ! !
Spoiler : [Afficher le message] Blague à part, je trouve un diamètre de 14,0191571 cm,qui ne valide pas la case réponse  ... ...
Le rayon de ma petite boule de chocolat est de 4,3768157 cm, son volume de 351,2071926 cm3.
Celui de la grosse, de 5,5144423 cm, avec un volume de 702,4143852 cm3.
Et je trouve bien un volume total (eau + chocolat) de 1351,2071926 cm3 pour la petite boule et de 1702,4143871 cm3 pour la grosse... j'ai surement dû faire une erreur  . .
#4 - 27-02-2014 18:20:49
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteau 7
La formule est bonne Scarta mais sans LaTeX c'est "un peu" ( euphémisme ) difficile à suivre 
Vasimolo
#5 - 27-02-2014 18:27:43
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#6 - 27-02-2014 21:16:52
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Gâtea u73
Soient A, D et D’ les diamètres respectifs du récipient, de la petite boule et de la grande boule.
Et soient E le volume d’eau versé (1 litre) et C la racine cubique de 2.
On a: 2.(1/6).pi.D³ = (1/6).pi.D’³ => D’ = D.C
De plus: E = pi.A².D - (1/6).pi.D³ = pi.A².D.C - 2.(1/6).pi.D³ => D = A.V[6.(C-1)]/2
=> E = A³.(pi/4).(2-C).V[6.(C-1)] => A³ = E/{(pi/4).(2-C).V[6.(C-1)]}
Au final, je trouve: A = 14.019157 cm, validé par la case-réponse.
Mais curieusement, en contradiction avec le post de Vasimolo qui précède, je trouve une densité de chocolat d'environ 0,74 < 1. Les boules ne devraient-elles alors pas flotter ? Ou ne devrait-on pas plutôt doubler leur poids (à chacune) ?
#7 - 27-02-2014 21:19:37
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
gâtezu 73
Je vais enfin avoir la réponse à un problème qu'on m'a posé il y a déjà quelque temps mais dont je n'ai aucune idée de la résolution, et oui la physique très peu pour moi, je vais attendre encore 61h donc 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#8 - 27-02-2014 21:26:26
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteeau 73
Tu as raison Franky , les chocolats de mon pâtissier doivent être en béton 
Vasimolo
#9 - 28-02-2014 18:42:10
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâteauu 73
@Shadock : ce n'est que des maths 
Vasimolo
#10 - 01-03-2014 12:19:58
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Gâteau 733
14.019157.
ça fait 2 jours que je l'ai, mais j'avais une virgule au lieu du point....
#11 - 01-03-2014 12:38:59
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1823
Gâetau 73
Il aurait pu pleuvoir, con comme il est ! (Coluche)
#12 - 01-03-2014 15:48:40
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
GGâteau 73
Bon je sèche pour le moment ! 
Je trouve r2=cuberoot(2)*r1 (rayons des 2 boules)
puis : R^2=125/(cuberoot(2)*pi*r1) + (2^(2/3)*r1^2)/6
On a aussi (en cm3) : 1000/8pi = r1*R^2 - r1^3/6 = r2*R^2 - r2^3/6
Je trouve finalement :
R^2=250/(pi*cuberoot(2)*sqrt(3*(cuberoot(2)-1))*(cuberoot(2)-1))
soit : 22.069... qui ne valide pas...
Je rentre mon bois et je reviens 
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#13 - 01-03-2014 16:17:06
- fmifmi
- Passionné de Prise2Tete
- Enigmes résolues : 18
- Messages : 87
Gâteau 733
Bonjour j'en avais assez de ces calculs de bourrin alors j'ai fait un algorithme qui me donne le résultat par itérations successives .
14,0191571298
pas très élégant mais çà marche
par contre , a propos du pâtissier, il faudrait lui dire que
ses boules flottent  je voulais dire les boules je voulais dire les boules
702 cm3 pour 520 grammes il n'y a pas de doute.
#14 - 01-03-2014 16:34:51
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Gâtau 73
Un petit bilan :
@Nodgim : c'est bon , j'avais précisé exprès la forme attendue 
@NickoGecko : oui mon pâtissier est un menteur , il veut naïvement nous faire croire qu'il utilise du chocolat . Il a tout de même eu la délicatesse de donner la masse de chocolat correspondant à ses boules .
@Fmifmi : ce n'est pas si bourrin que ça mais c'est vrai qu'il faut un peu d'application .
Bon courage à ceux qui cherchent encore .
Vasimolo
#15 - 01-03-2014 19:56:30
- fix33
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1198
- Lieu: Devant un clavier depuis 1748
Gâteeau 73
Je tombe sur une impossibilité : r1^2 = 6(cuberoot(2)-1)*R^2
donc r2>r1>R...
Je ne vien sur se site que pour faire croir que je suis treise intélligens.
#16 - 01-03-2014 21:00:44
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
GGâteau 73
Si Fix , c'est possible 
Vasimolo
#17 - 02-03-2014 11:06:34
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3615
- Lieu: 94110
Gâteau 7
Non, je n'ai pas testé le résultat avec 7 chiffres derrière la virgule, seulement avec les 6 que j'avais mis en gras.
Mais j'avais, comme nodgim, laissé une virgule à la place du point   ! !
#18 - 02-03-2014 12:45:46
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#19 - 02-03-2014 12:56:46
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Gâtteau 73
Seul le rapport (de 2) entre les masses des boules de chocolat sert à la résolution, mais pas les masses en elles-mêmes. Ton pâtissier peut donc les ajuster à sa guise.
#20 - 02-03-2014 14:02:00
- NickoGecko
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1823
Gâetau 73
Hello
Pour que les boules de chocolat aux masses données dans l'énoncé ne flottent pas, il faudrait que la densité du liquide leur soit inférieure (ou égale)
Pour 0.75, le pâtissier pourrait utiliser le rhum qu'il réserve à ses babas ?
(ou de l'essence ? de l'acétone ?)


Il aurait pu pleuvoir, con comme il est ! (Coluche)
|
 |

 Accueil
Accueil
 Forum
Forum