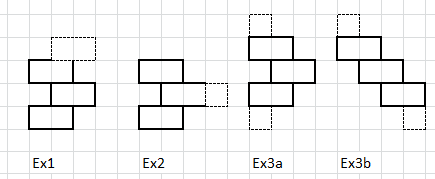Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 24-08-2010 00:36:22
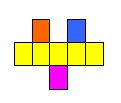
Ecchecs 5J'ai parlé il y a quelque temps des petites tours qui se déplacent sur les échiquiers comme leurs grandes soeurs mais d'une seule case à la fois
#0 Pub#2 - 26-08-2010 07:31:02
Ehecs 5Il n'y a pas beaucoup de réponses, je ne dois pas être le seul à patauger dans des démonstrations un peu fumeuses... mais bon, j'amorce la pompe pour faire réagir Vasimolo et récupérer un p'tit indice... #3 - 26-08-2010 12:37:21#4 - 27-08-2010 09:45:23
EEchecs 5Je propose une démonstration par récurrence. The proof of the pudding is in the eating. #5 - 28-08-2010 01:16:11#6 - 28-08-2010 01:37:07#7 - 28-08-2010 12:26:26
echecq 5Je ne suis convaincu par aucune des explications ci-dessus mais c'est parfois un peu difficile à lire et j'ai pu passer à côté de bonnes idées . #8 - 28-08-2010 15:38:40#9 - 28-08-2010 17:44:28#10 - 28-08-2010 18:04:45
ecjecs 5Merci car pour moi un domino est fait de 2 cases, comme pour ton énigme avec les points à jouer alternativement. Dans le cadre de la quinzaine du beau langage, ne disez pas disez, disez dites. (Julos Beaucarne) Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | |||||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.