Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil
Forum
|
 |
#1 - 02-09-2010 21:57:50
Trop ed zeros...Bonsoir,
#0 Pub#2 - 02-09-2010 22:19:17#3 - 02-09-2010 23:10:03
trop fe zeros...Bonsoir, On peut aussi écrire : 2010!=5∗10∗15∗...∗2005∗2010∗N (avec N premier avec 5) D'où 2010! = 5^4^0^2 * 1 * 2 * 3 * ... * 401 * 402 * N On peut aussi écrire : 2010! = 5^4^0^2 * 5 * 10 * ... * 400 * N' (avec N' premier avec 5) On continue à isoler les puissances de 5 : 2010! = 5^4^0^2 * 5^8^0 * 1 * 2 * ... * 80 * N' De fil en aiguille : 2010! = 5^4^0^2 * 5^8^0 * 5^1^6 * 5^3 * N'' (avec N"" premier avec N) 2010! = 5^5^0^1 * N"" Ces 501 puissances de 5, multipliées par leur équivalent en puissance de 2 généreront 501 zéros. Hommage : 
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit. #4 - 03-09-2010 07:48:22
trop se zeros...
The proof of the pudding is in the eating. #5 - 03-09-2010 08:01:18
Trop e zeros...
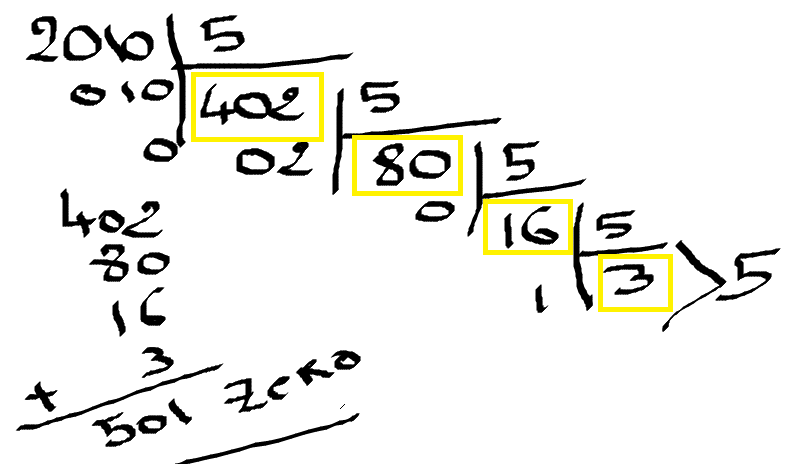
GETA -> traduction en français : La somme des entiers de la division de 2010 par 5 et ses puissances. Le temps est sage, il révèle tout. (Θαλής) #6 - 03-09-2010 09:33:38#7 - 03-09-2010 11:05:29
trop dr zeros...2010!=k×10n Et le nombre n est la réponse. En remarquant que 10 est le produit de 2 et 5 (niveau Terminale S au bas mot), il "suffit" de savoir combien de facteurs 2 et 5 sont impliqués dans le produit des nombres de 1 à 2010. A vue de nez, le facteur 2 sera immensément plus commun que le facteur 5 : vu qu'un nombre sur 2 est pair (niveau MPSI), ça nous fait plus de 1005 fois le facteur 2. Le facteur 5 apparaît une fois tous les 5 nombres, une fois de plus tous les 25 nombres, une fois de plus tous les 125 nombres, et une fois en plus en plus tous les 625 nombres (niveau Bac+5 en maths appliquées). Ca nous fait : - 402 nombres divisibles par 5 - plus 80 nombres divisibles par 25 (qui font partie des 402 précédents) - plus 16 nombres divisibles par 125 (même remarque) - plus 3 nombres divisibles par 625 (encore la même remarque) Soit 501 apparitions uniques du facteur 5 dans le calcul de 2010! (en sommant les nombres précédents, niveau Doctorat en sciences fondamentales). Le facteur 2 apparaissant largement plus souvent, l'écriture décimale de 2010! se termine par 501 occurrences du chiffre zéro. Je sèche sur la question subsidiaire (qui doit pourtant tenir de la recherche Google niveau CE1). En cherchant un peu, j'ai trouvé un des plus grands amateurs de mathématiques récréatives, Martin Gardner, mort en mai de cette année, et un article écrit en son hommage par... Normand Baillargeon. Oh tiens. Le monde est petit. Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #8 - 03-09-2010 11:40:07
Trop d zeros...Bonne réponse de tous. #9 - 03-09-2010 11:42:00
Trop dde zeros...Ce n'est pas de l'ironie quant à la difficulté du problème (avec lequel je me suis régalé), juste de l'auto-foutage de gueule sur ma façon de présenter sérieusement et avec détails un truc que tout le monde sait faire, qui a dégénéré en gros délire tout seul Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #10 - 04-09-2010 12:16:14
Trpo de zeros...1) "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #11 - 04-09-2010 12:32:52
Trop de zerso...Je suis un fan de Martin Gardner, décédé au début de cette année. Celui qui fuit les casse-tête ne vaut pas un clou. #12 - 04-09-2010 13:55:31#13 - 05-09-2010 22:53:30
Trop de zeors...Je viens de faire un peu de recherche pour dénicher le Haha en question et... The proof of the pudding is in the eating. #14 - 06-09-2010 00:07:43
Trop de zerros...Félicitations à tous ceux qui ont trouvé et aussi à ceux qui ont cherché. Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | ||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | ||||||||||||||||||||||||||||||||
Loin de moi l'idée de critiquer !
superficialité de société Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.
