 |
#1 - 04-12-2012 10:12:18
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
ptoblème de spirales
Ce problème est tiré de 100 friandises mathématiques de Ferachoglou et Lafond.
J'ai trouvé la solution particulièrement astucieuse alors je vous mets le problème (légèrement adapté).
Lors d'un concours de maths, les deux finalistes Titoufred et Vasimolo se retrouvent dans un grand gymnase. On leur pose une redoutable question de probabilité.
Lorsqu'ils réfléchissent, ils ont tous les deux tendance à faire une spirale en marchant.
Titoufred effectue 1 m au nord, 1 m à l'ouest, 2 m au sud, 2 m à l'est, 3 m au nord ...
Vasimolo effectue 1 m à l'ouest, 1 m au sud, 2 m à l'est, 2 m au nord, 3 m à l'ouest.
Il commence à réfléchir (et donc à marcher) en même temps à midi. Ils marchent tous les deux à 1m/s.
Au départ Vasimolo est 27 m au sud et 17 m à l'est de Titoufred.
A quelle heure vont-ils se rencontrer?
#2 - 04-12-2012 14:04:24
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Problème de spiralees
Voici la distance de Titoufred à Vasimolo (vers le Sud ; vers l'Est) suite aux 8 premiers mouvements :
(27;17) => (28;16) (29;17) (27;19) (25;17) => (28;14) (31;17) (27;21) (23;17)
J'ai regroupé les mouvements par séquences de 4, séparés par des =>, et représenté les séquences 1 et 2.
On peut facilement montrer par récurrence que la séquence n est la suivante :
(29-2n ; 17) => (28 ; 18-2n) (27+2n ; 17) (27 ; 17+2n) (27-2n ; 17)
Pour que les personnages puissent se rencontrer, il faut que les deux coordonnées changent de signe entre 2 mouvements. Ce qui ne peut être le cas que sur le premier mouvement d'une séquence n, lorsque l'on passe de (29-2n ; 17) à (28 ; 18-2n).
Si l'on note t le temps (en secondes) écoulé depuis le début cette séquence n, la position relative est (29-2n+t ; 17-t).
Il faut donc 29-2n+t = 0 et 17-t = 0 ce qui donne t = 17 et n = 23.
Il ne reste plus qu'à calculer le temps écoulé depuis le début :
1+1+2+2+3+3+...+43+43+44+44+17=44*45+17=1997 secondes
J'aurai donc le plaisir de rencontrer Vasimolo à 12h33m17s !
#3 - 04-12-2012 14:26:58
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
Problèème de spirales
Bonjour,
Je trouve la rencontre à 12h 33m 17s.
Mais mon raisonnement n'a rien de très astucieux. 
Je choisis un repère orthonormé dans le plan, avec l'axe des x orienté d'Ouest vers l'Est et l'axe des y orienté du Sud vers le Nord, puis je cherche la position de Titoufred dans le repère de Vasimolo.
Dans le repère de Vasimolo, Titoufred recule de 2 mètres vers le Sud au bout d'un cycle de spirale.
Au bout de 22 cycles, Titoufred aura donc reculé de 44 mètres vers le Sud par rapport à Vasimolo. Puis 17 secondes plus tard, il sera remonté de 17 mètres vers le Nord et de 17 mètres vers l'Est, toujours par rapport à Vasimolo. Il sera donc 27 m plus au Sud et 17 m plus à l'Est, ce qui correspond à leur éloignement initial.
Donc ils sont l'un sur l'autre ! 
Il reste à calculer le temps nécessaire aux 22 cycles :
1+1+2+2+3+3+...+43+43+44+44 = 1980 secondes
Temps total = 1980+17 = 1997 secondes.
La rencontre a lieu à midi + 1997 secondes, soit à 12h 33m 17s.
J'espère que je ne me suis pas trompé et j'attends maintenant la solution astucieuse...
Klim.
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#4 - 04-12-2012 15:04:45
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
problème de spiralzs
Après un joli schéma simplifié sur papier
j'arrive à 7939 secondes avant la rencontre, soit 14h12m19sec
mais j'ai du me planter quelque part. 
#5 - 04-12-2012 15:15:50
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
Problème de spiraless
Ok pour titoufred à l'heure au rendez-vous, ainsi que pour klim.
@nobodydy: une erreur en effet
Le format de la réponse est: xxhxxmnxxs
#6 - 04-12-2012 16:09:47
- nobodydy
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1677
#7 - 04-12-2012 16:16:18
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
Probème de spirales
C'est bien ça. Un problème de format de réponse sans doute.
#8 - 04-12-2012 16:23:54
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
pronlème de spirales
12H33MN17S
Je me suis torturé le cerveau et j'ai vraiment été surpris de ne pas avoir fais d'erreur pour trouver la réponse.
Voici mon graphique pour trouver la solution.
C'est un peu confus donc j'attendrais la solution claire et concise, en attendant je me suis bien amusé à chercher.
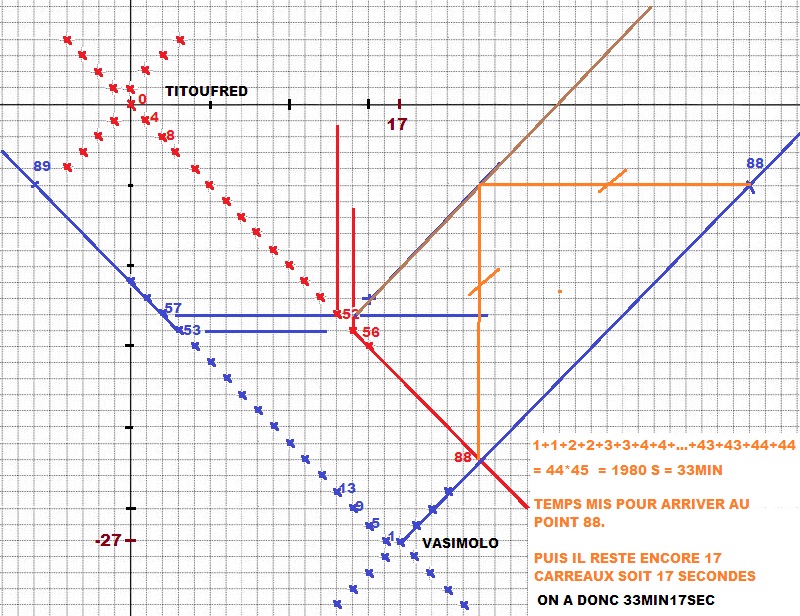
http://www.prise2tete.fr/upload/gilles355-SPIRALES.jpg
#9 - 04-12-2012 16:41:40
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
Problème de spirles
Plusieurs façons de faire, même si celle de Gilles me laisse perplexe  . .
#10 - 04-12-2012 17:54:14
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Problème de spiralees
Pour me simplifier la vie, au lieu de chercher le point d’intersection entre les 2 spirales de Titoufred et de Vasimolo, je fabrique une troisième spirale qui part du point origine et qui est la différence entre les deux précédentes, puis je regarde quand cette spirale rencontre le point d’abscisse x0=17 et d’ordonnée y0=-27. Cette spirale fera respecti- vement V2 m au nord-est, V2 m au nord-ouest, 2V2 m au sud-ouest, 2V2 m au sud-est, 3V2 m au nord-est, etc… Je m’intéresse au quart sud-est, là où se trouve le point indiqué.
Le temps écoulé à l’intersection de chacun des segments de droite de ce quart sud-est (de rang n) avec l’axe des ordonnées sera de: (2n+1)²- (2n+1) = 2n.(2n+1), et avec l’axe des abscisses de: (2n+1)² - 1 = 4n.(n+1). Chaque segment de droite de ce quart sud-est a pour équation: y = x - 2n.
Cherchons maintenant n à l’intersection avec le point indiqué: n = (x0–y0)/2 = 22, correspondant au segment de rang 22, avec des temps écoulés au niveau de l’axe des ordonnées de: 2n.(2n+1) = 1980, et de l’axe des abscisses de: 4n.(n+1) = 2024.
Le temps écoulé cherché est donc de: 1980 + 17 = 1997, ou: 2024 - 27 = 1997.
Après un parcours de 1997 secondes, il sera : 12 h 33 mn 17 s, validé par la case-réponse : ouf !!!
#11 - 04-12-2012 18:16:15
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
Probème de spirales
D'ailleurs avec ma méthode, à expliciter je sais, je peux aussi prévoir le lieu de leur rencontre !
En effet ils se rencontreront en faisant leur 23ème tour à :
5m au sud et 22m à l'est de Titoufred ou ecore à :
22m au nord et 5m à l'est de Vasimolo.
Tiens ? 22+5=27 et 22-5=17 ...
#12 - 04-12-2012 18:59:20
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
#13 - 04-12-2012 20:29:36
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
problème de spieales
Je trouve 12h33mn17s, après avoir dessiné une partie du trajet et dessiné l'endroit de la rencontre... Mais ça n'était pas très formalisé !
#14 - 04-12-2012 20:49:31
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,194E+3
#15 - 04-12-2012 22:13:45
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
Problèème de spirales
@vasimolo: le choix des armes ne m'appartient pas
@golgot: ok
@gwen: non, le format de vérification est xxhxxmnxxs
#16 - 04-12-2012 22:28:50
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
problème de spitales
@racine: Suis-je mis hors course ? J'en ai pourtant bavé pour ma démo (je n'ai pas mis les calculs détaillés).
#17 - 04-12-2012 22:50:09
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
problème dr spirales
Racine , tu n'es que l'arbitre 
Chez les mathématiciens il existe une très longue tradition de joutes et défis souvent amicaux mais parfois virulents . J'aime bien quand il y a du challenge mais j'aime aussi prendre mon temps et je n'en ai pas beaucoup en ce moment .
Vasimolo
#18 - 04-12-2012 23:09:07
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
pronlème de spirales
@franky: le résultat est bon, je croyais que tu l'avais validé. Pour la démo il fait que de regarde ailleurs que sur mon téléphone (et encore mon expertise ne vaut pas grand chose). Mais pour info, la démo astucieuse passe justement par le point d'intersection.
#19 - 04-12-2012 23:15:20
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
ptoblème de spirales
@racine: Ma démo est effectivement assez lourde (quoique probablement juste). Mais je n'ai pas trouvé l'astuce qui donne le résultat en quelques lignes (ce que Martin Gardner appelle le "haha").
#20 - 04-12-2012 23:35:39
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
Problème de spirale
Quand tu parles d'intersections est_ce des droites y1=17-x et y2=x-27 ?
Car moi l'intersection de ces deux droites me donnent justement leur point de rencontre en supposant que titoufred est à l'origine du repère et Vasimolo à (17;-27).
#21 - 04-12-2012 23:42:23
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
problème de spirakes
@gilles: oui, ça doit correspondre. Mais l'argument qui permet de trouver le point d'intersection est dans une base de réflexion totalement différente.
#22 - 05-12-2012 19:06:39
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Problèm ede spirales
Ce que je peux dire, c'est que la rencontre se fera, si T est de coordonnées (0,27) et V(17,0) sur un point de la droite x=y.
#23 - 07-12-2012 09:05:21
- racine
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1224
Prolbème de spirales
La feinte est la suivante.
Les deux spirales sont images l'une de l'autre par une rotation de centre O et de 90°.
Le point de rencontre est donc le seul point égal à sa propre image, donc O.
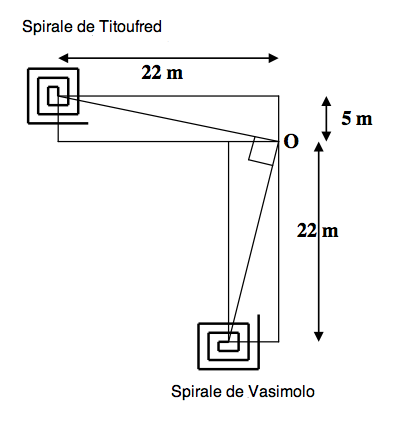
Après, yapuka:
Au bout de 22 tours Titou aura fait 22 m à l'est et 22 m au sud. Il sera donc 17 m au sud de O.
22 tours= 1+1+2+2+3+3...+44+44= 45*44=1980m
On remonte de 17 m
Et on obtient 1997 m , soit autant de secondes.
Donc la rencontre a lieu à : 12h33mn17s
#24 - 07-12-2012 11:35:29
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
#25 - 07-12-2012 14:19:48
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
prpblème de spirales
Ohhhh
très joli en effet !
Bravo !
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum









