Pour une, deux et quatre feuilles, il n'y a eu finalement que des bonnes réponses. Je me contente juste de résumer les résultats, pour le cas général, avec un coté de feuille [latex]c[/latex].
[TeX]
\fbox{
r_1=c/2
r_2=c(2-\sqrt 2)
r_4=c
}
[/TeX]
Bon, le cas à quatre feuilles, était juste là pour voir si après avoir été conditionné par les cas précédents, vous alliez y passer plus de dix minutes... Il n'y a que vous qui pouvez le savoir... 
Pour trois feuilles, j'ai bien peur que seul McFlambi ait trouvé la solution (sous une forme un peu particulière quand même! 
). Bravo à lui.
Voici ma configuration (zoom possible):
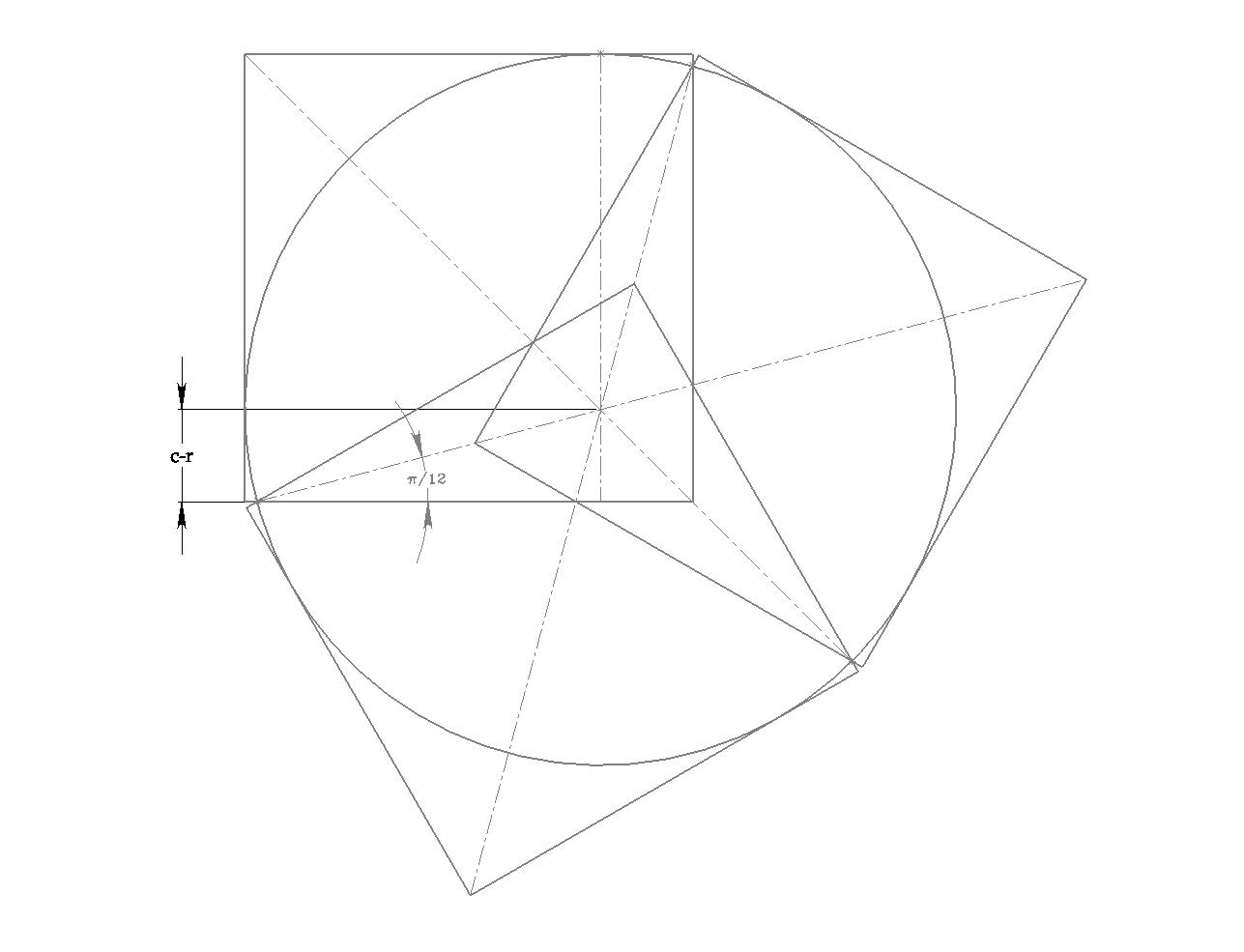
On a directement:
[TeX]
\sin \frac{\pi}{12} = \frac{c-r_3}{r_3}
[/TeX]
En utilisant l'identité remarquable portant sur le cosinus d'une somme, on tire la valeur de [latex]\sin\frac\pi{12}[/latex] et il vient:
[TeX]\fbox{r_3=\frac{2c}{2+\sqrt{2-\sqrt{3}}}[/TeX]
Merci à tous pour votre participation.
NB1: Je ne sais pas démontrer que mes configurations sont optimales, si vous voyez comment faire, n'hésitez pas à le dire.
NB2: Si ça vous a plu, il y a actuellement un autre problème du même goût (plus dur il me semble) ici.
Accueil
)
