|
#1 - 14-10-2010 23:21:32
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
recouvrement d'une pmaque carré.
Je dispose cette fois de quatre disques de carton de rayon 1.
Quel est le coté de la plus grande surface carré que l'on peut recouvrir avec un, deux, trois, puis quatre disques.
Merci de donner des valeurs exactes.
Bon courage.
#2 - 15-10-2010 00:37:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Recouvrement d'une plque carré.
Un peu de patience , le problème inverse n'est toujours pas résolu 
Vasimolo
#3 - 15-10-2010 18:20:43
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
recouvrement d'une plasue carré.
pour 1 carré, c'est le carré inscrit et donc [latex]c=\cos(\pi/4)=1/\sqrt2\approx0.71[/latex],
pour 4, j'ai deux idées, une qui consiste a faire le plus symétrique possible, ce qui donne 4 cercles en formation carrée et comme la diagonale fait 4, le coté fait [latex]2\sqrt2\approx2.83[/latex], sinon je les verrais en rosace formation losange mais je pense que c'est moins bon.
pour 2, je vois deux cercles alignés (centres A et B) et un carré, tous à l'horizontale (les cotés du carré étant verticaux et horizontaux), comme sur la figure ou on a un rectangle qui selon [latex]\alpha[/latex], passe par rectangle tout écrasé pour [latex]\alpha =0[/latex] ou un rectangle tout en hauteur pour [latex]\alpha=\pi/2[/latex]

Les longueurs des cotés du rectangle sont :
[TeX]4\cos\alpha[/latex] et [latex]2\sin\alpha[/TeX]
En postulant que c'est optimal quand le rectangle est un carré, càd pour
[TeX]4\cos\alpha=2\sin\alpha[/latex] ou [latex]\tan\alpha=2[/TeX]
et
[TeX]c=2\sin\alpha=2\sin(\arctan(2))[/TeX]
ce qui donne avec Thalès [latex]\frac1{\sqrt{1^2+2^2}}=\frac{\cos\alpha}{\tan\alpha}=\sin\alpha[/latex]
donc [latex]c= \frac2{\sqrt5}\approx0.89[/latex]
pour le 3 je verrais demain... la dodo
#4 - 15-10-2010 19:11:44
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
Recouvrmeent d'une plaque carré.
McFlambi, pour le raisonnement, je suis d'accord, mais il y a une erreur de calcul pour un et deux disques (de rayon 1...).
Bonne nuit. 
#5 - 15-10-2010 19:20:07
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Recouvrement d'unee plaque carré.
Pour un disque le côté du carré est [latex]\sqrt{2}[/latex] et pour deux [latex]\frac{4}{\sqrt{5}}[/latex] 
Les figures vont suivre .
Vasimolo
#6 - 15-10-2010 20:01:02
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
rexouvrement d'une plaque carré.
Vasimolo, pour l'instant, je suis d'accord. Bonne continuation. 
#7 - 15-10-2010 20:21:11
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Recouvrement d'une plaque carré
J'avais donné le demi-côté 
J'ai corrigé 
Vasimolo
#8 - 16-10-2010 07:55:44
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
Recouvrement d'une pplaque carré.
ah oui c'est 2 fois plus pour les deux je crois....
#9 - 16-10-2010 11:33:04
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Recouvrement du'ne plaque carré.
Pour quatre disques un carré de côté [latex]2\sqrt{2}[/latex] , trois à suivre :

Vasimolo
#10 - 16-10-2010 11:39:51
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
recouvtement d'une plaque carré.
Un seul disque de rayon 1 recouvre un carre d'aire 2 et donc de cote [latex]sqrt2=1.41[/latex]
deux disques recouvrent un carre de cote [latex]\frac{4sqrt5}{5}=1.78[/latex]
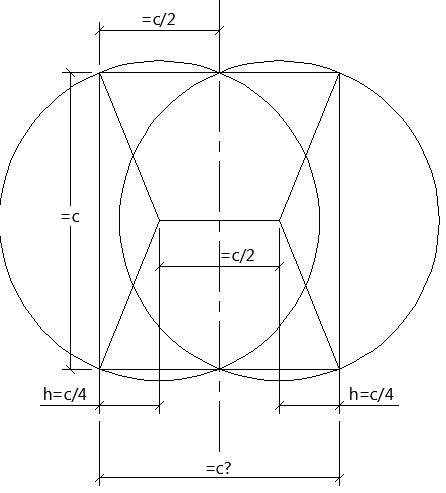
Les disques sont de part est d'autre de l'axe de symetrie. La hauteur du triangle de cote, r, r et c doit être egale à c/4 ce qui donne
[TeX]\Delta=d(C_1,C_2)=c/2~ \Longrightarrow ~c/4 = sqrt{1-c^2/4}[/TeX]
avec trois disques,
c=presque 2!
Je cherche une symetrie de centre O, avec rotation de 120 deg.
soit x la distance C1 à O
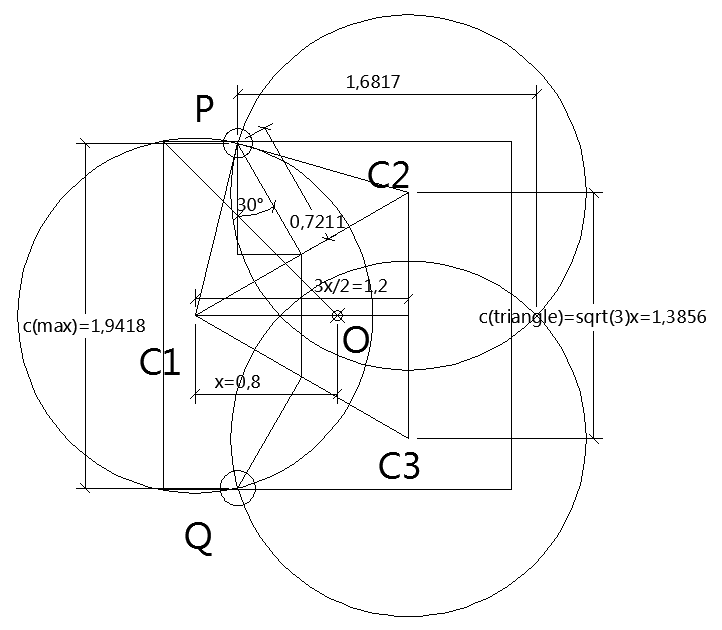
condition 1: distance verticale
demi-cote du triangle reliant C1,C2 et C3
+2 verticales de la hauteur de C1,P,C2
ce qui donne
[TeX]C_{1max}=\frac{sqrt3}{2}\time (sqrt{4-3x^2}+x)[/TeX]
max at [latex]1/sqrt3[/latex]
mais coince avec condition 2: distance horizontale
...
j'abandonne, pas le temps
avec 4 disques, le centre de symetrie se trouve sur le cercle et donne une jolie rosace. La diagonale du carre inscrit mesure 2 diametres donc 4 ce qui implique un cote de [latex]2\sqrt2[/latex]
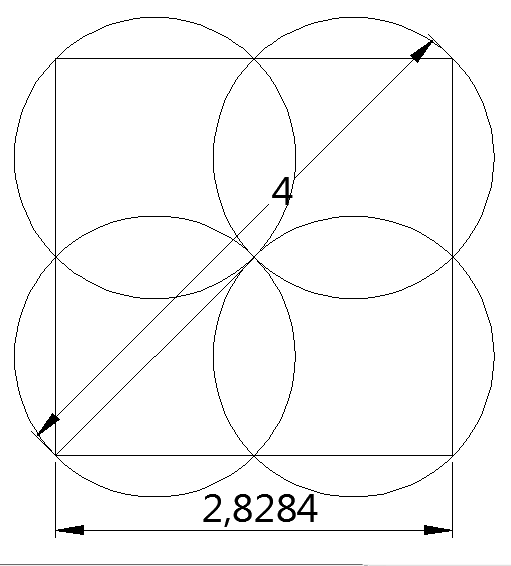
The proof of the pudding is in the eating.
#11 - 16-10-2010 12:08:47
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
Recouvrment d'une plaque carré.
Franck, Bravo pour un, deux et quatre disques.
Pour trois tu y es presque. Ta figure ne décrit pas une configuration unique, elle dépend de la distance entre deux centres de disque par exemple. Ma configuration est la tienne en minimisant cette distance...
Bon courage. 
#12 - 17-10-2010 17:48:05
- Yannek
- Passionné de Prise2Tete
- Enigmes résolues : 10
- Messages : 60
recouvremeny d'une plaque carré.
Je pense que les solutions sont :
* [latex]\sqrt 2[/latex] (facile, sans commentaire)
* [latex]\frac {4\sqrt 5}5[/latex] moins facile, je poste une démo
* [latex]\frac {\sqrt2+\sqrt 6}2[/latex] je vois la configuration, mais ne sais pas encore prouver qu'elle est optimale
* [latex]2\sqrt{2}[/latex] plus facile à prouver que la configuration précédente, mais je n'y ai pas encore réfléchi
Démo du cas 2 disques :
* Soient O et O' les centres des deux cercles, d la distance entre ces deux centres, M le milieu de [OO'] et A,B les points d'intersection des deux cercles (on suppose assez clairement d<2).
Soit un carré EFGH de côté c maximal contenu dans l'union des deux disques et C sont centre.
* On peut supposer que C=M :
Le symétrique du carré par rapport à O est également contenu dans l'union des deux disques (qui a O pour centre de symétrie).
On suppose que les deux carrés se coupent (c'est la cas si l'on ne peut inscrire le carré initial dans un seul disque). Alors M appartient aux deux carrés, et plus généralement l'image par la translation de vecteur CM du carré initial est contenue dans les deux disques. (par convexité et symétrie de l'union des surfaces des deux carrés)
* [latex]c\leq 2\sqrt{1-\left(\frac d2\right)^2}[/latex]
En effet, O étant le centre du cercle et c la plus petite distance entre deux points de deux segments opposés du carré, c est inférieur ou égal à AB. On montre (Pythagore) que MN est le second membre de l'équation ci-dessus.
* [latex]c\leq 2d[/latex]
Soient P et Q les intersections (en dehors de A) de la perpendiculaire à (AB) qui passe par A avec les deux cercles. On montre (Thalès) que PQ=2d et de même que pour le point précédent, c doit être inférieur à 2d.
* [latex]d=\frac{2}{\sqrt 5}[/latex]
Pour optimiser c satisfaisant les deux inéquations précédentes on résoud
[TeX]2d=2\sqrt{1-\left(\frac d2\right)^2}[/TeX]
On trouve le résultat annoncé pour c, (et on valide l'hypothèse faite à la première étape du raisonnement).
Je suis certain qu'il existe des démos beaucoup plus élégantes de ce point (et je suis curieux de voir les preuves rigoureuses pour les deux autres situations...)
#13 - 17-10-2010 18:22:43
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
recouveement d'une plaque carré.
Yanneck, bravo pour un, deux et quatre disques. Pour trois disques, j'ai un peu mieux. Cependant, je ne peux sais pas démontrer que j'ai la meilleure configuration... Bonne continuation. 
#14 - 17-10-2010 19:19:19
- LeSingeMalicieux
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1298
- Lieu: Haute-Marne
Recouvrement d'une plaque acrré.
Avoir quatre mains, c'est plus pratique pour taper sur un clavier.
#15 - 17-10-2010 19:30:50
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
Recouvrement d'une paque carré.
LeSingeMalicieux, Bravo, tous les résultats me paraissent corrects. Pour trois disques, j'ai la même configuration ma configuration ressemble à la tienne, y a plus qu'à... Bon courage. 
#16 - 17-10-2010 20:31:43
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Recouvrement d'une plaque carrré.
Pour 1 disque : √2 = 1.414213562
Pour 2 disques : 2×√(4÷5) = 1.788854382
pour 3 disques: √3+(2×√2−√3)÷5 = 1.951326071
Pour 4 disques : 2×√2 = 2.828427125
pour 3 disques les centres des disques sont disposés en triangles équilatéral a une distance de 1 l'un de l'autre.
pour 4 disques les centres des disques sont disposés en triangles carré avec le bord des cercles se touchant au centre.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#17 - 17-10-2010 21:04:22
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
recouvrement d'une plaque catré.
dhrm, je suis d'accord pour un, deux et quatre, bravo. Pour trois, on peut faire mieux. Je suis d'accord avec la disposition des centres, moi je les ai plus espacé... Bonne continuation. 
#18 - 19-10-2010 11:40:54
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
recouvremeny d'une plaque carré.
Beaucoup de bonnes réponses pour un, deux et quatre disques, je résume donc:
[TeX]\fbox{
c_1=\sqrt 2 r
c_2=\frac{4}{\sqrt{5}} r
c_4=2\sqrt 2 r}
[/TeX]
Pour trois disques, je les place de telle façon à ce que leur centre soient aux sommets d'un triangle équilatéral. J'ajuste la distance entre deux centres pour caser la plaque carré comme ceci (zoom possible):
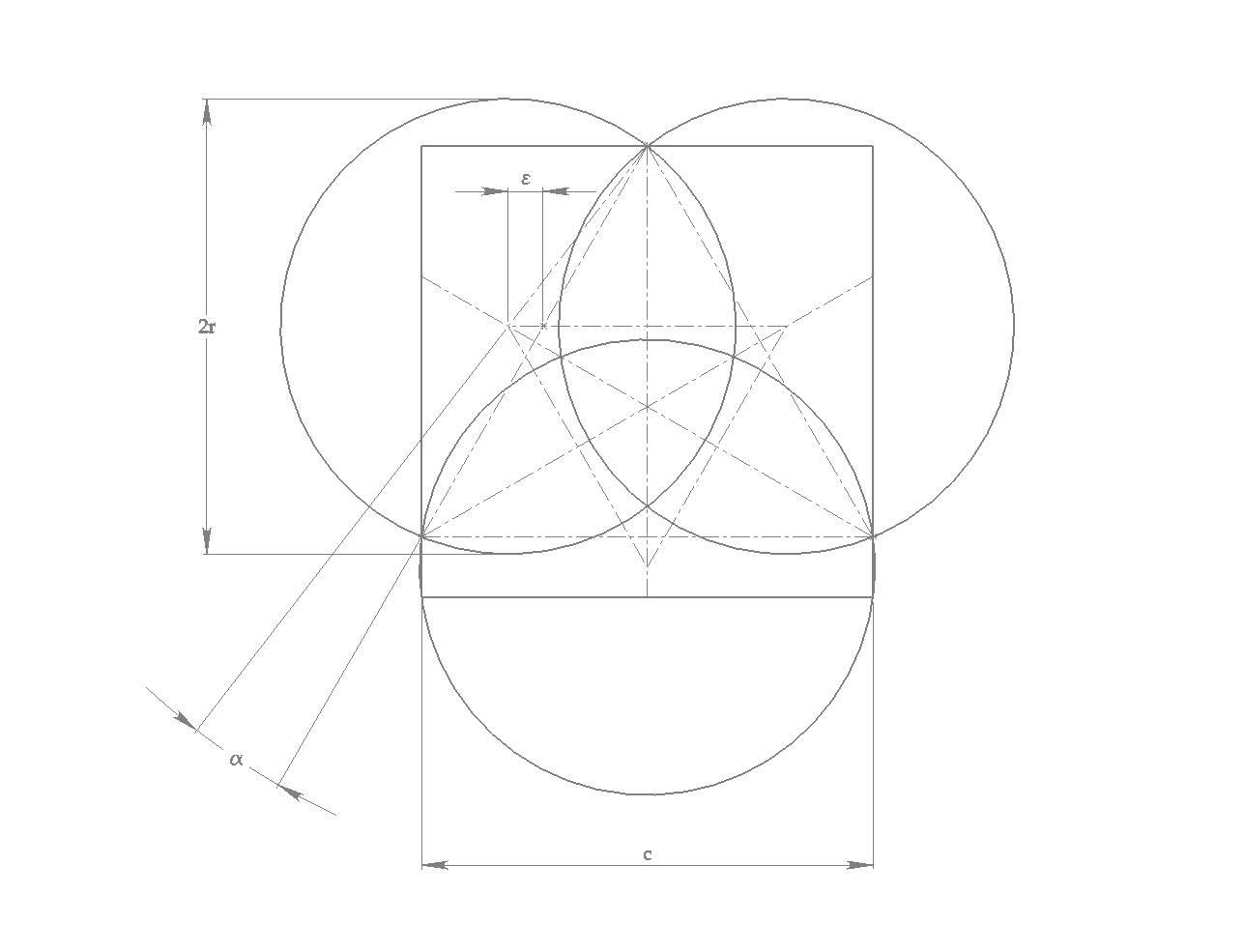
Je commence par montrer la relation:
[TeX]\varepsilon=\left(\frac{1}{\sqrt{3}}-\frac 1 2 \right)c_3 [/TeX]
Puis, je constate que:
[TeX]
\sin \alpha =\frac{\sqrt{3}\varepsilon}{2r}
\cos \alpha=\frac{c_3}{2r}
[/TeX]
Puis, en utilisant le fait que la somme des carrés de cosinus et de sinus fait un, il vient:
[TeX]\fbox{
c_3=\frac{2r}{\sqrt{\frac{11}{4}-\sqrt 3}}}[/TeX]
Merci pour votre participation.
#19 - 19-10-2010 13:33:55
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
Recouvrement dd'une plaque carré.
Luthin, apparement pour trois disques on peut faire legerement mieux.
Je trouve maintenant 1.98455575342734
A comparer a ce que tu trouves: 1.982288879
En rapprochant les 2 disques du haut on peut faire monter le carré un petit peu jusqu'a ce que les coins du carré en haut touchent aussi les 2 cercles du haut.
(voir le dessin du SingeMalicieux plus haut)
X repond a l'equation:
[TeX]2\sqrt{1-\frac{x^2}{4}} + 2\sqrt{1-\frac{x^2}{16}} = x[/TeX]
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#20 - 19-10-2010 16:55:31
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
Recouvrement 'dune plaque carré.
#21 - 20-10-2010 01:22:46
- dhrm77
- L'exilé
- Enigmes résolues : 49
- Messages : 3004
- Lieu: Fanning Island-?-Lac Tele,Mali
rrcouvrement d'une plaque carré.
Ca, ca s'appelle du travail en équipe. LeSingeMalicieux fait un dessin, je trouve son équation, et luthin la resoud...
Je dis ca parce que je ne savais pas résoudre cette équation, si j'ai le nombre c'est a cause de Calc (l'équivalent de Excel sur OpenOffice)
Et je confirme que c'est bien [latex]\frac{16}{\sqrt{65}}[/latex], merci luthin.
Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt
#22 - 20-10-2010 06:56:20
- franck9525
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1935
- Lieu: 86310
Recouvreement d'une plaque carré.
pas besoin d’être un génie en math avec ce site! 
http://www.wolframalpha.com/input/?i=2\ … 6}}+%3D+x
J'ai copie colle la formule latex directement. Ce site vient maintenant devant Wiki lors d'une recherche sur Google relative aux maths. J'en avais entendu parlé sur "de quoi je me mail" il y a probablement un an.
The proof of the pudding is in the eating.
#23 - 20-10-2010 08:29:38
- luthin
- Professionnel de Prise2Tete
- Enigmes résolues : 36
- Messages : 124
rrcouvrement d'une plaque carré.
J'ai cru au début qu'il fallait avoir recours à l'informatique pour résoudre cette équation... Il n'en est rien, il suffit d'élever deux fois au carré pour faire disparaitre les racines. Effectivement, inutile d'être un génie! 
#24 - 20-10-2010 14:47:47
- McFlambi
- Professionnel de Prise2Tete
- Enigmes résolues : 48
- Messages : 144
Recouvremetn d'une plaque carré.
Pour vous autres fans de figures et latex, je vous conseille Geogebra... On dessine vite, bien, precis et tout... Et on peut sortir des figures via latex (il exporte du code pour la figure direct en tikz, un package de latex, le "usepackage" etant deja integré... rien a faire donc) et vous pouvez ensuite avoir des figures en qualité vectorielle, ce qui n'est pas un luxe pour les figures "en grand"
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum