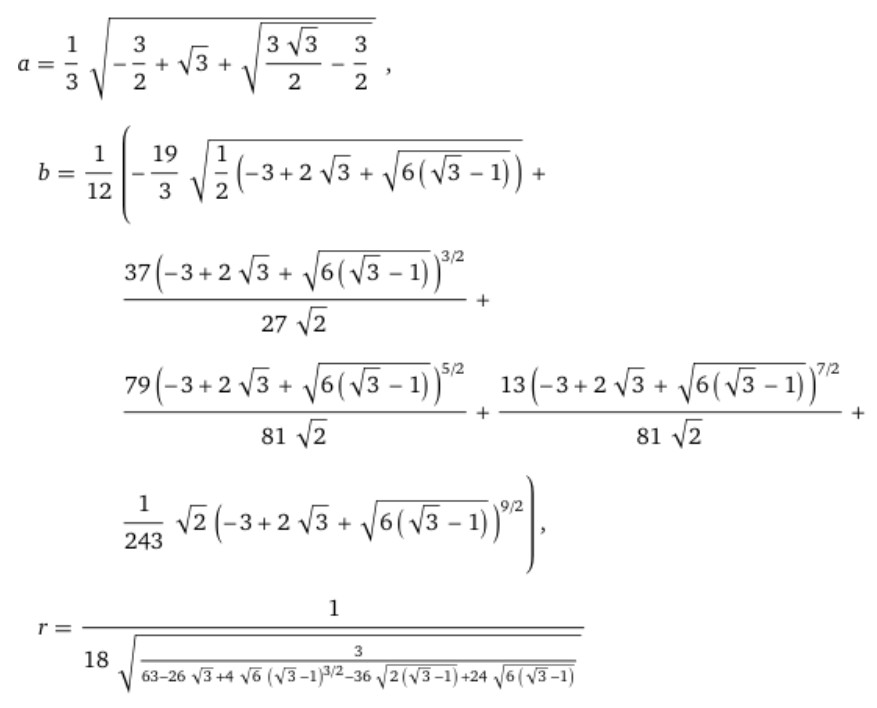Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 03-05-2025 17:06:12
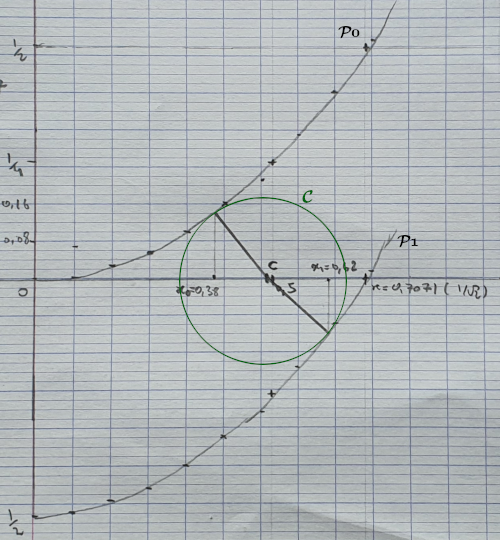
Cecrle tangent à 2 parabolesBonjour
#0 Pub#2 - 03-05-2025 17:45:15#3 - 03-05-2025 17:54:26
eCrcle tangent à 2 parabolesNon aunryz. En regardant sur un logiciel de géométrie dynamique la réponse est environ 0,178. J'aimerai avoir une valeur exacte #4 - 08-05-2025 01:52:10
Cercle tangent à 2 parabolsSalut Gabriel, #5 - 08-05-2025 16:36:21
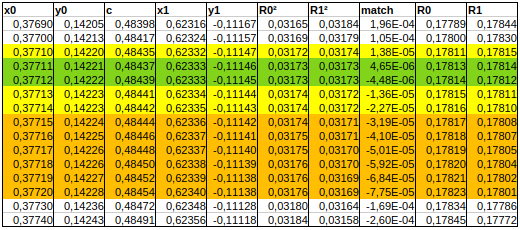
cercle rangent à 2 parabolesBonjour à tous, aujourd'hui, recherchons une solution approchée #6 - 11-05-2025 10:23:32
cercle tangent à 2 parabolzsEn prenant a , l'abscisse du premier point de tangence pour y=x^2: #7 - 11-05-2025 14:41:53
cercle tanhent à 2 parabolesJ'avais cherché le problème sans aboutir à la solution, cependant je suis perplexe devant le sens de l’esthétique mathématique de wolfram. Je me suis amusé à simplifier et j'arrive à ça : #8 - 11-05-2025 18:08:18#9 - 11-05-2025 18:39:29
Cercle tangnet à 2 parabolesHello. J'avais également cherché sans aboutir, bloqué par des équations imbuvables. #10 - 18-05-2025 08:17:46
Cercle tngent à 2 parabolesMerci beaucoup moi j'avais une équation du 4eme degré avec la méthode de Ferrari a faire. Je vous enverrai lundi la solution que j'avais trouvé. #11 - 19-05-2025 17:14:07
Cercle tangent à 2 paarbolesCoucou voici ce que j'avais trouvé. Réponse rapideSujets similaires
|
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.