Soit O le centre du cercle.

Calcul des angles:

CA'B = 2*pi  - CAB
BA'C" = BCA/2
CA'B'  =ABC/2

CA'B = B'A'C' + ABC/2  +BCA/2

B'A'C' = 2*pi -  CAB -   ABC/2  -  BCA/2  =  pi   -   CAB/2 

B'OC' = â'   =  2* pi  - CAB
CAB  = â
la surface B'OC' est égale à S'= cosâ'   * sinâ'  = cos â    *  sin â qui définit la surface OCB
donc les deux surface sont égales. Par extension les deux triangles ont des surfaces égales

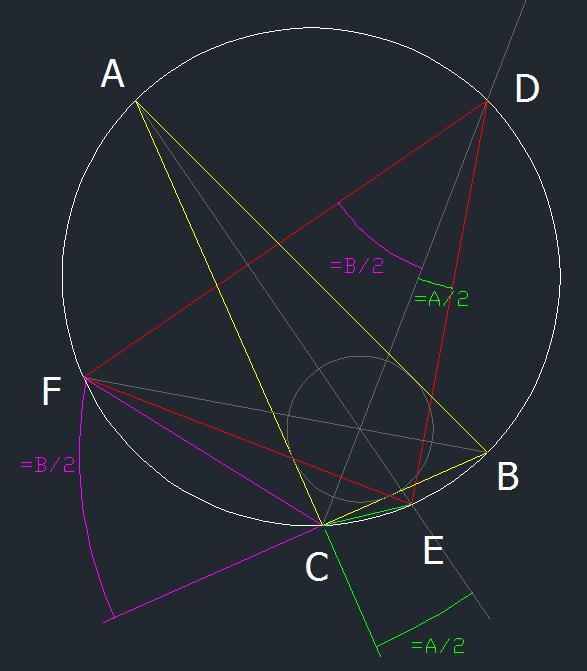
Soit le triangle jaune ABC. Les bissectrices (en gris) coupent le cercle circonscrit pour former le triangle rouge DEF.
La corde verte CE est commune aux angles CAE et CDE qui ont donc le même angle A/2.
La corde magenta CF est commune aux angles FDC et FBC.
L'angle du sommet D du triangle rouge est donc A/2+B/2.



L'aire d'un triangle peut être calculée à partir de ces trois angles et du diamètre du cercle circonscrit.
$$P=Aire_{ABC}=\frac{1}2\emptyset^2 sin(A) sin(B) sin(C)$$
ce qui nous donne
$${\frac{Q}P=\frac{sin(\frac{A+B}2) sin(\frac{A+C}2) sin(\frac{B+C}2)}{sin(A) sin(B) sin(C)}}$$
Puisque $A+B+C=\pi$, l'expression peut se simplifier
$${\frac{Q}P=\frac{1}{8cos(\frac{A+B}2)sin(\frac{A}2)sin(\frac{B}2)}$$

Si quelqu'un comprends quelque-chose, il est le bienvenu pour expliquer...

Je crois que tout le monde est d'accord...

Comme me le signaler Hallodulla, c'est plus joli de remettre C dans l'équation à la fin, ce qui donne :
$$5$ \red\fbox{\frac P Q=8sin(\frac{A}2)sin(\frac{B}2)sin(\frac C 2)}$$