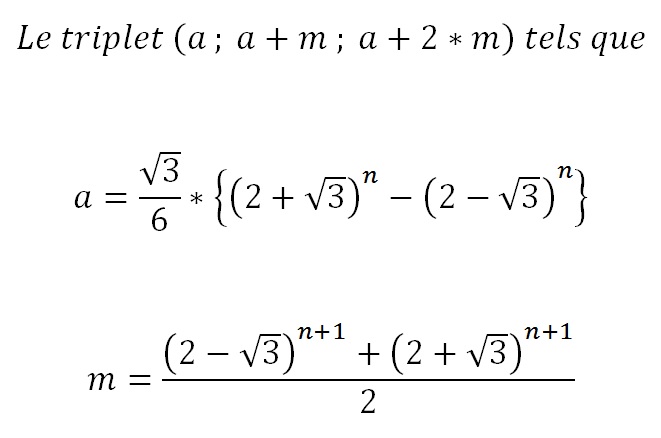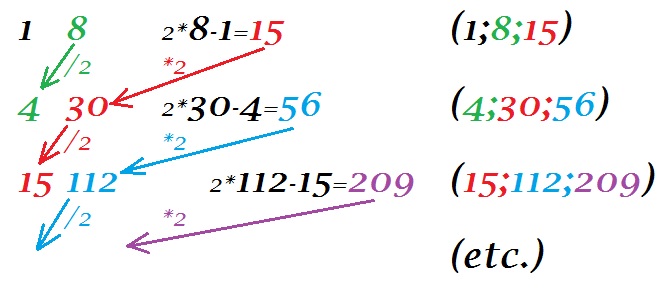|
#1 - 08-04-2015 18:41:22
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
produuts presque carrés (difficile)
Salut à tous,
Il y a 4 ans et demi, je vous avais parlé du PEN (comment ça vous vous rappelez pas ? Mais si, ici  ) )
J'aimerai vous présenter le second problème.
Trouver une infinité de triplets a, b et c tels que
- a, b, c soient en progression arithmétique
- ab+1, ac+1 et bc+1 soient tous les trois carrés
Il y a quatre ans, je me rappelle avoir trouvé une solution compliquée (très compliquée en fait, d'ailleurs je ne me rappelle plus de tout en détail). Mais dans un coin de ma tête, je me demandais si on ne pouvait pas trouver plus simple. Et c'est le cas, j'en ai enfin la preuve.
Donc trouvez une infinité de triplets qui vérifient les deux propriétés ci dessus 
Indice Spoiler : [Afficher le message] ayant déjà ab+1 carré, quel c vérifiera toujours ac+1 et bc+1 carrés ?
Indice 2 : Spoiler : [Afficher le message] c=a+b+2x marche toujours pour x égal une certaine valeur
Précision : je pense qu'il est simple de vérifier que la solution est la bonne bien qu'elle soit difficilement intuitable. Mais comme je le disais plus haut, elle reste simple donc c'est pas impossible : au cas où donc, je préfère préciser que c'est bien le cheminement qui m'intéresse et pas la solution en elle même.
#2 - 08-04-2015 19:11:23
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Produits persque carrés (Difficile)
Y'en a qui aiment , mais c'est sans moi 
Vasimolo
#3 - 08-04-2015 19:52:46
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Produits presqu ecarrés (Difficile)
Moi j'aime pas les biscuits 
#4 - 08-04-2015 21:13:00
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
produits presque carrés (diffixile)
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#5 - 08-04-2015 22:36:04
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
produits presque catrés (difficile)
Salut !
1,8,15 fonctionne...
1*8+1=3²
1*15+1=4²
8*15+1=11²
(Par bêtes essais successifs...)
Edit :
4; 30 et 56 aussi !
4*30+1=11²
4*56+1=15²
30*56+1=41²
(Même méthode !)
#6 - 08-04-2015 22:44:16
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Produits pesque carrés (Difficile)
Biscuit n'est pas gâteau , je proposais une simple relance 
Vasimolo
#7 - 08-04-2015 23:33:05
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
produits presqur carrés (difficile)
@Shadock : je viens de le mailer.
@golgot : ça intuite, ça intuite ... 
#8 - 09-04-2015 00:37:40
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
produirs presque carrés (difficile)
Soit m la raison de la progression arithmétique
b=a+m et c=a+2*m
ab+1 = a^2+m*a+1 = (a+m/2)^2-m^2/4+1
ac+1 = a^2+2*m*a+1 = (a+m)^2-m^2+1
cb+1 = a^2+3*m*a+2*m^2+1 = (a+3*m/2)^2-m^2/4+1
Pour que ces 3 termes soient des carrés, il faut m^2=4 et m^2=1, ce qui est impossible.
A mois d'avoir loupé un truc, je conclurais qu'il n'existe pas de solution à ce problème.
#9 - 09-04-2015 08:27:15
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Produits presque carrés (Difficiel)
@kosso_tg: et pourtant si. la somme d'un carré plus quelque chose peut être carrée même si le quelque chose n'est pas nul !
Par exemple , 4+x est carré pour x=0 mais aussi x=5 ou encore x=12
Ce que tu devrais dire, c'est qu'il est impossible d'obtenir ces carrés là en particulier
#10 - 09-04-2015 23:41:23
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
rPoduits presque carrés (Difficile)
J'en ai 1 de plus !
15; 112 et 209 : (97 d'écart)
15*112+1=41²
15*209+1=56²
112*209+1=153²
Edit : Encore 2 !
56; 418 et 780 : 362 d'écart !
et
209; 1560 et 2911 : 1351 d'écart...
Bon, reste à comprendre pourquoi !
#11 - 09-04-2015 23:47:23
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Produits presqe carrés (Difficile)
Oui, tu as parfaitement raison, je suis allé trop vite en besogne 
En m'aidant d'excel, j'ai trouvé 3 cas:
a=premier nombre de la progression arithmétique et m le pas de la progression
a=0 et m=2
a=1 et m=7
a=4 et m=26.
En analysant de près l'évolution de a et m pour ces 3 cas, j'ai trouvé une relation que j'ai ensuite testée et qui marche. Un des ensembles solutions est donc:
[A(n),b,c] tels que b=A(n)+M(n), c=b+M(n) où (An) et (Mn) sont des suites définies comme ci après.
A(0)=0, A(1)=1 et A(n+2)=4*A(n+1)-A(n)
et
M(0)=2, M(1)=7 et M(n+2)=4*M(n+1)-M(n)
L'expression générale de ces suites permettent de définir les triplets pour tout n>=0
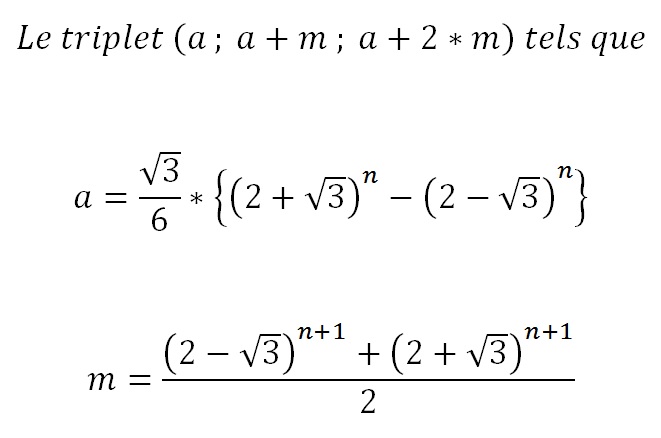
Voilà
#12 - 11-04-2015 10:58:13
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
produits oresque carrés (difficile)
Une petite recherche par EXCEL donne 2 triplets (a,b,c) solutions, associés aux triplets de carrés (A²,B²,C²):
(4,30,56)-------->(11²,15²,41²)
(15,112,209)---->(41²,56²,153²)
L'observation des 2 premiers laisse penser que 153² sera le 1er carré d'un nouveau triplet solution et en effet:
(56,418,780)----->(153²,209²,571²)
qui laisse présager une infinité de solutions.
Vérification
On remarque que (a,b,c)=(B-A,2B,3B+A)
On déduit les valeurs du triplet (A²,B²,C²)=(2B(B-A)+1;(B-A)(3B+A)+1; (2B+A)²)
Notons que le système d'égalités suivant se vérifie (en particulier C=2B+A):
2B(B-A)=A²-1
(B-A)(3B+A)=B²-1
2B(3B+A)=C²-1
On remarque que le second triplet (a',b',c') se déduit de (a,b,c):
(a',b',c')=(b/2,2c,4c-b/2).
Si on suppose que (a',b',c')=(B'-A');2B';3B'+A')=(B,6B+2A,11B+A) et C'=2B'+A' on en déduit:
A'=2B+A
B'=3B+A
C'=8B+3A
Vérifions que C'²-1=(2c)(4c-b/2)+1
(8B+3A)²=(6B+2A)(11B+4A)+1
se ramène à 2B(B-A)=A²-1 qui est la 1ère égalité du système précédent. Donc OK.
On fait de même avec (B'²-1) et (A'²-1)---->OK
Conclusion:
Si on a trouvé un 1er triplet (B-A,2B,3B+A) associé aux (A²,B²,C²) alors en remplaçant (A,B,C) par (2B+A, 3B+A, 8B+3A) on a un autre triplet (A'²,B'²,C'²) associé à (B'-A', 2B',3B'+A') qui satisfait les conditions de départ.
Il y a une infinité de solutions.
NB: après relecture, je retrouve un triplet plus petit que le 1er énoncé:
(1,8,15)---->(3²,4²,11²) lui même issu du triplet trivial:
(0,2,4)---->(1²,1²,3²)
#13 - 11-04-2015 13:24:36
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
produits presque carrés (difdicile)
Il semblerait qu'à partir de 3 suites :
u0=1; v0=8; w0=15 et
u1=4; v1=30; w1=56,
On puisse effectivement construire une infinité de séries solution en choisissant à chaque fois :
u(n)=4*u(n-1)-u(n-2); v(n)=4*v(n-1)-v(n-2); w(n)=4*w(n-1)-w(n-2)
donc : u2=4*4-1=15; v2=4*30-8=112 et w2=4*56-15=209, etc.
Mais je n'arrive pas à le démontrer pour le moment...
#14 - 11-04-2015 21:18:30
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Produits presque carré s(Difficile)
@kosso_tg: "formule que j'ai testée et qui marche", ça n'est pas une démonstration 
@nodgim : c'est une bonne réponse, mais comme je le disais tu démontres qu'un résultat trouvé par intuition se vérifie. Ça n'en est pas moins correct pour autant. Aurais-tu une démonstration directe du résultat ? (i.e. sans partir de la fin ?)
J'ajoute un indice au passage
#15 - 12-04-2015 08:17:40
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
produits ptesque carrés (difficile)
Scarta, non, mais ce que je fais est la preuve par récurrence. C'est aussi rigoureux qu'une preuve directe. Mais nettement moins élégant, je l'admets....
Rigoureusement, Scarta, a,b,c en progression arithmétique, c'est (b-d),b,b+d, et en posant les équations:
(b-d)b=(A-1)(A+1)
(b-d)(b+d)=(B-1)(B+1)
b(b+d)=(C-1)(C+1)
Et là franchement c'est pas très parlant pour commencer....
#16 - 12-04-2015 12:06:56
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
produits presque carrés (fifficile)
La suite définie par u_0=1, u_1=4, u_{n+1}=4.u_n-u_{n-1} fournit une infinité de triplets de la forme ( u_n ; 2.u_{n+1} ; u_{n+2} ).
Les premiers triplets sont (1;8;15), (4;30;56), (15;112;209).
On démontre que ça fonctionne par récurrence. Par exemple, pour montrer que ab+1 est un carré, on démontre par récurrence que :
u_n.2.u_{n+1}+1 = (u_{n+1}-u_n)², ce qui équivaut à u_{n+1}²+u_n²-4.u_{n+1}.u_n = 1.
Or u_{n+1}²+u_n²-4.u_{n+1}.u_n = (4.u_n-u_{n-1})²+u_n²-4.(4.u_n-u_{n-1}).u_n = 16.u_n²+u_{n-1}²-8.u_n.u_{n-1}+u_n²-16.u_n²+4.u_n.u_{n-1} = u_n²+u_{n-1}²-4.u_n.u_{n-1} = 1 par hypothèse de récurrence.
D'où je sors ça ? J'ai fait un rapide programme pour trouver les premiers termes de la suite, puis j'ai trouvé le lien qu'ils avaient entre eux. Ça vaut ce que ça vaut, mais ça marche 
#17 - 12-04-2015 17:50:25
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Produits presque carrés (Difficiel)
@Ebichu: même chose que précédemment : c'est juste mais non démontré.
@nodgim: oui, comme je le disais ça n'en est pas moins correct pour autant.
Sauf que pendant 4 ans j'étais resté sur une demo par récurrence (pas aussi simple que la tienne), alors qu'il existe une démonstration simple directe : c'est celle là que je voulais vous faire partager
#18 - 12-04-2015 18:27:27
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
produits presque carrés (diffucile)
C'est fort, Scarta, car elle est bien cachée cette preuve directe....
#19 - 12-04-2015 18:34:40
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Produits pesque carrés (Difficile)
Tiens, ton problème m'a fait poser une question: existe t'il aussi des solutions avec un quadruplet, quintuplet, ...?
Il semble que ce soit abordé dans le 1er msg que tu as cité, et que la résolution vient de Mr Euler. C'est donc du haut niveau...
#20 - 12-04-2015 19:22:08
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Produits presque carrés ((Difficile)
@scarta : quand tu dis que ce n'est pas démontré, c'est parce que je n'ai pas écrit la démo en entier, ou parce que tu veux une démo "directe" ? Dans ce dernier cas, je rends mon tablier, l'arithmétique et moi ça fait 10 
#21 - 12-04-2015 20:35:23
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Produuits presque carrés (Difficile)
Bon, toujours pas de démo, mais une construction plus simple
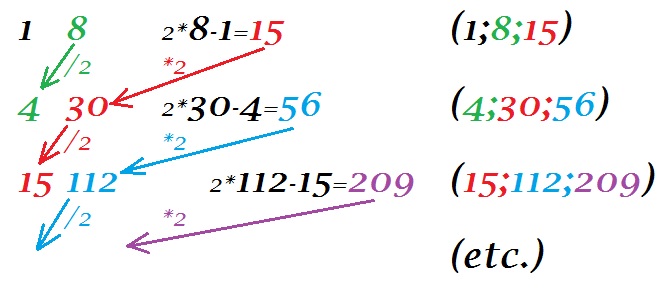
#22 - 13-04-2015 08:05:37
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Produits presque carré s(Difficile)
@Ebichu : les 2. Mais le 1er serait déjà pas si mal.
@nodgim : et pourtant j'ai moi-même été surpris de la trouver.
Regarde l'indice si tu veux.
Et je ne pense pas qu'il existe de quadruplets mais c'est intéressant à regarder
#23 - 13-04-2015 14:16:23
- Ebichu
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 888
Prdouits presque carrés (Difficile)
Je suis surpris que tu ne considères pas comme acquise la fin de la démonstration. Ça ne me dérange pas de détailler, mais de mon point de vue, la difficulté ne réside pas ici, plutôt dans le fait de trouver la suite.
* a, b, c sont en progression arithmétique car c-b=u_{n+2}-2*u_{n+1}=4.u_{n+1}-u_n-2*u_{n+1}=2*u_{n+1}-u_n=b-a (il suffit d'utiliser une unique fois la relation de récurrence linéaire qui définit la suite).
* bc+1 est un carré car bc+1 = 2.u_{n+1}.u_{n+2}+1 = (u_{n+2}-u_{n+1})², c'est la même relation que pour ab+1 mais décalée d'un indice.
*ac+1 est un carré car ac+1 = u_n.u_{n+2}+1 = u_n.(4.u_{n+1}-u_n)+1 = 4.u_{n+1}.u_n-u_n²+1 = u_{n+1}², car on a démontré dans le cas de ab+1 que u_{n+1}²+u_n²-4.u_{n+1}.u_n = 1. Là encore, on utilise une seule fois la relation de récurrence linéaire.
#24 - 13-04-2015 15:17:34
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
Produits presque carrés (Difficlie)
C'est vrai que sans Latex, j'ai eu du mal à lire, et donc j'ai lu trop vite. Donc oui, après relecture, je suis ok 
#25 - 13-04-2015 18:23:42
- scarta
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1986
produits ptesque carrés (difficile)
Bon, alors bonnes réponses de quasi tous, avec des démos plus ou moins par récurrence à chaque fois. Voici la démo "directe" que je vous propose.
On considère a et b deux entiers tels que ab+1=q² avec q entier positif.
On pose c=a+b+2q
ac+1 = a²+2aq+ab+1 = a²+2aq+q² = (a+q)²
bc+1 = b²+2bq+ab+1 = b²+2bq+q² = (b+q)²
Par conséquent, a et b étant fixés, on trouvera toujours un c qui vérifie ac+1 et bc+1 carrés.
Si maintenant on ajoute la dimension "progression arithmétique", de raison r, on a
c=b+r donc
r=a+2q
De plus, b=a+r=2a+2q, donc ab+1 = 2a²+2aq+1=q²
C'est une équation du second degré, en a comme en q, mais on va se focaliser sur l'équation en q:
q²-2aq-(1+2a²)=0
Discriminant réduit : 3a²+1 = z²
Solutions: a+z et a-z
On a a²<3a²<z² donc a<z et comme q>0, alors q=a+z
Encore faut-il que a soit tel que 3a²+1 soit carré.
On a z²-3a²=1. C'est une équation de Pell. Pas besoin de la forme complète de la solution, juste de savoir que si on trouve une solution A(0) et Z(0), alors on peut en avoir une infinité avec
Z(n+1)=3A(0)A(n)+Z(0)Z(n) et
A(n+1)=Z(0)A(n)+A(0)Z(n)
Il n'est pas souvent simple de trouver une solution initiale à tatons. Mais ici, c'est trivial : 4-3=1 donc A(0)=1, Z(0)=2
On a donc les 2 relations de récurrence suivantes:
A(n+1)=2A(n)+Z(n) et
Z(n+1)=3A(n)+2Z(n)
On pourrait s'arreter là : ayant une infinité de valeurs pour a, desquelles on déduit les valeurs de b et c, répondrait au problème.
Mais allons plus loin: trouvons les suites de q, b et c qui correspondent
Q(n) = A(n)+Z(n)
B(n) = 2A(n)+2Q(n) = 4A(n) + 2Z(n)
C(n) = B(n) + A(n) + 2Q(n) = 7A(n)+4Z(n)
Donc, A(n+1) = 2a(n)+Z(n) = B(n)/2
De plus, B(n+1) = 4A(n+1) + 2Z(n+1) = 14A(n)+8Z(n) = 2C(n)
Par ailleurs, par construction, C(n) = 2B(n)-A(n)
Enfin, la première solution de notre équation (pour a=1) nous donne le triplet (1;8;15). On trouve donc le résultat suivant :
- première solution : a=1; b=8; c=15
- solution suivante : a'=b/2; b'=2c; c'=2b'-a'
Premiers résultats : (1;8;15), (4;30;56), (15;112;209), (56;418;780), ...
Les démonstrations par récurrence sont bien évidemment correctes mais :
- dans le cas général, cela nécessite d'avoir l'intuition du résultat. Ce n'est pas toujours possible !
- dans ce cas précis, la démonstration directe nous permet un résultat supplémentaire, que je n'ai pas indiqué ici car je trouve le résultat actuel plus élégant : c'est la formule directe. En effet, on peut résoudre l'équation de Pell via des formules qui nous donnent alors A(n) et Z(n) sans avoir besoin de calculer les termes intermédiaires. Cf le résultat de kossi_tg.
Si la question était : "trouver un tel triplet tel que a comporte plus d'un million de chiffres, en base 10", la simple récurrence permet de prouver mais pas de trouver.
|
 |

 Accueil
Accueil
 Forum
Forum