Bravo à tous ceux qui ont tenté de résoudre ce problème (au moins dans un sens).
Voici une démonstration pour les deux sens:
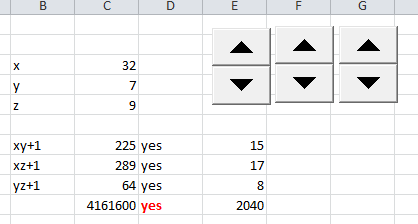
On suppose qu'il existe des triplets x,y,z qui vérifient
* [latex]x \leq y \leq z[/latex].
* (1+xy)(1+yz)(1+xz) est un carré
* 1+xy, 1+yz, 1+xz ne sont pas tous des carrés
Première remarque, si x=0, (1+yz) est a la fois carré et non carré, donc [latex]0 \lt x \leq y \leq z[/latex]
On pose [latex]s = x+y+z+2.x.y.z - 2\sqrt{(1+xy)(1+yz)(1+xz)}[/latex]
s est un entier puisque sous la racine on a un carré
On pose aussi[latex]s' = x+y+z+2.x.y.z + 2\sqrt{(1+xy)(1+yz)(1+xz)}[/latex]
s et s' sont 2 racines d'une équation du second degré, qu'on va déterminer
[TeX]N^2 -N (s+s') +ss' = 0\\
N^2 -2N(x+y+z+2xyz) + ((x+y+z+2xyz)^2-4(1+xy)(1+xz)(1+yz)) = 0\\
N^2 -2N(x+y+z+2xyz) + (x^2+y^2+z^2 - 2xy -2yz -2xz -4) = 0[/TeX]
S est solution de ce polynôme, qui peut aussi s’écrire de la manière suivante
[TeX]x^2 +y^2 +z^2 +s^2 -2(xy +yz +zx +sx +sy +sz) -4xyzs -4 = 0[/TeX]
On va s’intéresser à
[TeX](x+z-y-s)^2 = x^2 +y^2 +z^2 +s^2 +2xz -2xy -2xs -2yz -2zs +2ys[/TeX]
Du coup, notre polynôme devient
[TeX](x+z-y-s)^2 -4xz -4sy - 4xyzs -4 =0\\
(x+z-y-s)^2 = 4(xz+sy+xysz+1)\\
[/TeX]
Résultat (1.1):
[TeX](x+z-y-s)^2 = 4(xz+1)(sy+1)[/TeX]
De la même manière, on peut s’intéresser à (y+z-x-s) ou a (x+y-z-s) et notre polynôme devient
Résultats (1.2) et (1.3):
[TeX](y+z-x-s)^2 = (x+s-y-z)^2 = 4(yz+1)(sx+1)\\
(x+y-z-s)^2 = 4(xy+1)(zs+1)\\
[/TeX]
On va multiplier nos deux expressions (1.1) et (1.2) entre elles
[TeX](x+s-y-z)^2 (x+z-y-s)^2= 16(xz+1)(yz+1)(sx+1)(sy+1)\\
(xy+1)^2 (x+s-y-z)^2 (x+z-y-s)^2= 16(xz+1)(yz+1)(xy+1) . (xy+1)(sx+1)(sy+1)
[/TeX]
La partie de gauche est un carré, 16 est un carré et (xy+1)(xz+1)(yz+1) est un carré d'après notre hypothèse de départ, donc
Résultat (2):
(xy+1)(sy+1)(sx+1) est aussi un carré
D'après le résultat 1.1, si sy+1 est un carré, alors xz+1 aussi
D'après le résultat 1.2, si sx+1 est un carré, alors yz+1 aussi
D'après nos hypothèses de départ, si xz+1 et yz+1 sont des carrés, alors xy+1 n'en est pas un
Résultat (3):
Au moins un des termes du produit (xy+1)(sy+1)(sx+1) n'est pas un carré
D'apres le résultat 1.3, on a
[TeX](x+y-z-s)^2 = 4(xy+1)(zs+1)\\
zs+1 = \frac{(x+y-z-s)^2}{4(xy+1)}\\
zs+1 >= 0\\
s >= -\frac{1}{z}\\
[/TeX]
Si s=-1, alors x=y=z=1, ce qui est impossible, 8 n’étant pas un carré.
Si s=0, alors d’après les resultats 1.1, 1.2 et 1.3, les trois termes xy+1, yz+1 et xz+1 sont des carrés, ce qui est aussi impossible car contraire à nos hypothèses de départ
Résultat (4):
s>0
Par conséquent, d'après les résultats 2, 3 et 4
Résultat (5):
Si (x,y,z) est un triplet valide, (x,y,s) en est un autre (pas forcément dans cet ordre, puisque l'ordre est une de nos hypothèses, mais bon)
D'autre part, on a
[TeX]ss' = x^2+y^2+z^2 - 2xy -2yz -2xz -4 = \\
ss' = z^2 -x(2z-x) -y(2z-y)-4\\
ss' \lt z^2
[/TeX]
En effet, comme [latex]x \leq y \leq z[/latex], [latex]2z-x \gt 0[/latex] et [latex]2z-y \gt 0[/latex]
De plus, comme s < s', [latex]s^2 \lt z^2[/latex]
Résultat (6)
0<s<z
Du coup, on a quoi ? D'apres les résultats 5 et 6, si (x,y,z) est un triplet valide, (x,y,s) en est un autre, et x+y+z > x+y+s
Si pour un certain n, il existe un triplet x,y,z tel que x+y+z = n, alors il existe un n'<n qui possède aussi un triplet x,y,s tel que x+y+s = n'
D'apres l'argument de la descente infinie, c'est impossible et donc aucun triplet x,y,z de ce genre n'existe.
L'autre sens de la démonstration est trivial (un produit de carrés est un carré)
CQFD
Pour rappel:
la descente infinie est un argument qui dit:
Soit une propriété P sur les entiers naturels, si P(n) => P(n') avec n'<n, alors P est toujours fausse.
Présentée différemment: Si {n / P(n)} est non vide, il admet un plus petit élément p0. Si P(n) => P(n') avec n'<n, alors P(p0) => P(p0') avec p0' plus petit que le plus petit élément, ce qui est absurde.
Petite remarque 1: la grande différence entre les deux cas "1+xy, 1+yz, 1+xz sont / ne sont pas des carres" se situe dans le cas où on elimine s=0 dans cette démonstration
En effet, si on a 3 carrés, alors notre s est nul, et du coup (x,y,s) n'est pas un triplet, donc l'argument de la descente infinie ne peut pas s'appliquer dans ce cas là.
Petite remarque 2: Mais du chapeau de quel magicien ai-je sorti la formule de s ???
Tout simplement du chapeau du plus grands des "mathémagiciens": Euler.
En effet, il s'est un jour interessé au problème suivant:
soit un ensemble d'entiers tels que le produit de deux quelconques d'entre eux soit égal à un carré moins 1
Comment passer d'un ensemble de 3 éléments à 4 éléments? Tout simplement en construisant un tel s.
Petite remarque 3 (sources): Ce problème (tiré du PEN) a été posé et résolu par Kiran S. Kedlaya, du MIT, en 1998 dans Mathematic Magazine
Accueil
Le PEN, ou Problems in Elementary Number Theory (personne ne sait où est passé le "T" ??) est une collection de problèmes, mais alors vachement hards
