Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 02-08-2011 01:26:21
vois avez une petite faim ?C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#0 Pub#2 - 02-08-2011 08:52:48
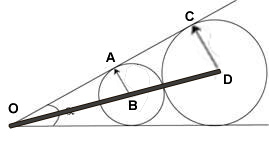
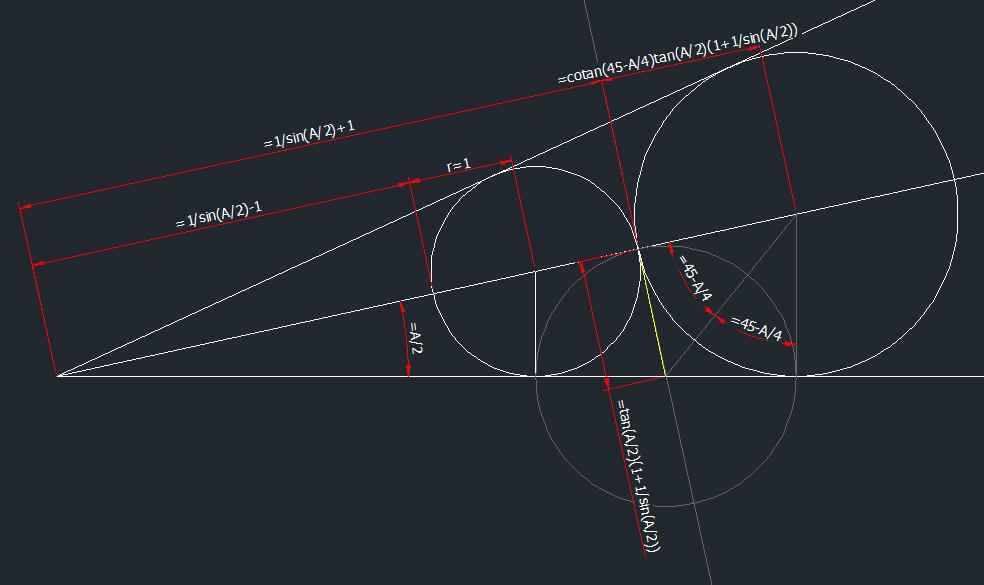
vous avez une petite faum ?En notant O le sommet du cône, I et J les centres du petit cercle et du grand cercle, A le point tangent du cône avec le petit cercle et B le point tangent du cône avec le grand cercle. Notons de plus que r=IA et R=JB, on obtient: #3 - 02-08-2011 09:01:00#4 - 02-08-2011 09:30:52#5 - 02-08-2011 10:06:45
vous avez une petote faim ?Soit O le centre du cercle de rayon 1 et O'le centre u cercle de rayon R, A le point d'in,tersection des 2 droites et A et B les points de tangence #6 - 02-08-2011 10:33:27
Vous avez une petite fai m?Bonjour Saint-Pierre, J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit. #7 - 02-08-2011 13:58:58
Vous avez une eptite faim ?
The proof of the pudding is in the eating. #8 - 02-08-2011 17:11:34
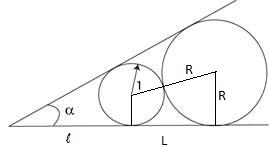
vous avez yne petite faim ?Je dirais (R2 le rayon du grand cercle) = 1 / tan(60/2) = 1 / tan(30) #9 - 02-08-2011 17:12:09
Vous avez unee petite faim ?
#10 - 02-08-2011 20:08:07
Vous avez une peite faim ?Bonjour, #11 - 03-08-2011 10:23:57
Vous avz une petite faim ?Bonjour tout le monde, #12 - 03-08-2011 12:05:58
oVus avez une petite faim ?Soit x la distance du sommet de alpha au centre du petit cercle. Réponse rapideSujets similaires
Mots clés des moteurs de recherche
|
 | |||||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.