 |
#1 - 31-08-2011 15:07:47
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
invitation à lz géométrie...
Le côté du carré vaut 1 mètre. Quel est le rayon, en cm, d'un cercle bleu ?

C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#2 - 31-08-2011 15:29:25
- gabrielduflot
- Expert de Prise2Tete
- Enigmes résolues : 34
- Messages : 614
invitation à la géolétrie...
en notant r le rayon du cercle
par rapport à la diagonale du carré qui vaut[latex]\sqrt 2[/latex]
on a sur la diagonale en tracant les rayons des cercles:
2 diagonales d'un carré de côté r
deux hauteurs d'un triangle équilatéral de côté 2r
la longueur d'un carré de côté 2r
[TeX](2\sqrt 2 + 2\sqrt 3 + 2)r=\sqrt 2[/latex] d'où [latex]r=\frac{\sqrt 2}{2\sqrt 2 + 2\sqrt 3 + 2}[/TeX]
#3 - 31-08-2011 15:47:52
- esereth
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 176
Initation à la géométrie...
Bonjour,
Un premier calcul me donne
[TeX]\frac{1}{2+\sqrt{2}+\sqrt{6}}[/TeX]
J'explique :
J'appelle r le rayon cherché.
les 4 cercles du centre forment un carré de côté 2r
Les trois cercles en haut à gauche forment un triangle équilatéral de coté 2r
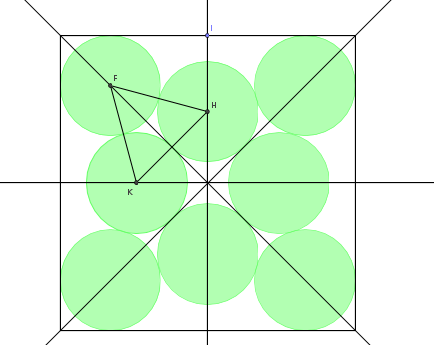
J'appelle F le centre de celui en haut à gauche, H celui en haut au milieu et K celui à gauche au milieu.
L'angle IHF mesure 180°-45°-60°=105°.
Donc (FH) fait un angle de 15° avec l'horizontale.
En projetant sur l'horizontale on a donc :
[TeX] r+2r\cos \frac{\pi}{12}=\frac{1}{2}[/TeX]
et on a [latex]\cos \frac{\pi}{12}=\frac{\sqrt{2}+\sqrt{6}}{4}[/latex]
D'où :
[TeX] r(2+\sqrt{2}+\sqrt{6})=1[/TeX]
#4 - 31-08-2011 16:31:26
- BilouDH
- Habitué de Prise2Tete
- Enigmes résolues : 46
- Messages : 29
incitation à la géométrie...
Bonjour,
Je trouve un rayon de 0.17, enfin 1/(2+4cos(15°)).

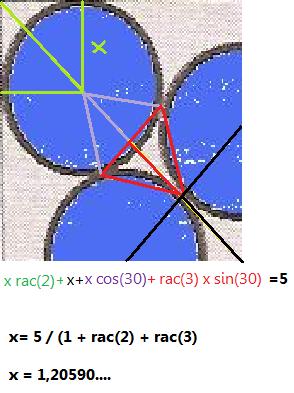
Les segments jaunes mesurent chacun r.
Les segments verts mesurent chacun 2r.
L'angle entre le segment vert et le segment rouge mesure donc 15° car le triangle vert est equilateral.
Le segment rouge mesure donc 2*cos(15°)*2*r.
On obtient donc 1=2r+4r*cos(15°) donc r=1/(2+4cos(15°))=0.17
#5 - 31-08-2011 17:22:07
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Invitation à la géométre...
Rebonjour,
Soient R le rayon d'un cercle bleu et C le côté du carré.
On aura: C = 2R + 4R cos 15°
Or on a: cos 15° = V((1 + cos 30°)/2) avec cos 30° = V3 / 2
Donc: cos 15° = V(2+V3) / 2 = V2 / 4 + V6 / 4
Finalement: C = R (2 + V2 + V6)
AN: C = 100 cm donne R = 17,05 cm env.
Rebonne journée.
Refrank
Edit: j'avais oublié de conclure (ou de répondre à la question).
#6 - 31-08-2011 17:46:50
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Invitation à la éométrie...
C'est bon, sauf pour gabriel.
Franky, tu as oublié de conclure. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#7 - 31-08-2011 17:51:58
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
nvitation à la géométrie...
Pour savoir si on ne s'est pas trompé :
Il y a 8 cercle de rayon R inscrit dans un carré de côté 100cm on résous donc l'équation [latex]8\pi R^2=100^2[/latex] et on trouve un ordre d'idée du maximum à ne pas dépasser qui est [latex]R_0 < \frac{25\sqrt{2}}{\sqrt{\pi}} = 19.95[/latex] environ.
Application :
Sans faire de détails j'arrive à [latex]\fbox{\blue{r_0=\frac{25.\sqrt{2}}{2}=17.68}}[/latex] environ.
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#8 - 31-08-2011 19:39:24
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
invitayion à la géométrie...
Je trouve rac2/(2rac2+2+2rac3)=0.17054 m en passant par le calcul de la diagonale.
#9 - 31-08-2011 19:46:47
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Inivtation à la géométrie...
C'est sympa de dire que "j'ai oublié de conclure".
En réalité, je n'avais pas répondu à la question !!!
Erreur rectifiée dans l'édit du message initial.
Comme quoi ... on (je) ne lis pas assez les textes.
Bonne soirée.
Frank
#10 - 02-09-2011 16:22:26
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
invitatiob à la géométrie...
Oui à nodgim et à Shadock: tes décimales ne sont pas bonnes. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#11 - 02-09-2011 16:43:31
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Invitatiion à la géométrie...
Le résultat est juste mais les décimales sont fausses ?  j'ai refais le calcul et en arrondissant à deux chiffres après la virgule j'ai bien 17.68.... j'ai refais le calcul et en arrondissant à deux chiffres après la virgule j'ai bien 17.68....
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#12 - 02-09-2011 16:46:41
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Invitatio nà la géométrie...
Le résultat n'est pas bon. Le premier nombre est juste, mais ça ne suffit pas. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#13 - 02-09-2011 20:32:12
- FyeD.Flowright
- Amateur de Prise2Tete
- Enigmes résolues : 16
- Messages : 1
invitation à la géométrir...
En supposant que les cercles soient "tassés" au maximum, je me permets de supposer, de par la forme des interstices, que les centres des cercles du milieu forment un carré, et que les centres des autres cercles bleus forment des triangles équilatéraux une fois reliés aux centres des carrés du milieu (je sais : je suis assez confus et j'en deviens dur à suivre ^^). De plus, à chaque coin du grand carré il y a un petit carré ayant pour sommets opposés le sommet du grand carré et le centre du cercle le plus proche, ce petit carré est intéressant car il a pour mesure du côté le rayon du cercle.
Je raisonnerai à partir de maintenant en CENTIMETRES
Si on étudie la diagonale du grand carré (une seule, vu que la deuxième c'est la même xD), on constate qu'elle peut être divisée symétriquement en 5 parties :
- à chacun des bouts : la diagonale du petit carré, qui mesure donc (racine de 2)*r, où r est le rayon des cercles
- après ces deux bouts, la hauteur des triangles équilatéraux reliant les centres des cercles, de valeur (racine de 3)*r, puisque le triangle a pour côté 2r
- la diagonale du carré reliant les centres des cercles du milieu, de valeur 2*(racine de 2)*r puisque le carré a pour côté 2r
Ainsi la diagonale mesure 2*(racine de 2)*r+2*(racine de 3)*r+2*(racine de 2)*r, soit 4(racine 2)r + 2(racine 3)r
Or elle mesure également 100(racine 2) car elle est la diagonale du carré de côté 100.
Par transformation d'égalité, on obtient r = 100/(4+(racine 6)), ou encore
r = 40 - 10(racine de 6) cm (en arrondissant : 15,505102572168219018027159252941)
Vu l'aspect chaotique de mon résultat je suis ouvert à toute suspicion d'erreur du fait de ma démarche ... toute aussi chaotique ^^'
#14 - 02-09-2011 22:14:00
- halloduda
- Professionnel de Prise2Tete
- Enigmes résolues : 24
- Messages : 495
- Lieu: Ardèche
invitation à la géométroe...
[TeX]r=\frac {100}{2+\sqrt 2+\sqrt 6}\approx 17.054 cm[/TeX]
#15 - 03-09-2011 13:40:56
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Invitation à al géométrie...
Oui, bonne réponse, halloduda. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#16 - 03-09-2011 14:10:59
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
Invitation la géométrie...
euh, c'est 5 rac(2) donc r = 1,70554....
#17 - 03-09-2011 15:34:42
- TiLapiot
- Expert de Prise2Tete
- Enigmes résolues : 16
- Messages : 852
- Lieu: au terrier ;^)
Invitation à la géométrie..
#18 - 03-09-2011 16:01:19
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Invitation à la géométre...
C'est, en tout cas, la bonne réponse, TiLapiot. 
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#19 - 03-09-2011 16:02:28
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
invitayion à la géométrie...
gwen27 a écrit:euh, c'est 5 rac(2) donc r = 1,70554....
Non, c'est bien 17 cm...
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#20 - 03-09-2011 17:06:00
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
invitation à lz géométrie...
Oui, mal lu, j'ai tout fait avec 10 m au lieu d'un .
#21 - 03-09-2011 17:13:15
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
Innvitation à la géométrie...
C'est uniquement chez moi ou les formules Latex ne s'affichent pas ???
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#22 - 03-09-2011 17:15:33
- SaintPierre
- Banni
- Enigmes résolues : 42
- Messages : 2063
- Lieu: Annecy
Invitation à la géoométrie...
Disons que, parfois, elles ne s'affichent pas tout de suite...
C'est à l'intelligence d'achever l'oeuvre de l'intuition.
#23 - 03-09-2011 17:55:38
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Invitaton à la géométrie...
SHTF47 a écrit:C'est uniquement chez moi ou les formules Latex ne s'affichent pas ???
Moi aussi je suis sur chrome et depuis hier aprem ça ne s'affiche pas.
Par rapport à l'énigme j'avais plutôt pensé que le diamètre de deux cercles mi bout à bout revenait à calculer la longueur d'une demi diagonale et puis de diviser par 4 d'où mon résultat.
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#24 - 04-09-2011 20:04:22
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Invvitation à la géométrie...
C'est rassurant tout ça: je ne suis pas le seul à ne pas lire correctement l'énoncé !!!
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum










