Forum dédié aux énigmes et à toutes formes de jeux de logique. | Déconnexion |
|
Tu n'es pas identifié sur Prise2tete : s'identifier.  Accueil Accueil
 Forum Forum
|
 |
#1 - 15-04-2010 01:13:28
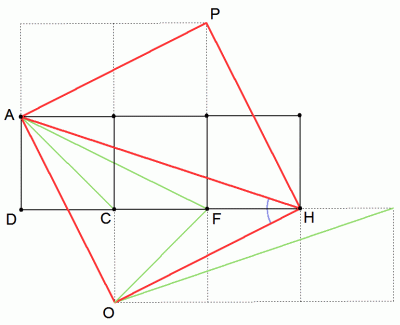
Géométtrie pour les nuls! 1On forme 3 carré accolés ABCD ; BEFC ; EGHF ( les points A,B,E,G sont alignés de même pour D,C,F,H). "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#0 Pub#2 - 15-04-2010 04:02:32
géométrie pour les nulq! 1Bon alors trigo brute sur des carrés de côté 1 juxtaposés. Il aurait pu pleuvoir, con comme il est ! (Coluche) #3 - 15-04-2010 05:12:42
gépmétrie pour les nuls! 1Bonjour à tous, #4 - 15-04-2010 09:11:33
Gééométrie pour les nuls! 1Ayant résolu le problème avec la méthode tan(a+b), j'ai cherché et trouvé la meilleure source possible : http://pagesperso-orange.fr/debart/geop … html#af199 Celui qui fuit les casse-tête ne vaut pas un clou. #5 - 15-04-2010 11:24:39
Géométrie pour les uls! 1J'ai fait la figure, pour le reste je trouve (un peu de trigo ne faisant pas de mal) : Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #6 - 15-04-2010 14:11:06
géométeie pour les nuls! 1après des calculs trigonométriques [latex]tan (\widehat{HAB})={1\over3}[/latex]; [latex]tan(\widehat{HBE})={1\over2}[/latex]; [latex]tan(\widehat{HEG})=1[/latex] donc [latex]\widehat{HEG}[/latex]=45° #7 - 15-04-2010 14:20:40#8 - 15-04-2010 14:55:16
Géométrie pou rles nuls! 1Faute mieux, je dirai que Atan(1)=Atan(1/2)+Atan(1/3). #9 - 15-04-2010 18:53:23
Géométrie pour lles nuls! 1Une façon amusante et sans calcul pour le montrer : #10 - 16-04-2010 09:15:07
géométrie pour les nuld! 1Une solution facile mais complexe : (3-i)(2-i)=5(1-i) #11 - 16-04-2010 13:44:07
Géoémtrie pour les nuls! 1Bravo à tous sauf à Piode qui pour le moment n'a pas trouvé la réponse
. Vasimolo arrive à le faire sans calculs bravo!!!! "L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline #12 - 16-04-2010 14:46:49
Géométrie pou rles nuls! 1Salut : #13 - 16-04-2010 16:36:23#14 - 16-04-2010 17:51:05
géométriz pour les nuls! 1Et de deux Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #15 - 16-04-2010 21:04:19
géométrie pour les nuks! 1c'est du Thales tout craché. A, B, E, G alignés et AB = BE = EG #16 - 16-04-2010 23:28:45
Géométrie pour les unls! 1C'est un problème que je trouve vraiment très intéressant #17 - 17-04-2010 00:18:10
Géométrie pour les nuls!Voila, finalement, la demonstration est simple: Great minds discuss ideas; Average minds discuss events; Small minds discuss people. -Eleanor Roosevelt #18 - 17-04-2010 11:56:48
Gééométrie pour les nuls! 1Je m'en sors par les tangentes "Je ne lis jamais un livre dont je dois faire la critique. On se laisse tellement influencer." O. Wilde #19 - 18-04-2010 12:19:52
Géométrie pour les nul!s 1Voici ma démonstration. #20 - 19-04-2010 10:20:12
Géométrie pour les nusl! 1
"Être une enzyme avec fonction hydrolyse, mais ne pas savoir comment si prendre ..." #21 - 21-04-2010 15:22:18#22 - 21-04-2010 20:16:43
géométrie pour les nuks! 1Ma démo n'était pas la plus courte, tiens Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #23 - 25-10-2010 10:15:07
Géomtrie pour les nuls! 1Comment démontrer que le point G est le centre de gravité du triangle ABC #24 - 25-10-2010 10:29:27
GGéométrie pour les nuls! 1Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298 #25 - 25-10-2010 10:51:00
Gééométrie pour les nuls! 1
Raisonnement par l'absurde : si ça n'était pas le centre de gravité, on l'aurait appelé autrement que G, par exemple D. J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit. Réponse rapideSujets similaires
Mots clés des moteurs de recherche |
 | |||||||||||||||||||||||||||||||||
| Prise2Tete Forum Statistiques Liste des membres Hall of Fame Contact | |||||||||||||||||||||||||||||||||||
Un jeu où seules la réflexion, la logique et la déduction permettent de trouver la solution.