Hello hello,
Je viens de griffonner un truc à ma pause café qui me fait encore me dire que les maths c'est vraiment beau et puissant. Le probleme maintenant bien connu de beaucoup ce trouve ici:
P2T Parking
Les meilleurs ont obtenu 112.
Je me disais qu'on pouvait certainement espérer mieux, alors j'ai cherché et puis je suis arrivé à démontrer en à peine quelques lignes que le maximum était ce 112 (dans le cas précis de la grille donnée dans l'énoncé).
Sauriez vous en faire autant ? :p (il y a du défi) (une vraie démonstration rigoureuse  )
)
Je poserais des indices au fur et à mesure sur les différentes étapes pouvant arriver à la démonstration.
Bonne chance aux matheux qui tenteront!
Indice 1 (petit indice):
Spoiler : [Afficher le message] Tentez de voir le problème de manière moins spécifique dans un premier temps pour avoir une majoration, puis la rendre plus fine pour notre cas spécifique, et éventuellement voir des cas particuliers à la main.
Indice 2 (un bon point de départ):
Spoiler : [Afficher le message] Sur une grille hexagonale illimitée, quelle est le plus grand nombre de places qu'un réseau connexe de n cases de route peut desservir?
Démonstration:
Spoiler : [Afficher le message]
Sur un reseau hexagonal illimité:
Lemme 1:
Un réseau connexe de N cases de route dessert au maximum 2N+4 places.
Démonstration du lemme:
On peut considérer qu'un réseau routier peut être construit itérativement
en greffant une case de route sur un réseau existant.

Sur la figure ci dessus, on greffe une nouvelle case route vert flashi sur une case quelconque du réseau existant, au bilan de la transformation: on a perdu une place et on en a gagné 3, donc un gain de 2 places.
En considérant que la démarche s'initialise avec une case de route desservant 6 places, le résultat du lemme vient clairement. (C'est une majoration qui en plus peut être très facilement atteinte).
Corolaire 1: On remarquera que pour avoir un réseau optimal on ne doit à chaque greffe jamais toucher plus d'une route du réseau précèdent et jamais toucher plus de 2 places non plus, tout manquement serait une désoptimisation
définitive.
Dans notre figure:
Si on considère nos N cases de routes à l'intérieur on en a nécessairement une qui touche l'entrée:

Cette case va donc perdre 3 places potentielles (marquées par les points bleus). En conclusion dans notre parking on ne peut desservir avec N routes que 2N+1 places (lemme 1b)
Il y a un autre facteur limitant dans le cas de notre figure c'est que le nombre de places desservies ne peut être supérieur au nombre de cases restantes. Il y a au total 169 cases, donc pour N routes on ne peut desservir au total que 169-N places.
On a donc le tableau suivant:
N 55 56 57
max desservi lemme 1b 111 113 115
cases restantes 114 113 112
En dessous de 55 routes, on voit que le lemme 1b devient limitant.
Au dessus de 57 routes, on voit que le nombre de cases restantes devient limitant.
Comme on a déjà atteint 112, il ne reste donc qu'a prouver qu'on ne peut pas atteindre 113 avec 56 places à l'intérieur. On remarque qu'on a absolument aucune marge d'erreur (la majoration est 113 et on doit faire 113), c'est à dire qu'on doit pouvoir construire itérativement notre réseau interne en faisant en sorte qu'a chaque ajout d'une route on gagne 2 places par rapport au précèdent.
Il vient donc que:
-Toute la périphérie doit être constituée de places. (si on route touchait la périphérie on perdrait au moins une place)
-Sur la figure suivante:
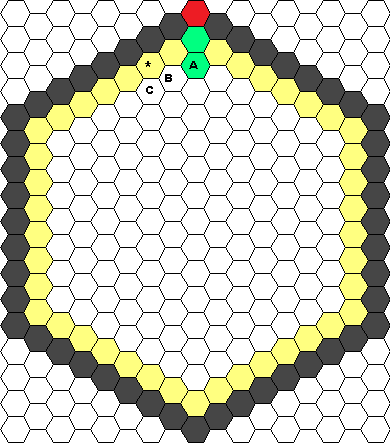
-Si B était une place alors C devrait être une route. (pour accéder à la place marquée étoile).
Hors si C était une case de route alors A et C desserviraient la même place B. (Alors que A et C ne se touchent pas). Conclusion on perdrait au moins une place par rapport à l'optimal (non respect du corolaire 1) et donc B ne peut pas être une place. c'est donc une route. On peut faire le même raisonnement avec la case suivante et ainsi de suite sur toute la seconde périphérie, démontrant que celle ci doit être de la route, et pointant la perte d'optimalité qu'on aurait lorsque cette route formerait une boucle. (non respect du corolaire 1.)
Conclusion: on ne peut pas faire 113 et par conséquent 112 déjà obtenu est le maximum.
CQFD.

 Accueil
Accueil
 Forum
Forum







