Enigme Paradoxe "impossible"? @ Prise2Tete

Promath- · #1

Le forum mathématiques meurt un peu, les problèmes ne fusent plus.

Je propose ce problème, dont je citerais la source.

A Eratoville 240 candidats des collèges Castor et Pollux passent une épreuve de mathématiques.
Il y a autant de filles que de garçons. Les deux collèges présentent autant de candidats l'un que l'autre.
Dans chacun des deux collèges les garçons ont un pourcentage de réussite qui excède de 20% celui des filles.
Pourtant le rectorat affirme que le succès général à l'épreuve a été de 20 % meilleur chez les filles.

"Les garçons ont des pourcentages meilleurs dans chacun des collèges !"

"Les filles sont les meilleures pour les deux collèges !"

Pas d'accord s'écrient les garçons, nous avons eu dans les deux collèges des pourcentages de réussite meilleurs de 20% sur les filles !
Pourtant ils ont tort, les filles sont bien les meilleures.
Pourquoi ?

Bonne chance!

nodgim · #2

"les garçons ont un pourcentage de réussite qui excède de 20% celui des filles."
Il faudrait quand même être plus précis. Personnellement, je ne vois pas à quoi s'adresse le 20%. Les autres phrases sont tout aussi ambigües...

gwen27 · #3

Il suffit que la répartion Garçons filles soit déséquilibrée.

Dès lors, un faible pourcentage de réussite dans l'école où il y a plein de garçons crée un faible écart en nombre et un fort taux de réussite dans l'école où il y a des filles crée un fort écart en nombre.

Au final, les filles ont mieux réussi.

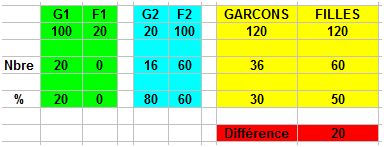
Il doit y avoir plein de solutions possibles. En prenant une répartition 100 pour 20 , on en trouve assez facilement une dont les nombres prennent des valeurs entières.

Promath- · #4

Bravo gwen.
Nodgim: les phrases me semblent très correctes, pour une fois c'est à dire, admettons 5 et 25 pourcent.

nodgim · #5

Alors si les phrases sont correctes, peut être as tu voulu dire cela ?

"Dans chaque collège, le nombre de garçons ayant réussi est 20% supérieur à celui des filles. Et pourtant, si on prend les 2 collèges ensemble, le nombre de filles ayant réussi est 20% supérieur à celui des garçons."

qui me semble bien plus précis.

Est ce bien ce la ou est ce autre chose ?

Promath- · #6

C'est cela.

Franky1103 · #7

Bonjour à tous,
On pourrait très bien avoir simultanément les deux évènements suivants (qui ne s'excluent pas):
1°) Le nombre de notes des garçons supérieur à la note éliminatoire est de 1,2 fois celui des filles.
2°) La moyenne des notes des filles est de 1,2 fois celle des garçons.
J'ai la fainéantise de donner un exemple, mais je pourrais le faire le cas échéant.
Bonne soirée.

Jackv · #8

Promath :
Le forum mathématiques meurt un peu, les problèmes ne fusent plus.

Du coup, je trouve que les énigmes mathématiques fusent beaucoup en ce moment !

C'est effectivement troublant à la première lecture , mais en y réfléchissant un peu, pas tant que cela !
Cela montre seulement que le collège où le pourcentage de fille était le plus grand a eu globalement des résultats supérieurs à l'autre .

EDIT : Par exemple, dans le collège A, 80 % des 90 filles ont bien passé l'épreuve soit 72 filles reçues ce qui est le cas de 100 % des 30 garçons, soit 30 garçons.

Et dans le collège B, 20 % des 30 filles ont bien passé l'épreuve soit 6 filles reçues ce qui est le cas de 40 % des 90 garçons, soit 36 garçons.

Au total, cela nous donne 78 filles OK contre seulement 66 garçons .

Merci Promath d'avoir attirer notre attention sur ce curieux paradoxe .

Promath- · #9

Bravo à tous d'avoir cherché!

nodgim · #10

nodgim a écrit:
Alors si les phrases sont correctes, peut être as tu voulu dire cela ?

"Dans chaque collège, le nombre de garçons ayant réussi est 20% supérieur à celui des filles. Et pourtant, si on prend les 2 collèges ensemble, le nombre de filles ayant réussi est 20% supérieur à celui des garçons."

qui me semble bien plus précis.

Est ce bien ce la ou est ce autre chose ?

Promath, es tu sûr que la réponse est compatible avec la reformulation que j'avais faite et que tu as validée ?

Promath- · #11

Oui.

Jackv · #12

Promath a écrit :
Je propose ce problème, dont je citerais la source.

Chose promise, chose promise !

gwen27 · #13

Non promath , le pourcentage de réussite des garçons excède bien de 20% celui des filles, c'est ce qui était dans l'énoncé. Mais pas leur nombre, ce qui était la question de nodgim.

MthS-MlndN · #14

Jackv a écrit:
Promath a écrit :
Je propose ce problème, dont je citerais la source.
Chose promise, chose promise !

Les promesses n'engagent que ceux qui y croient

Jackv · #15

C'est pourquoi je n'ai pas dit "chose due" !

Promath- · #16

lol
Moui.
Je dis la source ou alors je vous laisse mijoter encore un peu?
Je vous laisse mijoter.
Moui.
C'est cela.
Voici l'url
Ne cliquez pas!
Hihihi
Paradoxes,puis Interpretations trompeuses en bas à droite.

nodgim · #17

Promath est précoce en mauvaise foi, défaut qui apparait normalement plutôt avec l'âge...

Promath- · #18

Comment ça en mauvaise foi?

nodgim · #19

Je te laisse le bénéfice du doute et une lecture trop rapide que tu as faite de mes messages, que je t'invite à relire.

Sinon, quand on dit que telle proportion A est supérieure de x % à une autre B, alors ça veut dire A=(1+x)B.
Si on veut dire que A=x+B, alors on parle alors de points et non de pourcentages. Dans ton cas, tu aurais dû dire "de 20 points supérieur..."

Promath- · #20

C'était ce qu'il y avait d'écrit sur le site, et je l'ai bien compris.
Je comprends que ça ait pu poser quelques petits soucis; ça dépasse l'ICV de quelques uns.

Mais comment ça en mauvaise foi?

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#1 - 27-05-2012 19:27:52

paradoxe "impissible"?

#0 Pub

#2 - 28-05-2012 07:54:19

oaradoxe "impossible"?

#3 - 28-05-2012 08:40:29

paradoxe "imoossible"?

#4 - 28-05-2012 09:47:30

Paradoxe "impossible&quto;?

#5 - 28-05-2012 11:04:46

Pradoxe "impossible"?

#6 - 28-05-2012 19:07:45

Paradoex "impossible"?

#7 - 29-05-2012 22:47:31

Paradoxe "impossiible"?

#8 - 30-05-2012 12:50:45

Paradoxe "imppossible"?

#9 - 31-05-2012 17:34:38

Paradoxe "impossible"t;?

#10 - 31-05-2012 18:13:16

Paradoxe "imposssible"?

nodgim a écrit:

#11 - 31-05-2012 18:36:37

Paradoxe "impossible&quto;?

#12 - 31-05-2012 18:39:55

Paradoxe &"impossible"?

#13 - 31-05-2012 18:45:46

paradoxe "impodsible"?

#14 - 01-06-2012 11:06:09

paradoxz "impossible"?

Jackv a écrit:

#15 - 01-06-2012 13:00:07

Praadoxe "impossible"?

#16 - 01-06-2012 17:25:47

Paradoxe quot;impossible"?

#17 - 01-06-2012 18:13:22

Paradoxe &uot;impossible"?

#18 - 01-06-2012 20:32:37

paradoxe "imposdible"?

#19 - 02-06-2012 11:02:42

Paradoxe q&uot;impossible"?

#20 - 02-06-2012 12:14:21

Paradoxe ";impossible"?

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums