|
#101 - 23-10-2012 20:02:12
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Et ta soeur
Azdod a écrit:Ce sont les stats qui doivent s'approcher de la probabilité et non pas le contraire !
La preuve : La loi faible des grands nombres !
La réponse est 1 sur 2. Faut pas compliquer non plus !
Quand une théorie existe c'est le cas.
Quand aucune théorie n'existe ou qu'il en existe une pas assez précise, on prend comme probabilité la statistique observée, sans tenir compte de l'incertitude.
Cette histoire de 1/2 est en la meilleure preuve...
Quelle théorie justifie ce 1/2? Les stats ne le montrent pas non plus. Les faits sont tétus 
#102 - 23-10-2012 20:25:38
- godisdead
- Expert de Prise2Tete
- Enigmes résolues : 22
- Messages : 747
#103 - 23-10-2012 22:56:54
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Et ta seour ?
Soit je réponds 1/2 comme la plupart d'entre vous (sinon on risque d'avoir un problème avec la majorité des énigmes probabilistes futures dans lesquelles l'auteur n'aura pas mis tous les points sur les i)
Soit je réponds que la probabilité existe mais varie constamment pour des raisons biologiques, environnementales, sociologiques,... et ne peut donc être calculée par personne.
Dans tous les cas, ça réveille le forum 
#104 - 23-10-2012 23:02:58
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Et ta oeur ?
Une valeur qui existe mais qui varie constamment, ce n'est pas une valeur mais une fonction du temps 
Au fait, en admettant que la probabilité dans le contexte de cet exercice soit 1/2, je dis que la réponse à l'exercice est aussi 1/2 
#105 - 23-10-2012 23:55:01
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
Et ta sour ?
rivas a écrit:Quelle théorie justifie ce 1/2? Les stats ne le montrent pas non plus. Les faits sont tétus 
Et quelle théorie justifie le 1 sur 6 d'un dé équilibré ?
et quelle théorie justifie le 1 sur 2 d'un lancé d'une pièce équilibrée ?
...
Il y a un grand manque de vocabulaire ici !
Une probabilité est un nombre compris entre 0 et 1 qui caractérise le degré de la vraisemblance d'un évènement.
C'est vrai pour un dé le résultat d'un lancer correspond à la position du départ, la force du lanceur, le degré de frottement de la surface sur laquelle le dé atterrit ! Bon, il en a une infinité de facteurs pouvant influencer le résultat d'un lancer de dé, et si le joueur maîtrise tous ces facteurs, alors il peut obtenir le résultat voulu.
Mais puisque l'homme ne peut pas maîtriser tous ces facteurs réellement, Alors on a un petit nombre qui caractérise tous ça qui s'appelle probabilité !
Prends un dé et lance le 6000 fois; tu ne vas jamais obtenir 1000 fois chaque résultat, car 6000 est trop petite. Si tu Obtiens 999 fois le chiffre 1 cela ne veut pas dire que la probabilité d'obtenir 1 est de 999 sur 6000 : car cette même expérience peut être faite par un autre et les résultats seront complètement différent !
La loi faible des grands nombres nous affirme qu'il faut lancer un dé une infinité de fois afin d'avoir la proportion 1 sur 6. La notion de l'infini rend alors la notion de la probabilité trop loin des statistiques !
Dans notre cas, nous avons un problème de sexe qui est le résultat d'une expérience aléatoire (le X ou le Y) dont la science affirme qu'il n'y a aucune avantage pour le X que pour le Y! Si la probabilité d'un lancer d'un dé équilibré est de l'ordre de 1 sur 6 alors il n y a aucun problème de dire que la probabilité d'avoir une fille (ou respectivement un garçon) est de 1 sur 2.
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#106 - 24-10-2012 08:33:50
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Et ta ssoeur ?
@Azdod: Je te propose vraiment la lecture des liens que j'ai donné ci-dessus qui te permettront de clarifier les différences entre probabilité et statistiques. Surtout le second.
Je ne sais pas si c'est moi que tu essaies de convaincre mais je n'ai aucun problème de compréhension entre statistique et probabilité (enfin je pense  ). ).
Je sais très bien qu'une probabilité est un nombre réel compris entre 0 et 1, qu'en lançant 6000 fois un dé tu ne feras pas 1000 de chaque face (sauf coup de chance extraordinaire dont la probabilité est non-nulle). Je connais aussi l'ordre de grandeur de l'écart entre N/6 et le nombre d'apparitions d'une face lorsque N grandit. Je ne pense pas non plus ne pas connaitre le vocabulaire mathématique adéquat à cette discussion et je pense avoir été très précautionneux à utiliser le bon vocabulaire le plus souvent possible. J'ai relu mes textes plusieurs fois pour éliminer les coquilles de vocabulaire.
Par contre la probabilité n'a aucun rapport avec le fait que l'on ne maitrise pas tous les facteurs d'une expérience. C'est bien ça le problème. Faire cela c'est généraliser le constat d'une statistique et appeler cela une probabilité mais une probabilité mathématique ce n'est pas cela.
Pour un dé, la probabilité est 1/6 parce que le dé est homogène. C'est tout.
Si le dé était inhomogène et que je connaisse la répartition des masses et en particulier la position du centre de gravité, je pourrais donner les probabilité de chaque face sans faire de statistiques de lancer.
Les erreurs dont tu parles et qui ne se maitrisent pas sont à prendre en compte dans l'incertitude qui accompagne une statistique: expérience physique soumise aux contraintes physiques.
La confusion vient sans doute du fait que le mot probabilité a 2 utilisations: une dans le langage courant et pour la vie courante et une mathématique. Le mot probabilité dans le langage courant est utilisé comme généralisation du constat d'une statistique. En cela tu as raison. Ce qui est dangeureux parce que si l'expérience dont le résultat est entaché d'une erreur de méthode, on en déduit une "pseudo-probabilité" fausse. Une autre expérience sans cette erreur de méthode ou avec un autre erreur de méthode donnerait une autre probabilité. On en vient même dans le langage courant à parler de probabilité d'être élu basé sur les résultats d'un sondage. On parle parfois de probabilité statistique dans le premier cas.
Voici un exemple avec un dé: je prends un GROS dé que je lance sans le faire (trop) rouler, un peu parallèle au plan de la table (erreur de l'expérimentateur). Je m'assure de le mettre toujours dans la même position de départ dans mon expérience. Pourquoi? Je ne sais pas. Parce que cela me semble logique (encore une erreur de l'expérimentateur). Tu sens bien que la statistique dans ce contexte ne va pas se rapprocher de 1/6. Et tu vois bien que je ne peux pas en me basant sur ce résultat annoncer une probabilité.
La probabilité mathématique ce n'est pas cela. C'est le résultat d'une théorie.
Une probabilité existe en dehors d'une expérience et du résultat d'une expérience.
On peut si l'on veut valider cette théorie par des analyses statistiques mais elle n'est pas la source de la probabilité. Et d'ailleurs un résultat qui ne correspondrait pas n'infirme pas nécessairement la théorie. Il faudrait être sûr que l'expérience est valide. Je renvoie par exemple aux neutrinos super-luminiques.
#107 - 24-10-2012 09:44:12
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4050
- Lieu: hébesphénorotonde triangulaire
Et ta soeur
rivas a écrit:Par contre la probabilité n'a aucun rapport avec le fait que l'on ne maitrise pas tous les facteurs d'une expérience. C'est bien ça le problème. Faire cela c'est généraliser le constat d'une statistique et appeler cela une probabilité mais une probabilité mathématique ce n'est pas cela.
On est bien d'accord, rivas !
On ne peut pas généraliser le constat d'une statistique et appeler cela une probabilité.
Ce qui signifie qu'on ne peut pas s'appuyer sur une répartition 49% de filles à la naissance et 51% de garçons (en France) pour affirmer que la probabilité que l'autre enfant soit une fille est aux environs de 49% (j'ai arrondi volontairement les chiffres).
Et à ma connaissance, la théorie génétique dit que c'est 50-50, même si quelqu'un a affirmé que mes connaissances ne sont pas correctes. Mais comme dit Azdod, il n'y a pas d'autre théorie pour l'instant. Donc rien n'interdit de retenir 50-50.
Et en plus, tout ça dépasse le cadre d'une énigme mathématique à mon avis...
Klim.
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#108 - 24-10-2012 10:14:33
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
et ta soeue ?
Azdod a écrit:Ce sont les stats qui doivent s'approcher de la probabilité et non pas le contraire !
Ah bon ? D'où vient la valeur d'une probabilité, alors ? Elle tombe du ciel ?
Quant à ton allusion à la loi faible des grands nombres, elle est incorrecte. En effet, cette dernière indique que l'estimation statistique se rapproche de la valeur réelle quand tu augmentes la taille de ton échantillon, c'est-à-dire qu'elle ne fait appel à la notion de probabilité que dans sa définition formelle (pour pouvoir placer le fameux epsilon cher aux matheux).
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#109 - 24-10-2012 10:25:21
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Et ta seur ?
Klimrod a écrit:Ce qui signifie qu'on ne peut pas s'appuyer sur une répartition 49% de filles à la naissance et 51% de garçons (en France) pour affirmer que la probabilité que l'autre enfant soit une fille est aux environs de 49% (j'ai arrondi volontairement les chiffres).
Je suis tout-à-fait d'accord aussi.
Ce n'est pas là du tout mon point de désaccord (la valeur de la probabilité) et c'est sans doute plus juste pour le contexte de la population française du début du 21eme siecle que 50-50. Ce n'est par contre pas vrai pour la Chine par exemple.
Dans un tel cas, puisque c'est une probabilité fondée sur une statistique du fait qu'aucune théorie ne permet d'en donner une mathématique, on parle de probabilité statistique et on garde en tête qu'une incertitude et un contexte y sont associés.
C'est aussi pour cela que pour lever toute discussion, l'énoncé pourrait inclure la valeur à utiliser. Je crois que c'était le point de départ de toute cette discussion que j'ai trouvé néanmoins intéressante.
Klimrod a écrit:Et à ma connaissance, la théorie génétique dit que c'est 50-50, même si quelqu'un a affirmé que mes connaissances ne sont pas correctes. Mais comme dit Azdod, il n'y a pas d'autre théorie pour l'instant. Donc rien n'interdit de retenir 50-50.
Et en plus, tout ça dépasse le cadre d'une énigme mathématique à mon avis...
Klim.
Je ne me serais jamais permis d'affirmer une telle chose (que tes connaissances ne sont pas correctes).
J'ai cependant lu au fil du temps des éléments intéressants de nature à prouver que la théorie génétique usuelle ne traduit pas parfaitement la réalité des choses et que des théories plus pointues/sophistiquées sont en train de voir le jour et qui pourraient peut-être justement expliquer ce léger déséquilibre garço/fille.
Il faut aussi garder en tête qu'il existe d'autres associations de chromosomes sexuels que XX et XY et des genres sexuels ambigus. Voir par exemple: http://fr.wikipedia.org/wiki/Comparaiso … _l%27homme. Je ne suis donc pas du tout étonné que statistiquement on ne trouve pas 1/2 même en dehors d'une raison sociologique (sélection des males).
PS: Au sujet des liens sur wikipedia que je donne, je tiens à préciser que je n'y suis pas contributeur (à mon grand regret par manque de temps), que ce n'est donc pas une façon de faire passer ma pensée pour soutenue par d'autres en ayant écrit moi-même les articles. Je souhaite simplement ajouter des références qui me semblent valides dans un souci documentaire et d'autovérification que je ne raconte pas n'importe quoi.
#110 - 24-10-2012 10:31:56
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Et ta seur ?
MthS-MlndN a écrit:Ah bon ? D'où vient la valeur d'une probabilité, alors ? Elle tombe du ciel ?
Tu n'as as lu le thread alors ? 
Une probabilité statistique vient des statistiques.
Une probabilité vient d'une théorie.
Je redonne 2 liens très riches sur le sujet:
http://fr.wikipedia.org/wiki/Interconne … tatistique
http://fr.wikipedia.org/wiki/Statistique
D'ailleurs un sujet amusant d'énigme peut-être: comment déterminer les probabilités d'apparition des faces d'un dé non homogène, non cubique? En prenant un exemple comme 2 faces carrés reliées par 4 faces rectangulaires et de densité constante?
#111 - 24-10-2012 10:41:40
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
E tta soeur ?
rivas a écrit:Tu n'as as lu le thread alors ? 
Je dois avouer que j'en ai échappé des petits bouts...
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#112 - 24-10-2012 10:46:01
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Et ta soer ?
Je viens d'écrire un petit programme tout simple qui utilise le générateur pseudo-aléatoire de mon compilateur, qui tire des nombres entiers naturels et compte ceux divisibles par 7.
J'ai fait les tests suivants:
10^6 nombres, je trouve 142 207, 143 469, 143 261
10^7 nombres, je trouve: 1 428 489
10^8 nombres je trouve 14 284 584
Je sais très bien ce qui se passe au niveau du générateur pseudo-aléatoire et c'est pour ça que j'ai utilisé "pseudo" en tout premier lieu. Mais pour quelqu'un qui ne le sait pas parce que c'est au-delà de ses connaissances, en suivant le raisonnement de dériver la probabilité de l'expérience que peut-il en conclure?
Soit qu'une telle probabilité n'existe pas parce que la statistique varie trop. Soit tenter plus d'expériences, faire une sorte de moyenne et déclarer que c'est la probabilité (qui sera toujours aussi fausse du fait de l'implémentation du générateur de nombres pseudo-aléatoires). Dans ce cas il a établit la probabilité statistique dans son contexte et on voit bien qu'il faut nécessairement lui associer un contexte et une marge d'incertitude (sans doute l'écart-type de l'ensemble des résultats dans ce cas).
D'ailleurs quelqu'un qui utiliserait un genérateur PA plus fiable aurait d'autres résultats. Est-il possible d'avoir 2 probabilités différentes pour la même chose?
Et pourtant nous savons tous que la probabilité mathématique qu'un nombre entier naturel soit divisible par 7 est de 1/7
#113 - 24-10-2012 17:08:59
- Azdod
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 763
- Lieu: In this universe ... !!
Et ta sour ?
MthS-MlndN a écrit:Ah bon ? D'où vient la valeur d'une probabilité, alors ? Elle tombe du ciel ?
Tu penses que le 1 sur 6 d'un dé équilibré est venu des statistiques ? je doute énormément.
Par contre si je lance un dé équilibré un très grand nombre de fois, la fréquence d'apparition de chacune de ses faces va certainement converger vers le 1 sur 6.
MthS-MlndN a écrit:En effet, cette dernière indique que l'estimation statistique se rapproche de la valeur réelle quand tu augmentes la taille de ton échantillon, c'est-à-dire qu'elle ne fait appel à la notion de probabilité que dans sa définition formelle (pour pouvoir placer le fameux epsilon cher aux matheux).
Qu'est ce que tu entends par valeur réelle ? C'est sans doute la probabilité !
Bon sur cette page, on voit bien l'énoncé du théorème :
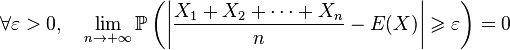
Le P signifie la probabilité sans doute !
"Zero is where everything starts ! Nothing would ever be born if we didn't depart from there"
#114 - 24-10-2012 19:42:05
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,426E+3
Et ta soeru ?
Bonsoir
Je n'ai pas lu tout le sujet mais pour les probas-stats , en 3ème on définit une probabilité comme le cas limite pour un grand nombre d'expériences . On jette une pièce deux millions de fois , elle tombe sur pile environ un million de fois , la probabilité est 1/2 . Je trouve cette approche effrayante car ce sont les chiffres avec tout ce qu'ils traînent comme imprécision , interprétation , ... , qui donnent le sens au problème et pas la logique 
Les probabiltés ( ce n'est pas ma tasse de thé ) deviennent un sous produit des stats et là ça m'affole un peu .
Faire des maths ce n'est pas compiler des chiffres mais fournir un modèle à un problème pour essayer de le résoudre .
Bref ce problème n'a pas de sens parce qu'on dit pas de quoi on parle , on met des chiffres en parallèle on ne sait pas pourquoi !!!
Vasimolo
#115 - 25-10-2012 09:11:16
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4050
- Lieu: hébesphénorotonde triangulaire
Et ta oseur ?
vasimolo a écrit:Faire des maths ce n'est pas compiler des chiffres mais fournir un modèle à un problème pour essayer de le résoudre

J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#116 - 25-10-2012 09:53:14
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
Et ta seur ?
@Vasimolo: Je ne saurais être plus en accord avec toi 
#117 - 25-10-2012 14:01:43
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
et ta sozur ?
1) Le sens/L'interprétation d'une probabilité (pas sa définition en tant qu'objet mathématique, la théorie des Probas n'a pas besoin de celle des Stats) est souvent donné par les Stats : on parle de répétition d'expérience, de fréquence limite et donc de Stats.
Selon moi, cette interprétation se heurte toujours à l'écueil de la traduction de l'infini mathématique ou bien à ce que le serpent se morde la queue quelque part (il est question de proba pour interpréter une proba...). Mais franchement, je n'ai pas de meilleure explication pour un néophyte. Vasimolo, qu'est-ce que tu proposes sans recourir aux Stats, ça m'intéresse ?
2) Est-ce que pour justifier le 1/6 on est obligé de lancer le dé plein de fois et de faire une moyenne ? Non. Ici les arguments pour l'équiprobabilité sont le fait que le dé est un cube (entre autres ces faces sont identiques) que l'on suppose parfait et homogène. On donne des arguments pour l'équiprobabilité. Elle ne tombe pas du ciel, ni des stats. Bon, il faut voir que le dé équilibré reste un modèle puisqu'en vrai, le dé ne sera pas parfait. C'est la même chose pour le pile ou face, le tirage de boules identiques dans une urne, le tirage de cartes, etc... où l'on présente des arguments en faveur de l'équiprobabilité. La reproduction humaine est un phénomène bien plus compliqué qu'un lancer de dé. Quels sont les arguments en faveur de l'équiprobabilité d'être une fille ou un garçon ? Le fait que le chromosome Y soit beaucoup plus long que le X ? Hou là, ça m'a l'air mal parti...
3) Les intervalles de fluctuations : Lorsqu'on répète n fois une expérience, on sait que la fréquence d'apparition d'une issue va fluctuer autour de sa proba. Et pas n'importe comment (je ne vais pas détailler plus que ça ici). Ceci permet d'invalider des modélisations à partir des stats fournies pour un n suffisamment grand. Par exemple si quelqu'un vient me dire qu'à la naissance, un individu a une chance sur 2 d'être une fille, je peux rejeter son modèle en lui présentant les stats de l'INED (en étant presque sûr de ne pas me tromper).
4) Les intervalles de confiance : cela permet d'estimer une proportion et pourquoi pas de mettre en place un modèle probabiliste à partir de stats, tout en contrôlant l'imprécision. Si j'ai les groupes sanguins d'une part suffisamment grande d'une population génétiquement homogène, je vais pouvoir extrapoler à l'ensemble de la population et pourquoi pas modéliser une expérience aléatoire portant sur le groupe sanguin d'un individu pris au hasard dans cette population.
#118 - 25-10-2012 17:06:24
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
Et ta soeuur ?
Je ne suis pas d'accord avec le fait qu'un dé parfait n'existe pas. Physiquement, il est tout à fait possible qu'il soit fabriqué de telle sorte que les imperfections/hétérogénéités (le mot français qui compte le plus de é), ou plutôt les dégénérescences (le mot français qui compte le plus de e, avec ou sans accent) soient négligeables.
Et pis même si vous êtes pas d'accord, c'est pareil !
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#119 - 25-10-2012 17:38:28
- rivas
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1106
- Lieu: Jacou
et ta soeir ?
Vous allez voir qu'on va finir par être tous d'accord 
#120 - 29-06-2013 23:59:02
- Origine
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 16
et ta soeyr ?
C'est simple, la probabilité est de 2/3, car on élimine le cas FF, puisqu'il dit être un garçon !
#121 - 30-06-2013 00:06:18
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
et ta speur ?
Oh dare! En voilà un qui veut relancer le débat 
Intéressant soit dit en passant, je ne verrai plus les probabilités comme avant 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#122 - 30-06-2013 01:42:32
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Et ta soeu ?
Tiens j'avais loupé cette discussion. Bon ben je vais y apporter ma modeste contribution, car j'adore les probas. On va repartir pour 4 pages 
Titoufred, si on veut raisonner en bon biologiste, alors à moins de faire tourner un modèle de fou, il faudrait connaître les âges respectifs du frère et de l'autre "enfant". Pourquoi ?
Information n°1: tu es en âge de poser la question "quelle est la probabilité que j'aie une sœur". Tu n'es donc pas un nouveau-né et tu as au minimum 5 ans. Si tu parles de probabilité, mettons même que tu en aies au moins 10 (mais tu peux aussi très bien en avoir 70). Donc, le sex-ratio à la naissance n'est pas l'élément à prendre en compte puisque après s'effectue un biais correctif de survie post-naissance: en France, il y a plus de femmes que d'hommes alors qu'il naît plus de garçons que de filles.
Information n°2: ta question est en français. Donc, le garçon vit en Francophonie. Mais en Europe ou en Afrique ?
Le problème est donc que la réponse à cette question va dépendre:
- des âges respectifs du frère et de l'autre enfant
- du sex-ratio instantané à ces âges respectifs
- et donc du pays puisque le sex-ratio instantané diffère selon les pays
#123 - 30-06-2013 08:02:28
- Origine
- Habitué de Prise2Tete
- Enigmes résolues : 0
- Messages : 16
t ta soeur ?
Le problème ici, c'est que l'on ne sait pas quelle place il occupe dans l'ordre. En effet, ici, on a une analyse combinatoire ordonnée. Si la question avait été: "Je suis issu d'une famille de deux enfants, je suis né le premier. Quelle est la probabilité que l'autre enfant soit une fille? Note: On considère la probabilité d'avoir un garçon de 1/2 et on se balance des marges d'erreurs."
Là, nous aurions 1/2, car cela serait soit GF ou GG. Ce qui change la donne c'est que nous ne savons pas s'il est le premier ou le deuxième, mais nous savons qu'il y a un garçon.
C'est pour cela qu'il y a 2 chances sur 3 que l'autre enfant soit une fille.
P.S. à celui qui parlait de la francophonie et qui A EXCLU LE QUÉBEC ! INACCEPTABLE ! TU N'ES QU'UN NOMBRILISTE ! Bon d'accord, je suis québécois. On se fait souvent oublier de l'autre côté de l'océan à vivre au-dessus de gens qui sont principalement au-dessus de leur poids-santé (au cas où vous n'auriez pas compris, je parle des américains).
P.P.S Je dois cependant avouer que ton point est intéressant. Puisqu'il pose la question en français, c'est qu'il vient soit du Québec, soit de l'Afrique, mais tu n'as pas pensé qu'il puisse être bilingue aussi ou encore issu d'une famille d'immigrants. Cela augmente le spectre des recherches. Mais bon, bien qu'il soit intéressant de trouver où se situe sa maison (ou son appartement), cela ne semble pas si pertinent pour résoudre l'énigme vu le manque total d'infos que nous avons sur ce problème.
#124 - 30-06-2013 09:46:21
- Nombrilist
- Expert de Prise2Tete
- Enigmes résolues : 10
- Messages : 568
Et t asoeur ?
Ah oui, comment ai-je pu oublier nos amis québécois ? Mille excuses. En fait ici, mon intervention a pour but de ramener un peu de réalité biologique dans le débat. Ce fil n'est pas tellement dédié à la résolution du problème (on sait tous que la réponse théorique est 2/3), mais plus à la façon d'appréhender la probabilité "p" d'avoir un garçon ou une fille.
Nous avons tous postulé p = 0.5 alors que Titou objecte que le ratio garçon/fille à la naissance n'est pas de 1/1. Et donc on ne peut pas avoir p=0.5
Il a raison. Mais à ce moment-là, si on veut vraiment prendre un "p" réaliste, il faut tenir compte des paramètres que j'ai listé ci-dessus, et non du sex-ratio à la naissance qui n'a aucun intérêt pour ce problème. Il en aurait si il avait dit "que j'aie ou aie eu une soeur". Le fait que l'autre enfant soit en vie est le noeud du problème. Désolé pour lui ^^.
"cela ne semble pas si pertinent pour résoudre l'énigme vu le manque total d'infos que nous avons sur ce problème."
Justement, l'idée était d'aller à la pêche aux infos pour donner une solution plus approchée du problème que le théorique 2/3
#125 - 30-06-2013 09:57:04
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Et ta seour ?
Tout à fait d'accord avec les remarques de Nombrilist.
Mais sinon, relisez le début du fil, on navigue autour de 1/2 et pas 2/3 !
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum