|
#1 - 06-01-2013 12:09:00
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
pliage eépétitif vers la droite !
Bonjour, bonne année 
En cette nouvelle année, voici une petite recherche mathématiques rigolote.
Imaginons que nous plions une feuille en deux vers la droite puis que nous regardons la forme obtenue une fois relâchée nous obtenons une figure. Nous répétons cette opération c'est à dire on plie toujours vers la droite.
Evidemment en pratique au bout du 3ème ou 4ème pliage, il nous serait impossible de continuer mais dans notre monde théorique des maths on va supposer que l'on peut continuer ainsi à l'infini.
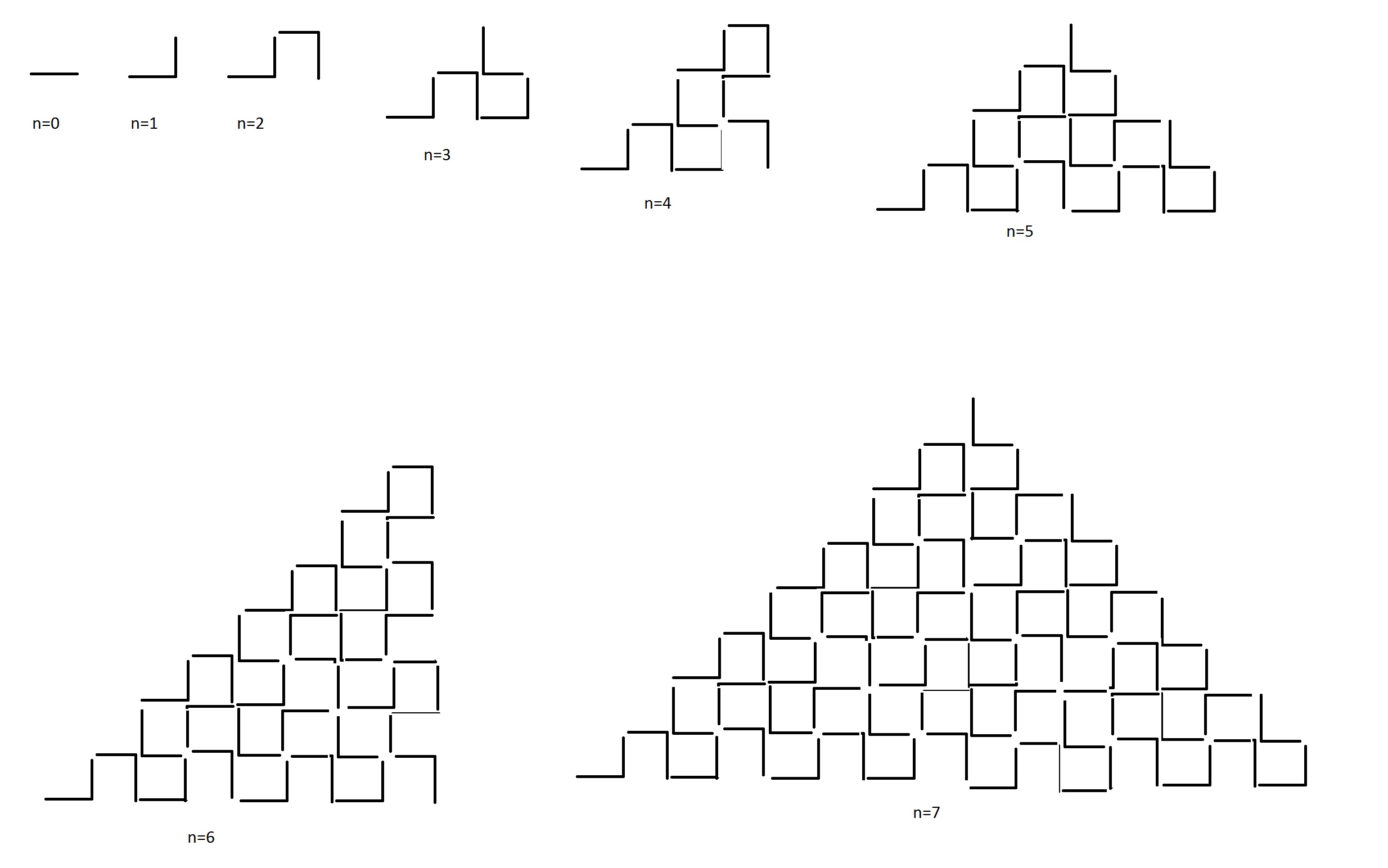
Sur le dessin ci dessous je vous ai présenter les premières étapes.
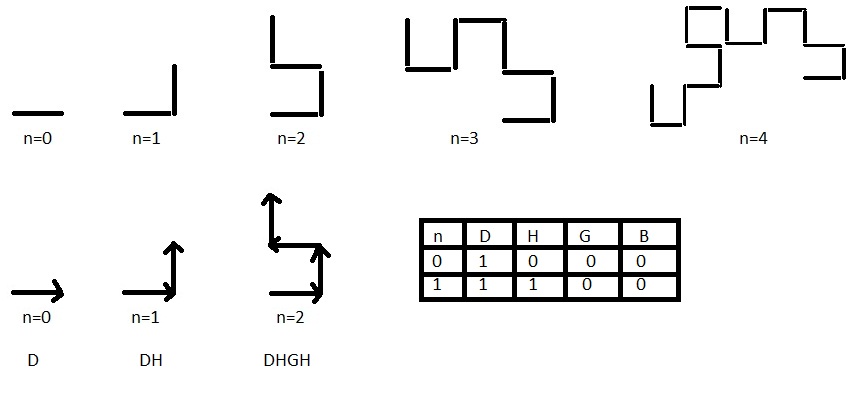
http://www.prise2tete.fr/upload/gilles355-mathej.jpg
J'ai fléché le parcours, on obtient donc à l'étape 0 ( quand on n'a pas encore plié la feuille ) une flèche vers la droite, pour l'étape 1, une flèche vers la droite et une vers le haut etc.
Ma première question est pouvez vous me dire combien y aura t-il de flèches vers la droite, le haut, la gauche et le bas au bout du 8ème pliage.
Réponse à valider dans la case réponse sous le format DxxHyyGzzBww où xx est le nombre de flèches à droite, yy le nombre de flèche vers le haut etc.
La deuxième question est pouvez vous me donner une formule ou explication pour le nième pliage ?
Enfin pour ceux qui aiment les jolis dessins, pouvez vous me représenter la forme des pliages si on alterne un pliage vers la droite puis un vers la gauche etc.
Voilà amusez vous bien et n'hésitez pas à me poser des questions 
#2 - 06-01-2013 12:21:07
- SHTF47
- Imprnnçbl de Prs2Tt
- Enigmes résolues : 39
- Messages : 1629
- Lieu: Autre nom du colin
Pliage répétiti vers la droite !
A force de plier vers la droite (et en supposant que c'est toujours possible physiquement bien sûr), on finit par obtenir ceci, je pense :

 Plus sérieusement, ce petit pliage innocent est connu, et il permet la construction "à la main" d'une fractale : la courbe du dragon Plus sérieusement, ce petit pliage innocent est connu, et il permet la construction "à la main" d'une fractale : la courbe du dragon
Je suis conscient que ça ne répond pas vraiment aux questions que tu poses... mais j'ai pas envie de compter des flèches en fait... c'est dimanche hein !!!
Et pour ce qui est du pliage "une fois à droite, puis une fois à gauche", j'ai pas encore cherché, mais j'imagine qu'on va trouver quelquechose de joli.
A suivre
La musique est une mathématique sonore, la mathématique une musique silencieuse. [Edouard HERRIOT]
#3 - 06-01-2013 13:17:55
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
Pliage répétitif vesr la droite !
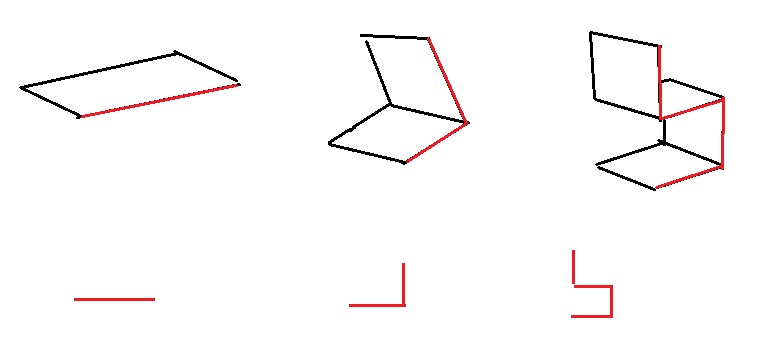
Ca devrait pas faire un carré au deuxième pliage parce que si je suis la logique ça donne ça. Peut-être que je me trompe ... (ou plutôt c sur)
#4 - 06-01-2013 13:40:55
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,192E+3
pliage répétitif vers la droire !
Je ne comprends rien à l'énoncé... 
Si on plie une feuille toujours en deux vers la droite, ça fait juste des lignes verticales parallèles non ?
EDIT : je viens de comprendre, tu représentes la feuille vue par la tranche !
Je tombe sur D67 H62 G61 B66 non validé.
#5 - 06-01-2013 16:27:56
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Pliage répétitf vers la droite !
J'ai rien compris dès le départ.
Pourrais tu préciser ce qu'est le pliage vers la droite, et quelle figure on obtient ?
1 pli= 1 trait (au milieu, vertical, horizontal ?) et rabattre l'un des cotés sur l'autre. La figure obtenue, c'est vu de face ou de profil ? Rabattre un coté, c'est à 180° ?
Une fois que tu auras précisé tout ça, peut être ça devrait être plus clair, pour moi en tout cas.
merci d'avance.
#6 - 06-01-2013 18:15:43
- JulesV
- Passionné de Prise2Tete
- Enigmes résolues : 15
- Messages : 52
pliage répétitif vers la droire !
On peut trouver une technique récursive. Il suffit de voir que D et H dans DH qui représente un pliage peuvent être remplacés par un motifs constitué de plusieurs flèches, avec le motif restitué pour D et ayant subi une rotation dans le sens direct de 90 degré pour H.
Par exemple du motif [latex]m_2[/latex] : DHGH on déduit la première moitié du motif [latex]m_3[/latex]: DHGH|****. On construit avec les règles de rotations la deuxième moitié du motif [latex]m_3 [/latex](D transformé en H, H en G, G en B, B en D )
On a ainsi [latex]m_3[/latex]: DHGH|GBGH (la symétrie s'explique du fait qu'une rotation commence par le "bout")
On peut trouver de la même façon la représentation graphique de [latex]m_8[/latex] (que je n'ai pas trouvé, pas envie de me casser la tête avec 256 caractères  ) )
Pour trouver la formule générale, il faut voir comment sont définies les suites [latex](D_n), (G_n), (H_n) [/latex] et [latex](B_n)[/latex]
On a [latex] D_0=1, G_0=0, H_0=0, B_0=0[/latex]
et
[TeX]D_n=D_{n-1}+B_{n-1}[/TeX][TeX]H_n=H_{n-1}+D_{n-1}[/TeX][TeX]G_n=G_{n-1}+H_{n-1}[/TeX][TeX]B_n=B_{n-1}+G_{n-1}[/TeX]
On en déduit (je l'ai vu avec un tableau  ) que les suites prennent les valeurs des termes du tableau de Pascal tronqué et donc cyclique à un moment (en s"alignant avec le numéro des motifs: ) que les suites prennent les valeurs des termes du tableau de Pascal tronqué et donc cyclique à un moment (en s"alignant avec le numéro des motifs:
Soit
[TeX]D_n= \sum_{i=0}^{ceil(\frac{n+1}{4} )} {n \choose 4k} [/TeX][TeX]H_n= \sum_{i=0}^{ceil(\frac{n}{4} )} {n \choose 4k+1} [/TeX][TeX]G_n= \sum_{i=0}^{ceil(\frac{n-1}{4} } {n \choose 4k+2} [/TeX][TeX]B_n= \sum_{i=0}^{ceil(\frac{n-2}{4} )} {n \choose 4k+3} [/TeX]
ceil(n) retourne l'entier supérieur du nombre n. ceil(4,5)=ceil(4,314)=5 par exemple.
Pfiuuu.... 
Edit
@Gilles : J'ai bien D72H64G56B64 avec
D=C(8,0)+C(8,4)+C(8,8)=72
H=C(8,1)+C(8,5)=64
G=C(8,2)+C(8,6)=56
B=C(8,3)+C(8,7)=64
mais je trouve ce résultat indépendamment, je me suis un peu précipité pour la formule, il faut que je me relise car je me suis un peu emmêlé les pinceaux avec les lignes, le rang l'indice, les arrangements... 
#7 - 06-01-2013 18:27:09
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Pliiage répétitif vers la droite !
Soient D(n), H(n), G(n) et B(n) le nombre de flèches respectives vers la droite, le haut, la gauche et le bas, pour l'étape n. On aura les relations:
D(n+1)=D(n)+B(n); H(n+1)=H(n)+D(n); G(n+1)=G(n)+H(n) et B(n+1)=B(n)+G(n).
A l'étape 8, cela donne D72H64G56B64, validé par la case réponse.
J'ai dessiné les formes des pliages en les alternant vers la droite et vers la gauche, mais je ne peux pas les faire partager ici car je ne sais pas dessiner sur ce site.
On peut remarquer que: D(n)+H(n)+G(n)+B(n)=2^n.
Je cherche une expression plus simple pour D(n), H(n), G(n) et B(n) et je reviendrai plus tard.
Merci pour cet exercice ludique.
#9 - 06-01-2013 18:53:23
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
PPliage répétitif vers la droite !
Pour l'instant le seul à avoir validé la case réponse est Franky1103, pour JulesV je ne suis pas sûr ... j'attends que tu valides ma première question et je regarderai plus précisément ta formule.
Edit: @ JulesV je pense que c'est pas mal du tout en fait ta formule.
#10 - 06-01-2013 20:28:13
- FRiZMOUT
- Verbicruciste binairien
- Enigmes résolues : 49
- Messages : 2218
pliage répétitig vers la droite !
D72H64G56B64
avec [latex]P_n = \{D_n , H_n , G_n , B_n\}[/latex] :
[TeX]P_0 = \{1 , 0 , 0 , 0\}[/TeX]
[TeX]P_{n+1} = \{D_n + B_n, H_n + D_n, G_n + H_n, B_n+ G_n\}[/TeX]
#11 - 06-01-2013 21:01:34
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
Pliage répétiti vers la droite !
J'ai plein de bonne réponse pour la première question, pour la seconde j'ai de la récurrence mais le seul pour l'instant à avoir donné une formule en fonction de n est JulesV
Personne ne s'est attaqué au dessin un coup à droite un coup à gauche.
#12 - 07-01-2013 10:37:47
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Pliage répétitif vers la drroite !
Voici les valeurs de D(n); H(n); G(n) et B(n) suivant la valeur de n modulo 4:
Si n=0 (modulo 4), alors:
H(n)=B(n)=2^(n-2)
D(n)=2^[(n-2)/2].{2^[(n-2)/2]+(-1)^(n/4)}
G(n)=2^[(n-2)/2].{2^[(n-2)/2]-(-1)^(n/4)}
Si n=1 (modulo 4), alors:
D(n)=H(n)=2^[(n-3)/2].{2^[(n-1)/2]+(-1)^[(n-1)/4]}
G(n)=B(n)=2^[(n-3)/2].{2^[(n-1)/2]-(-1)^[(n-1)/4]}
Si n=2 (modulo 4), alors:
D(n)=G(n)=2^(n-2)
H(n)=2^[(n-2)/2].{2^[(n-2)/2]+(-1)^[(n-2)/4]}
B(n)=2^[(n-2)/2].{2^[(n-2)/2]-(-1)^[(n-2)/4]}
Si n=3 (modulo 4), alors:
D(n)=B(n)=2^[(n-3)/2].{2^[(n-1)/2]+(-1)^[(n+1)/4]}
H(n)=G(n)=2^[(n-3)/2].{2^[(n-1)/2]-(-1)^[(n+1)/4]}
Y a t-il une expression plus simple ?
#13 - 07-01-2013 20:27:48
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
oliage répétitif vers la droite !
Je crois que c'est plus rigolo de débattre plutot que de chercher seul dans son coin.
Je vous prépare le pliage alterné pour bientot 
#14 - 07-01-2013 21:51:14
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Pliage répétitif vers la droit !
toujours pas compris le coup du plis toujours à droite. Pourquoi cela ne donne-t-il pas un carré sur lequel on s'enroule ?
#15 - 07-01-2013 23:03:18
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
Pliage réptéitif vers la droite !
@golgot59:
On plie la bande de papier en deux, puis à nouveau en deux (on a quatre épaisseurs), puis encore en deux (on a huit épaisseurs), etc. On ne "roule" pas la bande de papier sur elle-même. Quand on la déplie, les plis sont parfois à droite et parfois à gauche.
#16 - 07-01-2013 23:27:21
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
pliage répéritif vers la droite !
Ca y est, compris !
J'avais pas compris qu'il fallait plier complètement le papier pour ensuite le déplier "à moitié"  (désolé) (désolé)
#17 - 08-01-2013 06:12:07
- nodgim
- Elite de Prise2Tete
- Enigmes résolues : 0
- Messages : 3839
Pliage répétitif vers la droitee !
Ah ouais, pareil, j'avais pas compris depuis le début. Dommage.
#18 - 09-01-2013 21:42:30
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
pliage eépétitif vers la droite !
Ah ok, c pour ça que ça ne fais pas un carré !!!
Ok, trop compliqué pour moi ...
#19 - 10-01-2013 10:11:35
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum