Bonjour,
Ce site n'est pas un site d'aide aux devoirs.

Bon, je sors...

Une réponse

Notons:
longueur du cote AB = c et l'angle opposé A
longueur du cote AC = b et l'angle opposé B
longueur du cote BC = a et l'angle opposé C
la hauteur relative au côté BC est noté AO=h où O est le projeté orthogonal de A sur (BC)
Soient les distances x=OC et y=OB (on remarquera que a=x+y ou y=a+x selon le triangle ayant un angle inconnu obtus ou non). Pour la suite, j'adopte a=x+y

Les théorèmes de bas:
[TeX]S=\frac{1}{2}*b*c*sin(A)  (1)[/latex] (théorème des sinus),
[latex]S=\frac{h*a}{2}[/latex] soit [latex]h=\frac{2*S}{a}  (2)[/latex] (calcul classique),
[latex]a^2=b^2+c^2-2*b*c*cos(A)  (3)[/latex] (théorème d'Al-Kashi).

Résolution :
En tirant de (1) l'expression de b*c et en introduisant cette expression dans (2) on a: [latex]a^2=b^2+c^2-\frac{4*S}{tan(A)}  (4)[/TeX]
Remarquons que les triangles ABO et ACO sont rectangles en O et donc d'après Pythagore: [latex]b^2=h^2+x^2 [/latex] et  [latex]c^2=h^2+y^2 [/latex] avec [latex]y = a-x[/latex],

Les expressions précédentes de [latex]b^2  et  c^2 [/latex] introduites dans (4) donnent:
[TeX]a^2=h^2+x^2+h^2+(a-x)^2-\frac{4*S}{tan(A)}  (5)[/TeX]
Tout développement et simplification bien faits (j'espère les avoir bien faits ), on a: [latex]x^2-a*x+h^2-\frac{2*S}{tan(A)}  (5)[/latex]
Nous avons une équation de 2nd degré à résoudre, son déterminant est :
[TeX]D=a^2-4*h^2+\frac{8*S}{tan(A)}=a^2-\frac{16*S^2}{a^2}+\frac{8*S}{tan(A)}[/latex].

Normalement D devrait être positif sauf pour un triangle extraterrestre

[latex]x=\frac{a+\sqrt{D}}{2}[/latex]. Si on avait pris y=a+x, on aurait [latex]x=\frac{-a+\sqrt{D}}{2}[/TeX]
Après le calcul de x selon l'une de ces formules, on peut tomber  sur une anomalie: x<0 (x est censé être une distance et donc positif) mais cela veut juste dire qu'un des angles du triangle en question est obtus. Vous l'aurez compris, x=0 pour une triangle rectangle.

Les formules recherchées:
[TeX]AC=b=\sqrt{h^2+x^2}[/TeX][TeX]AB=c=\sqrt{h^2+(a-x)^2}[/TeX]
L'angle opposé à AC: [latex] B = arsin(\frac{2*S}{a*c})[/latex]

L'angle opposé à AB: [latex] C = arsin(\frac{2*S}{a*b})[/latex]

avec pour rappel [latex]x=\frac{a+\sqrt{D}}{2} [/latex] ;  [latex]h=\frac{2*S}{a}[/latex] et [latex]D=a^2-\frac{16*S^2}{a^2}+\frac{8*S}{tan(A)}[/latex]

Il y a peut-être des méthodes moins longues mais voilà la mienne

Intéressant.
Ce n'est pas impossible. La beauté avec un triangle c'est que 3 données indépendantes définissent toujours le triangle de façon unique.
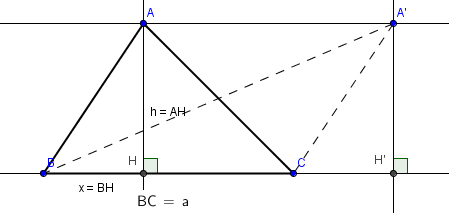
Ici, la surface et un côté étant donnés, on peut déterminer la hauteur puisque [latex]S=\dfrac{ah}2[/latex]. On sait donc que le troisième sommet se trouve sur une parallèle à (BC) située à une distance h de (BC). Puisque l'angle au point A est connu, le triangle est déterminé à 2 symétries près (le choix du côté par rapport à BC et le choix par rapport à la médiatrice de [BC].

Voyons maintenant comment trouver quelques formules.
J'ai trouvé 2 méthodes pour arriver au but mais aucune ne donne de formule très simple...

J'utilise les notations classiques suivantes:
AB=c, BC=a (connu), AC=b.

Méthode 1:
[TeX]S=\dfrac{bc sin Â}{2} [/latex] (Produit vectoriel) [latex]\Rightarrow c=\dfrac{2S}{b sin Â}[/latex] (1)

[latex]a^2=b^2+c^2-2bc.cosÂ[/latex] (Al-Kashi)

D'où: [latex]a^2=b^2+\dfrac{4S^2}{b^2 sin^2 A} [/latex] [latex]-2b\dfrac{2S cosA}{b sin A}[/TeX]
Finalement:  [latex]b^4-(a^2+\dfrac{4S}{tanA})b^2+\dfrac{4S^2}{sin^2A}=0[/latex]

C'est une équation de degré 2 en [latex]b^2[/latex] que l'on peut résoudre sans grande difficulté mais avec quelques calculs. On calcule le discriminant (je vous laisse simplifier le calcul):
[TeX]\Delta=a^4-16S^2+\dfrac{8Sa^2}{tanA}[/TeX]
Cela permet de calculer b^2 puis b puis c avec la formule (1) ci-dessus.
Il est même possible que c^2 soit la seconde solution de l'équation.

Pour trouver les 2 autres angles, on utilise:
[TeX]\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}[/TeX]
Méthode 2 (plus géométrique):

Les formules ci-dessous sont vraies si A est "au-dessus" de BC. Je traite plus bas le cas ou A n'est pas au-dessus de BC.
[TeX]Â=arctan\dfrac{x}{h}+arctan\dfrac{a-x}{h}[/latex] (2)

En utilisant la formule [latex]tan(a+b)=\dfrac{tana+tanb}{1-tana.tanb}[/latex], on trouve:

[latex]tanA=\dfrac{\dfrac{x}h+\dfrac{a-x}h}{1-\dfrac{x(a-x)}{h^2}}=\dfrac{ah}{h^2-x(a-x)}[/TeX]
D'où (en utilisant [latex]h=\dfrac{2S}{a}[/latex]): [latex]x^2-ax+\dfrac{4S}{a^2}-\dfrac{2S}{tanA}=0[/latex] (3)

Equation de degré 2 en x dont le discriminant est:
[TeX]\Delta=a^2-4(\dfrac{4S^2}{a^2}-\dfrac{2S}{tanA})=a^2+\dfrac{8S}{tanA}-\dfrac{16S^2}{a^2}[/latex].

C'est exactement le discriminant de la méthode 1 divisé par [latex]a^2[/latex] (ce qui me semble normal).

A partir de là on trouve x (les 2 solutions étant les symétries par rapport à la médiatrice de BC).

Puis les angles B et C grâce à: [latex]tanB=\dfrac{h}x[/latex] et [latex]tanC=\dfrac{h}{a-x}[/latex], puis les longueurs b et c grâce à:
[latex]\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}[/TeX]
Finalement si A n'est pas au-dessus de BC mais par exemple à droite, la formule (2) devient:
[TeX]Â=arctan\dfrac{x}{h}-arctan\dfrac{x-a}{h}[/TeX]
Or arctan étant impaire, cela donne exactement la même formule que (2) et donc les mêmes solutions.

Voila, ce n'est pas exactement les formules demandées qui se trouve sans difficulté à partir de ces méthodes mais elles sont un peu lourdes à écrire.
Merci pour cet exercice intéressant et différent.
J'attends avec curiosité de voir si quelqu'un trouvera des formules plus simples.

J'ai l'impression que résoudre ce problème revient à se demander : " A quelle distance de B la hauteur issue de A coupe [BC]."

Je crois devoir chercher dans les formules de premières S, les relations des sinus, de l'aire, formule de héron.

Je n'ai pas trouvé d'autre moyen que de le faire analytiquement.

Soit mon triangle ABC.

J'utilise le repère orthonormal (A; AB->/AB; j->). Je pose AB=l et Angle A=@

Je connais l'aire de mon triangle, je peux donc calculer la hauteur h relative au côté [AB] de mon triangle : h=Aire/l.

J'obtiens : A(0;0); B(l; 0); C(x;h) où seul x est inconnu.
->  ->
CA.CB=-x*(l-x)+(-h)*(-h)=x²-lx+h², et
->  ->
CA.CB=CA.CB.cos@=√(x²+h²)*√((x-l)²+h²)*cos@

Si j'ai le temps, j'essayerai de voir si ça se simplifie, mais ça nous donne au moins une équation du 4ème degré en x qui devrait avoir 4 solutions réelles puisqu'il existe 4 position possibles au points C (par symétrie).

Eh bien on ne peut pas appliquer Al-Kashi?
Après je pense qu'il y a une infinité de solutions donc ta demande concerne le rapport entre les deux côtés peut-être? Sinon je ne vois pas ce que tu demandes.

Bravo Rivas et kossi_tg !

Bonjour,

Nous avons bien les mêmes formules (j'ai un [latex]a^2[/latex] sous la racine imbriquée en plus qui vient du a que tu as devant cette même racine).

As-tu essayer de calculer [latex]AB.AC [/latex] ou plutôt [latex]AB^2.AC^2[/latex]. Tu devrais trouver [latex]\dfrac{4S^2}{sin^2A}[/latex] puisque c'est de là que je suis parti et c'est aussi à ça que tu veux arriver.

En regardant [latex]AB^2.AC^2[/latex] tu vois la forme [latex](x-y)(x+y)[/latex] à mettre en [latex]x^2-y^2[/latex] ce qui devrait te permettre d'éliminer toutes les racines et en utilisant [latex]sin^2A=1-cos^2A=\dfrac{tan^2A}{1+tan^2A}[/latex] tu devrais y arriver.

Tiens-nous au courant.

On n'en pense pas non plus