Enigme Combien de lancers de dé avant de... ? 5/6 @ Prise2Tete

godisdead · #101

Post 37 :Quelle est ton espérance de gain ?

post 89) tu ne réponds pas à la question.
Si je reprends ton tableau pile ou face :
On voit qu'après 2 jets.
Les deux joueurs ont autant de chance de gagner !
Après 3 jets. Tu as 8 sequences favorables au 65, pour seulement 6 au 66.

Donc en moyenne, le 65 gagnera plus souvent que le 66 !

PRINCELEROI · #102

post 89
Mais non

sur les 16 cas 8 sont morts.

il en reste 8 et c'est 2 à 2

Le premier qui y arrive a gagné la partie.

post 37 je pense 10/9

godisdead · #103

Je te reponds ce soir (faut un peu bosser de temps en temps )

godisdead · #104

Reprenons l'exercice. Deux joueurs lancent 3 fois la pièce.
Si le premier joueur fait PP en premier, il gagne.
Si le deuxième joueur fait PF en premier, il gagne. Sinon, match nul.
Cela ne répond pas à 100% à la problématique, mais je pense que c'est largement suffisant pour démontrer la faille dans la logique de princeleroi.
Nous avons donc 64 parties différentes possibles !

Joueur 1 Joueur 2 Gagnant
P P P | P P P | J1
P P F | P P P | J1
P F P | P P P | N
P F F | P P P | N
F P P | P P P | J1
F P F | P P P | N
F F P | P P P | N
F F F | P P P | N
P P P | P P F | J1
P P F | P P F | J1
P F P | P P F | J2
P F F | P P F | J2
F P P | P P F | N
F P F | P P F | J2
F F P | P P F | J2
F F F | P P F | J2
P P P | P F P | N
P P F | P F P | N
P F P | P F P | J2
P F F | P F P | J2
F P P | P F P | J2
F P F | P F P | J2
F F P | P F P | J2
F F F | P F P | J2
P P P | P F F | N
P P F | P F F | N
P F P | P F F | J2
P F F | P F F | J2
F P P | P F F | J2
F P F | P F F | J2
F F P | P F F | J2
F F F | P F F | J2
P P P | F P P | J1
P P F | F P P | J1
P F P | F P P | N
P F F | F P P | N
F P P | F P P | J1
F P F | F P P | N
F F P | F P P | N
F F F | F P P | N
P P P | F P F | J1
P P F | F P F | J1
P F P | F P F | J2
P F F | F P F | J2
F P P | F P F | N
F P F | F P F | J2
F F P | F P F | J2
F F F | F P F | J2
P P P | F F P | J1
P P F | F F P | J1
P F P | F F P | N
P F F | F F P | N
F P P | F F P | J1
F P F | F F P | N
F F P | F F P | N
F F F | F F P | N
P P P | F F F | J1
P P F | F F F | J1
P F P | F F F | N
P F F | F F F | N
F P P | F F F | J1
F P F | F F F | N
F F P | F F F | N
F F F | F F F | N

Le joueur 1 (PP ou 66) gagne 16 fois
Match nul 26 fois
Le joueur 2 (PF ou 65) gagne 22 fois

PRINCELEROI · #105

Je ne comprend pas ton tableau.
Mais si tu veux un paradoxe: sur deux lancers je choisis PP si tu prends FP tu gagnes dans 75% des cas,pourtant, il sont équiprobables.

godisdead · #106

Mais si tu veux un paradoxe: sur deux lancers je choisis PP si tu prends FP tu gagnes dans 75% des cas,pourtant, il sont équiprobables. ?

Tu peux me le démontrer ?

Mon tableau est simple, sur 3 lancers, il donne toutes les parties différentes possibles et la dernière colonne détermine le vainqueur !

PRINCELEROI · #107

Pour le paradoxe:si pile sort il te faut un deuxième pile pour gagner,si un face sort au premier jet ou au deuxième je gagne dans tous les cas.
Pour ton tableau désolé mais je ne le comprend pas.

godisdead · #108

Encore une fois, tu ne comprends pas l'énoncé !
Il n'y a un dé/pièce pour les deux joueurs, mais un chacun !

Donc si le premier joueur joueur sort FFFPP
Et le deuxième sort PFFFF
Le premier joueur gagne (à ton jeu bien entendu)

Le FP sorti par le premier joueur ne fait pas gagner le deuxième !

Et encore une fois, sur une succession de jet (et non, le jet simultané de 2 dés/pièces), FP arrivera avant PP !

Pour en revenir à mon tableau, pour 3 lancers de pièces, chaque joueur à 8 enchaînements possibles !
Jusque là, es-tu d'accord ?
Donc, il existe 8*8, 64 jeux différents possibles, d'accord ?
Sur ces 64 jeux, le J2 gagne plus souvent que le joueur 1, d'accord ?

PRINCELEROI · #109

oups

Il n'y a pas un dé/pièce pour les deux joueurs, mais un chacun !

tu as raison désolé.

titoufred · #110

Personne n'a encore répondu aux questions complémentaires sur le cas général.

Par exemple, parmi les 5 combinaisons "654", "665", "566", "656" et "666", lesquelles nécessitent plus de lancers que les autres en moyenne pour apparaître ?

Combien de lancers faut-il en moyenne pour voir apparaître chacune de ces 5 combinaisons ?

Il y a plein d'indices tout au long du sujet...

titoufred · #111

Tiens, la théorie oscillatoire de kossi_tg/Mathias pour l'énigme "Promenons nous dans le train" peut s'adapter pour répondre facilement aux questions posées dans ce sujet. Qui est-ce qui voit comment ?

kossi_tg · #112

Je vois que ma théorie peut avoir de l'avenir lool:

D'après l'explication émise par Mathias: si 1 chance sur k de réaliser une chose, je la réaliserai en moyenne toutes les n fois.

Revenons à ma suite [latex](U_n)[/latex]:
- avoir un 6: 1 chance sur 6: [latex]U_1=6[/latex],
- avoir 2 six de suite: 1 chance sur 36: [latex]U_2=36[/latex],
....
- avoir n six de suite: 1 chance sur [latex]6^n[/latex]: [latex]U_n=6^n[/latex].

On remarque que [latex](U_n)[/latex] est une suite géométrique de raison 6 et de premier terme [latex]U_1=6[/latex].

Le nombre moyen de lancers pour obtenir n six de suite est la somme des n premiers éléments de [latex](U_n)[/latex]
[TeX]LancersMoyens(n)=\sum_{i=1}^{n}U_i=U_1*\frac{6^n-1}{6-1}=\frac{6}{5}*(6^n-1)[/TeX]
CQFD

titoufred · #113

Je ne comprends pas très bien à quoi correspondent les [latex]U_i[/latex] dans ton raisonnement et pourquoi tu en fais la somme.

kossi_tg · #114

[latex]U_i[/latex] est l'inverse de la probabilité d'avoir [latex]i[/latex] six de suite en lançant [latex]i[/latex] fois le dé c'est-à-dire qu'en lançant [latex]i[/latex] fois le dé à chaque fois, [latex]U_i[/latex] est le nombre de fois qu'il faut le faire pour obtenir [latex]i[/latex] six.

La somme vient du fait que pour obtenir n six de suite, il faut préalablement obtenir 1, 2, ..., n-1 six de suite. Il faut donc comptabiliser toutes les fois qu'il faudra pour obtenir des séries intermédiaires de 1 à n.

titoufred · #115

Je ne comprends toujours pas ton raisonnement. Restons-en à [latex]n=2[/latex] pour l'instant. Pourquoi faut-il ajouter 6 et 36 ?

kossi_tg · #116

Pour faire un 6-6, il faut procéder en 2 temps:
*** Arriver à avoir un 1er six: 6 lancers,
*** A chacun de ces 6 lancers, il y a 6 autres lancers associés: 36 lancers à la recherche du 2ième six.

Le tableau ci-après décrit la situation. Le double 6 cherché est marqué en gras. Le nombre de lancers est la taille du tableau : 6+36.

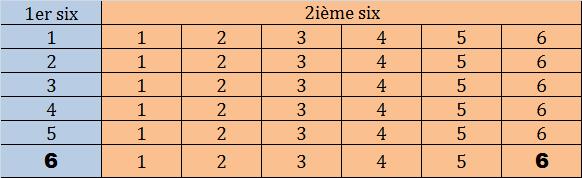
Spoiler : [Afficher le message]

titoufred · #117

Je ne te suis pas mais peu importe.

Voici mon point de vue :

J'aurais plutôt mis les cases rouges à gauche pour représenter le 1er six, et les cases bleues à droite pour représenter le 2ème six.

Pour réussir le 1er six, on va faire en moyenne 6 lancers. Une fois le premier six réussi, on va tenter une première fois le 2ème six, que l'on va rater. Et l'on recommence alors à tenter le 1er six, etc... Ce n'est qu'à la sixième tentative du 2ème six qu'on va le réussir.

Ce qui donne donc la série de longueur moyenne suivante pour obtenir 66 :

123456-1-123456-2-123456-3-123456-4-123456-5-123456-6

De manière générale, si l'on note [latex]E_n[/latex] le nombre de lancers moyens pour obtenir [latex]n[/latex] six, en raisonnant de la même manière on voit que [latex]E_{n+1}=6E_n + 6[/latex]. Ce qui permet de conclure facilement que [latex]E_n = 6^n + ... + 6[/latex].

kossi_tg · #118

On interprète les mêmes faits exactement de la même manière; la seule différence est que tu mets B+A alors que je mets A+B. Tout dépend de la formulation intuitive des faits. Je ne vois pas pourquoi tu n'arrive pas à suivre

titoufred · #119

kossi, saurais-tu répondre aux questions restées sans réponses tout au long de ce fil ?

Par exemple, quel est le nombre moyen de lancers pour obtenir "665" ? Et pour "656" ? Et "566" ?

PRINCELEROI · #120

titou:peux-tu me dire quelle est la probabilité que chaque face d'un dé à six faces sorte une fois en six lancers?
Ca m'intéresse!

SabanSuresh · #121

La probabilité que chaque face d'un dé à six faces sorte une fois en six lancers est de 1 : 1/6*6 (chaque face à 1 chance sur 6 de tomber à chaque lancers).

PRINCELEROI · #122

Saban:j'ai 6/6 chance d'avoir une face quelconque au premier lancer puis 5 sur 6 d'en avoir une autre au deuxième puis 4 sur 6 d'en avoir une autre au troisième etc...
Soit 5!/6^5= 120/7776.Même pas 2%!
Enfin je pense mais titou va nous dire!

Nombrilist · #123

Pas besoin de Titou, c'est évident que c'est bon ^^.

titoufred · #124

Plus d'un an après, ces questions résistent :

1) Combien de lancers faut-il en moyenne pour voir apparaître "665" ?

2) Combien de lancers faut-il en moyenne pour voir apparaître "566" ?

3) Combien de lancers faut-il en moyenne pour voir apparaître "656" ?

4) Combien de lancers faut-il en moyenne pour voir apparaître une séquence quelconque dans le cas général ?

Bon week-end !

nodgim · #125

Salut Titoufred,
N'ayant pas suivi cette discussion au départ, 665 désigne t'il 6 puis 6 puis 5 consécutifs ?
Merci pour cette précision.

Forum dédié aux énigmes et à toutes formes de jeux de logique.	Déconnexion
Tu n'es pas identifié sur Prise2tete : s'identifier. Accueil Forum	[+]

#101 - 10-06-2013 11:56:41

Combien de lancers de dé aavnt de... ?

#0 Pub

#102 - 10-06-2013 12:22:56

Combien de laancers de dé avant de... ?

#103 - 10-06-2013 15:16:06

Combien de lancesr de dé avant de... ?

#104 - 10-06-2013 18:35:54

Combieen de lancers de dé avant de... ?

#105 - 10-06-2013 18:43:58

Combien de lancerss de dé avant de... ?

#106 - 10-06-2013 18:50:10

combien de lancers de dé avabt de... ?

#107 - 10-06-2013 18:57:05

Combien de lancers de déé avant de... ?

#108 - 10-06-2013 19:36:44

Combien de lancers de dé avannt de... ?

#109 - 10-06-2013 19:41:08

Combie nde lancers de dé avant de... ?

#110 - 13-06-2013 00:14:44

Combien de lancers d edé avant de... ?

#111 - 18-11-2013 16:21:34

combien de lancers fe dé avant de... ?

#112 - 18-11-2013 20:03:19

Combien de lancers de dé avantt de... ?

#113 - 20-11-2013 01:42:10

combien de lancers dr dé avant de... ?

#114 - 20-11-2013 22:08:31

Combien de lancesr de dé avant de... ?

#115 - 20-11-2013 23:09:28

combien de lancerq de dé avant de... ?

#116 - 20-11-2013 23:45:39

Combien de lancers de dé avant de.. ?

#117 - 21-11-2013 01:09:14

colbien de lancers de dé avant de... ?

#118 - 21-11-2013 07:54:24

combien de lancers de dé avant se... ?

#119 - 21-11-2013 14:38:55

Combien de lancers de dé aavant de... ?

#120 - 21-11-2013 20:25:39

combien de mancers de dé avant de... ?

#121 - 21-11-2013 20:57:44

cpmbien de lancers de dé avant de... ?

#122 - 21-11-2013 21:05:30

Combine de lancers de dé avant de... ?

#123 - 21-11-2013 23:04:22

Coombien de lancers de dé avant de... ?

#124 - 07-03-2015 11:11:32

Combien de lancers dde dé avant de... ?

#125 - 07-03-2015 11:17:01

Combien d lancers de dé avant de... ?

Réponse rapide

Sujets similaires

Mots clés des moteurs de recherche

Pied de page des forums