|
#1 - 04-05-2013 22:06:49
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Mthématiques pour les nuls 13
Une petite pour la route, pas trop difficile...
Considérons un cercle C1 de centre (0,0) et de rayon 1.
On construit un cercle C2 de centre (0,0) et de rayon x.
On trace une droite (d), passant par le centre des deux cercles et coupant ces deux cercles respectivement en C pour C1 et en D pour C2
On place les points A(1,0) et B(x,0)
Montrer que AD=BC
Bon amusement,
Shadock 
PS : La meilleure solution que j'ai pour le moment et justifiée on ne peut plus soigneusement tient en 2 lignes.
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#2 - 04-05-2013 22:52:53
- gwen27
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 6,193E+3
mathématiques poir les nuls 13
Par symétrie de la construction, OA +AD = OC+CB ; OA=OC donc AD=CB
#3 - 04-05-2013 23:15:47
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
mathélatiques pour les nuls 13
Bonsoir
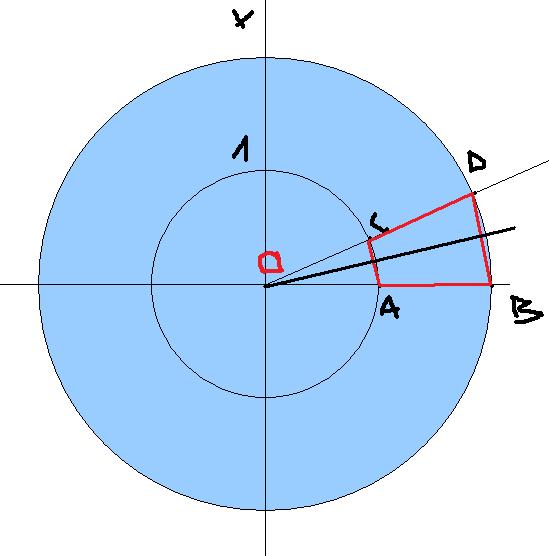
Il est clair que (AC)//(BD) et AB=CD donc ABDC est un trapèze isocèle .
Vasimolo
#4 - 04-05-2013 23:50:47
- looozer
- Expert de Prise2Tete
- Enigmes résolues : 49
- Messages : 697
- Lieu: Belgique
Mathématiqeus pour les nuls 13
Les points A,D et B,C forment avec le centre des triangles isométriques (angle commun compris entre des côtés de longueurs 1 et x).
[AD] et [BC] ont donc aussi même longueur.
#5 - 05-05-2013 01:10:26
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Mathématiques pour lles nuls 13
Je vois plusieurs façons de le voir :
1) Soit justifier l'axe de symétrie passant par O et le point d'intersection de [AD] et [BC] :
OBD est un triangle isocèle de sommet principal O car OB=OD, donc sa bissectrice issue de O est un axe de symétrie.
De même pour OAC, qui a la même bissectrice pour axe de symétrie puisque O, A et B sont alignés, ainsi que O, C et D et dans le même ordre.
La symétrie axiale conserve les distances et [BC] et le symétrique de [AD] par rapport à l'axe de symétrie commun, donc BC=AD
2) Soit utiliser la réciproque de Thalès qui montre que (AC)//(BD) car OA/OB=1/x=OC/OD, et comme AB=|x-1|=CD, ABDC est un trapèze isocèle non parallèlogramme dont les diagonales AD et BC font donc la même longueur.
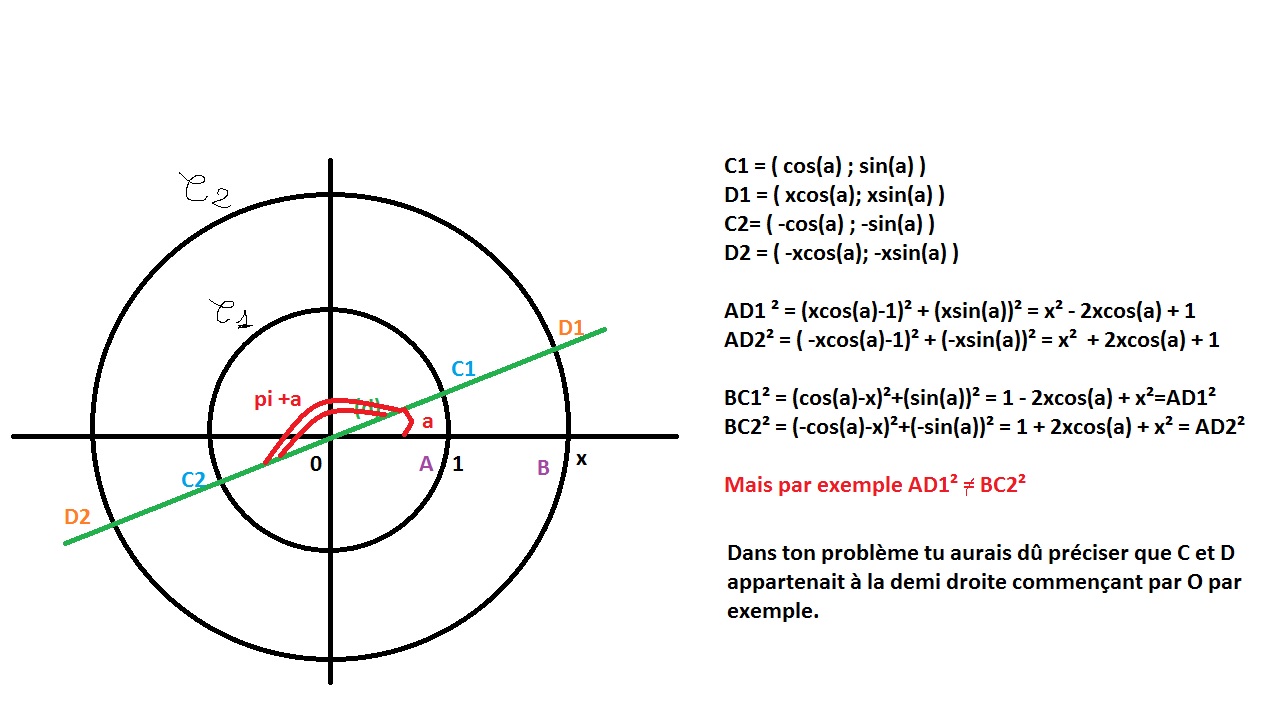
3) Soit calculer les distances cartésiennes : si on considère l'angle "a" que fait (d) avec l'axe (Ox),
C(cosa;sina) et D(x.cosa;x.sina) (avec A(1,0) et B(x,0))
Alors AD²=(x.cosa-1)²+x².sin²a = x².cos²a-2x.cosa+1+x².sin²a = 1+x²-2x.cosa
et BC²=(cosa-x)²+sin²a = cos²a-2x.cosa+x²+sin²a = 1+x²-2x.cosa
On retrouve AD²=BC² donc AD=BC
#6 - 05-05-2013 11:42:54
- titoufred
- Elite de Prise2Tete
- Enigmes résolues : 20
- Messages : 1749
Mathématiques pour les nnuls 13
On appelle s la symetrie orthogonale par rapport a la bissectrice de l'angle AOC. Alors s(A)=C et s(D)=B donc s([AD])=[CB] et donc AD=BC.
#7 - 05-05-2013 12:34:09
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
mathématisues pour les nuls 13
Evidemment que des bonnes réponses pour le moment 
J'ai aussi trouvé une solution beaucoup moins évidente mais qui se passe de toute notion de géométrie 
Shadock
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#8 - 05-05-2013 12:39:40
- Vasimolo
- Le pâtissier
- Enigmes résolues : 49
- Messages : 5,448E+3
Mathématiques ppour les nuls 13
On peut aussi remarquer que [BC] est le symétrique de [AD] par rapport à la bissectrice de BÂD .
Vasimolo
#9 - 05-05-2013 15:56:42
- golgot59
- Elite de Prise2Tete
- Enigmes résolues : 48
- Messages : 1494
- Lieu: Coutiches
Mathématiques our les nuls 13
Il y a aussi la formule d'Al Kashi :
BC²=OB²+OC²-2OB.OC.cosBÔC
AD²=OD²+OA²-2OA.OD.cosAÔD
Et comme OB=x=OD, OA=1=OC et BÔC=AÔD : BC²=AD² donc BC=AD
#10 - 05-05-2013 16:08:13
- Jackv
- Elite de Prise2Tete
- Enigmes résolues : 34
- Messages : 3614
- Lieu: 94110
mathémztiques pour les nuls 13
En une ligne (en appliquant 2 fois la formule a² = b² = c² - 2 bc cos (A) on trouve :
AD² = BC² = 1 + x² - 2x cos (AOC)
#11 - 05-05-2013 18:00:46
- PRINCELEROI
- Elite de Prise2Tete
- Enigmes résolues : 33
- Messages : 1275
mathématiques pour les nums 13
Au pif
AD et BC sont les hypoténuses du même triangle.
#12 - 05-05-2013 18:23:51
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Mathématiques pour les nul 13
Il faut prendre pour (d) une demi-droite, sinon l'énoncé est faux !
La figure est symétrique par rapport à la bissectrice intérieure [latex]\Delta[/latex] de l'angle [latex]\widehat{AOC}[/latex] ; comme la symétrie par rapport à [latex]\Delta[/latex] transforme A en C et D en B, on a donc AD=BC.
#13 - 05-05-2013 23:11:06
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
Mathéamtiques pour les nuls 13
@PRINCELEROI c'est une idée mais il faut la justifier 
@masab Oui c'est ça, pour la demi-droite je ne vois pas pourquoi...
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#14 - 06-05-2013 01:26:28
- Tofic
- Passionné de Prise2Tete
- Enigmes résolues : 29
- Messages : 72
Mathématiques pour les nuuls 13
Salut, après avoir tracé la figure, on imagine facilement qu'il doit y avoir tout un tas de solutions au problème. Le soucis est de le démontrer  . .
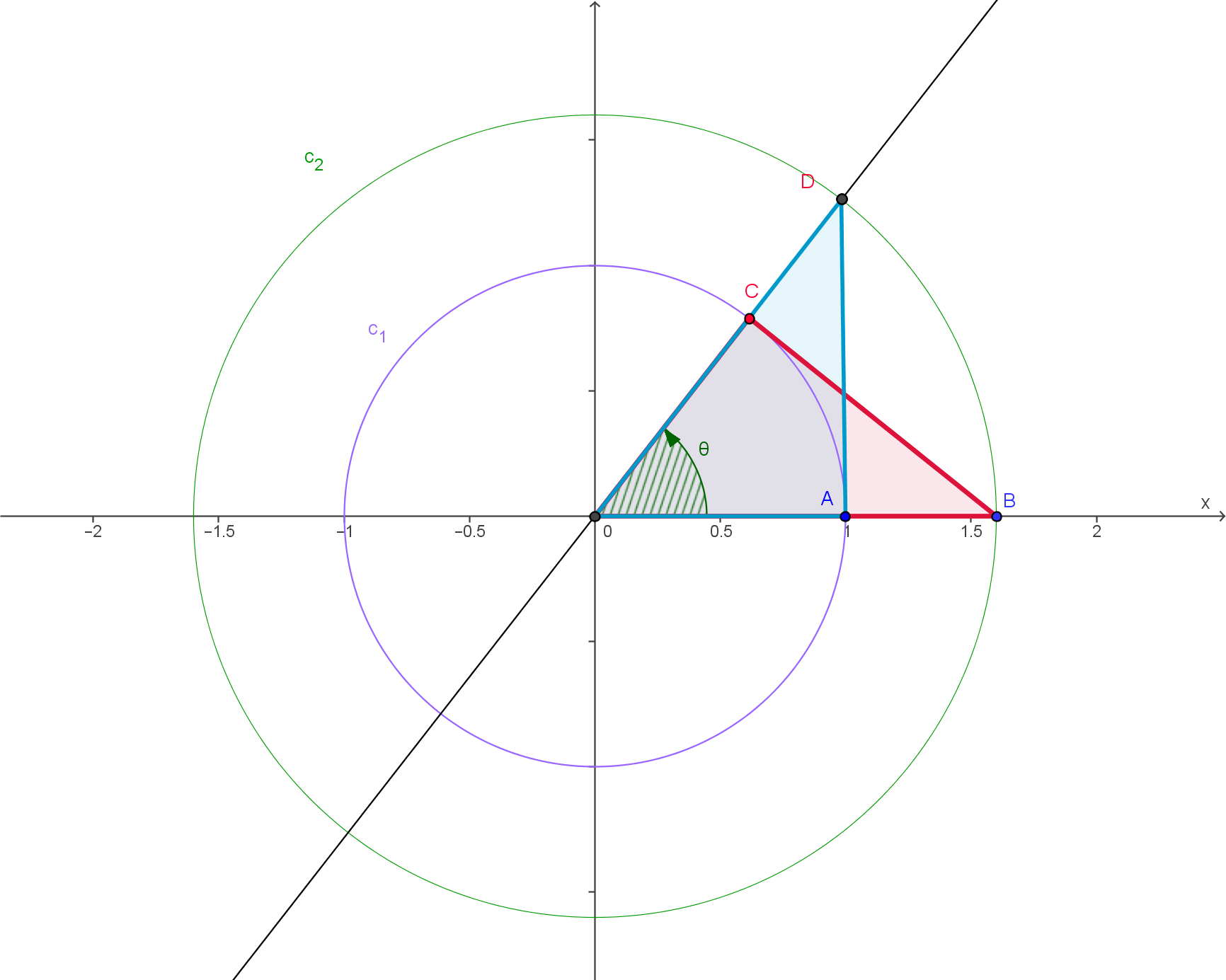
J'ai remarqué, deux triangles qui comporte les droites en questions et qui semble bien coller avec le théorème d'Al-Kashi. Appliquons ça au problème.
Soit deux triangles [latex]oCB[/latex] et [latex]oDA[/latex] avec
[TeX]\theta=\widehat{CoB}=\widehat{DoA}[/TeX][TeX]\overline{oB}=\overline{oD}=x[/latex] (rayon du cercle),
[latex]\overline{oC}=\overline{oA}=1[/TeX]
on trouve:
[TeX]\overline{CB}=\sqrt{x^2+1-2x.cos{\theta}}[/TeX]
[TeX]\overline{AD}=\sqrt{x^2+1-2x.cos{\theta}}[/TeX]
Donc, si je n'ai pas fait de bêtises, quelque soit le rayon [latex]x[/latex] et l'angle [latex]\theta[/latex], les droites [latex]AD[/latex] et [latex]BC[/latex] sont égales.
#15 - 06-05-2013 12:10:10
- SabanSuresh
- Elite de Prise2Tete
- Enigmes résolues : 45
- Messages : 1951
- Lieu: Paris
Mathémaitques pour les nuls 13
Je ne sais pas le démontrer mais j'ai appris que les diagonales d'un trapèze isocèle sont égales. Or les droites (AC) et (BD) sont parallèles et CD=AB=x-1. Donc ABCD est un trapèze isocèle et AD=BC.
#16 - 06-05-2013 12:10:56
- masab
- Expert de Prise2Tete
- Enigmes résolues : 44
- Messages : 971
Mathématiques pour les nuls 1
La droite (d) coupe le cercle C1 en 2 points... Donc il y a un choix à faire pour C ; de même pour D. Certains choix ne respectent pas AD=BC !
#17 - 06-05-2013 14:44:00
- Klimrod
- Elite de Prise2Tete
- Enigmes résolues : 40
- Messages : 4054
- Lieu: hébesphénorotonde triangulaire
Mathématiques pourr les nuls 13
Bonjour,
Si l'on trace la bissectrice entre la droite d et l'axe des x, alors les segments AB et CD sont symétriques par rapport à cette bissectrice et donc AD = BC
Même pas deux lignes !
Klim.
J'ai tant besoin de temps pour buller qu'il n'en reste plus assez pour bosser. Qui vit sans folie n'est pas si sage qu'il croit.
#18 - 06-05-2013 15:16:56
- kossi_tg
- Professionnel de Prise2Tete
- Enigmes résolues : 18
- Messages : 307
- Lieu: Montargis
Mathématiques pou les nuls 13
Deux solutions parmi tant d'autres:
Solution 1:
Soit (d') la bissectrice de l'angle [latex]\widehat{AOC}[/latex] avec O l'origine du repère. C et B sont respectivement des symétries orthogonales de A et D par rapport à (d'); CB=AD car la symétrie conserve les distances.
Solution 2:
Soit a l'angle entre les droites (d) et (AB)
s et c respectivement le sinus et le cosinus de a
les coordonnées des points C et D:
C (c, s)
D(x*c, x*s)
Après un simple calcul de distance, on a:
[TeX]AD=BC=\sqrt{1+x^2-2*x*c}[/TeX]
#19 - 06-05-2013 17:12:22
- gilles355
- Professionnel de Prise2Tete
- Enigmes résolues : 49
- Messages : 421
Mathématqiues pour les nuls 13
#20 - 06-05-2013 19:45:15
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
mathématiques pour lrs nuls 13
Et encore moult bonnes réponses 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
#21 - 06-05-2013 21:50:03
- Tofic
- Passionné de Prise2Tete
- Enigmes résolues : 29
- Messages : 72
Mathématiques pour lles nuls 13
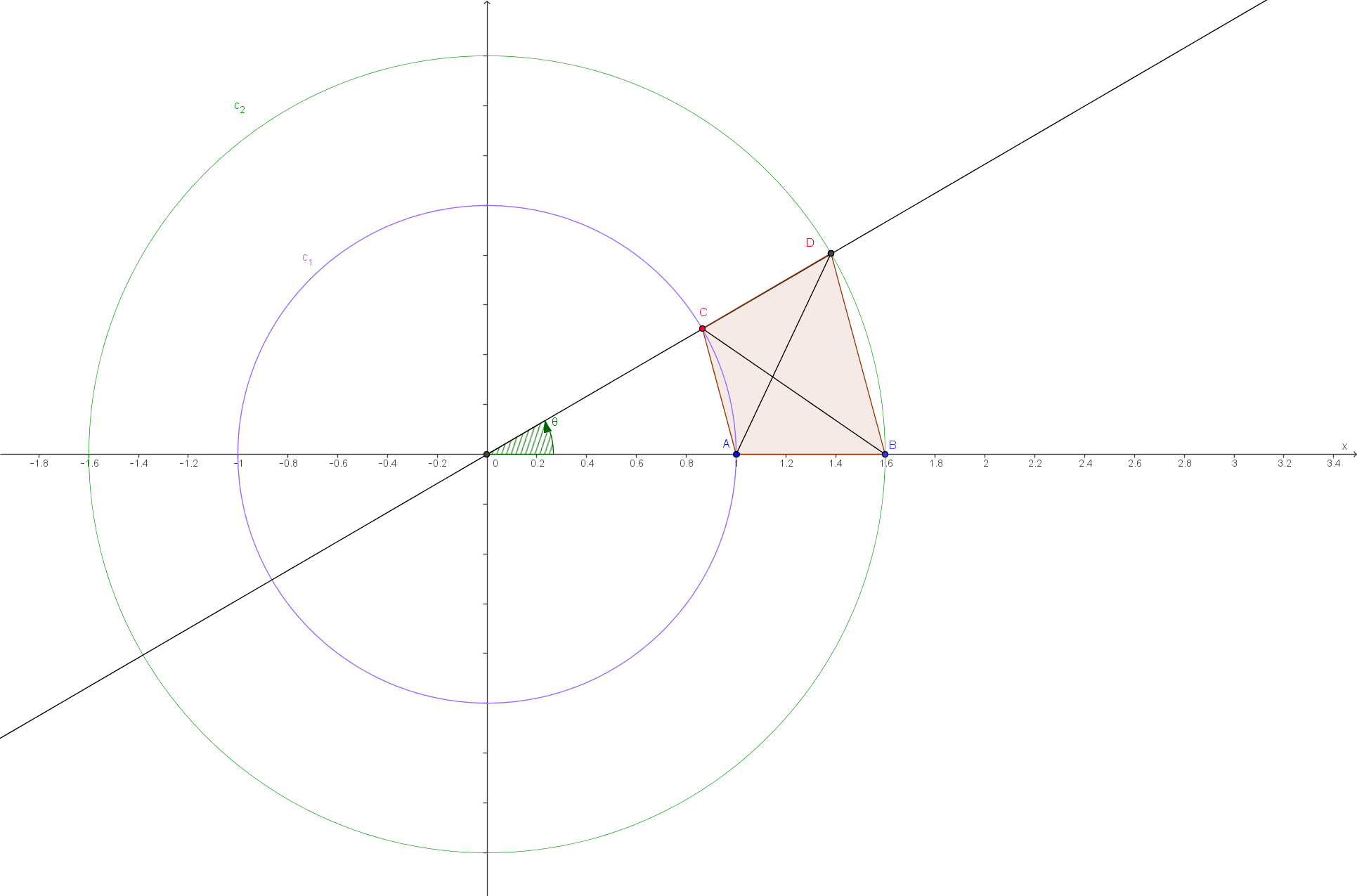
Je me demandes même si en allant voir du coté de Thalès, je ne trouverais pas quelques bigorneaux sous le rocher.
Une autre figure remarquable:
#22 - 06-05-2013 22:01:30
- Franky1103
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 3238
- Lieu: Luxembourg
mathématiques ppur les nuls 13
Le demi-axe des abscisses Ox et la demie-droite Od sont symétriques par rapport à leur bissectrice. Donc les vecteurs AB et CD aussi. Donc AD = BC.
#23 - 07-05-2013 11:38:38
- MthS-MlndN
- Hors d'u-Sage
- Enigmes résolues : 49
- Messages : 12,414E+3
- Lieu: Rouen
Mathémmatiques pour les nuls 13
La droite en question va couper chaque cercle en deux points, pas en un seul. Quel point choisir ?
Podcasts Modern Zeuhl : http://radio-r2r.fr/?p=298
#24 - 07-05-2013 22:17:01
- bidipe
- Elite de Prise2Tete
- Enigmes résolues : 49
- Messages : 1126
- Lieu: Côte basco-landaise
Mathématiqes pour les nuls 13
Les points C et A sont sur le cercle C1
Les points B et D sont sur le cercle C2
A et B sont sur une droite passant par le centre des cercles
C et D sont sur une droite passant par le centre des cercles
=> si l'on compare les triangles ACD et ACB :
Ils ont un côté commun AC (corde du cercle C1)
et les cotés AB et CD sont égaux par construction des 2 cercles concentriques
Les angles DCA et CAB sont égaux
Les 2 triangles sont donc isométriques
Donc leurs 3emes côtés sont égaux : AD = BC
Bon, ok, ca fait 35 ans que je n'ai pas fait de démonstration mathématique 
#25 - 08-05-2013 12:30:54
- shadock
- Elite de Prise2Tete
- Enigmes résolues : 39
- Messages : 3334
mathématiques pour les nils 13
Alors maintenant voici une réponse possible aussi en utilisant les nombres complexes

Soient [latex]x \in \mathbb{R}[/latex] et [latex]u \in \mathbb{C}[/latex] et [latex]|u|=1[/latex]
Alors on a [latex]|x-u|=|u\left(\frac{x}{u}-1\right)|=|\left(\frac{x}{u}-1\right)|=|x\bar{u}-1|=|1-xu|[/latex] d'où le résultat.
Bravo à tous et merci !
Shadock 
"L'expérience est une lanterne qui n'éclaire que celui qui la porte." L-F. Céline
Mots clés des moteurs de recherche
|
 |

 Accueil
Accueil
 Forum
Forum