Je trouve 1.087032884, soit 2pi-3sqrt(3)

douze fois la différence entre l'aire d'un sixième de cercle et celle d'un triangle équilatéral.

12 ( Pi/6 - 3^(1/2)/4) = 2 Pi - 3^(3/2)

Soit R l'aire de la Rosace.
Soit H l'aire de l'Hexagone régulier ci-dessus.

Dans l'image en haut à gauche soit A = aire en bleu = air en jaune = air en rouge.
On a R = H - 3A.

L'image en haut à droite montre que H est six fois l'aire du triangle équilatéral gris et de côté 1.
autrement écrit :    [latex] H = 6*{{\sqrt 3}\over 4} = {{3\sqrt 3}\over 2}[/latex]

Et l'image du bas montre que A est égale à H moins l'aire des deux secteur angulaire en gris.
L'aire d'un secteur angulaire de rayon r et d'angle  [latex]\theta[/latex]  (en radian) est   [latex]r^2*{\theta\over 2}[/latex].
Ici r = 1 et l'hexagone étant régulier on a  [latex]\theta={{2\pi}\over 3}[/latex]  , donc l'air d'un secteur angulaire gris est :  [latex]\pi\over 3[/latex].
Donc on a   [latex]A=H-2*{\pi\over 3}[/latex].

Et donc l'aire de la rosace est de :  [latex]R=H-3(H-{{2\pi}\over 3})=2\pi -2H[/latex], et en remplaçant H par sa valeur calculer précédemment on a :
[TeX]R=2\pi -3\sqrt 3[/TeX]


EDIT : En fait il y a plus simple : dans l'image en haut à droite, le triangle équilatéral gris et une demi-pétale de rosace verte forment un secteur angulaire d'angle  [latex]\pi\over 3[/latex]   (car le triangle est équilatéral) et donc d'air   [latex]\pi\over 6[/latex].
Donc  l'air de la demi-pétale de rosace est l'air du secteur angulaire ci-dessus moins l'air du
triangle équilatéral, i.e   [latex]{\pi\over 6}-{{\sqrt 3}\over 4}[/latex].

La rosace ayant 6 pétale soit douze demi-pétales à pour aire :
                          [latex]12({\pi\over 6}-{{\sqrt 3}\over 4})=2\pi -3\sqrt 3[/latex].

a vrai dire je suis au college donc j'aurai du mal a repondre:( mais je crois savoir/
l'aire d'un hexagone inscriptible dans un cerle de 2 cm est egale a 5;196...
ON REMARQUE QUE LES RESTES  autour de l'hexagone represente trois branche
donc
(2pi)-5.196...=1.087032884
multiplié par deux comme il y a 6 branches, cela donne 2.174065769


Conclusion
L'aire de la fleur est de 2,174065769
L'aire du reste est egale a 4,109119538
L'aire du cercle ezst egale a 2pi

Bonjour à tous,

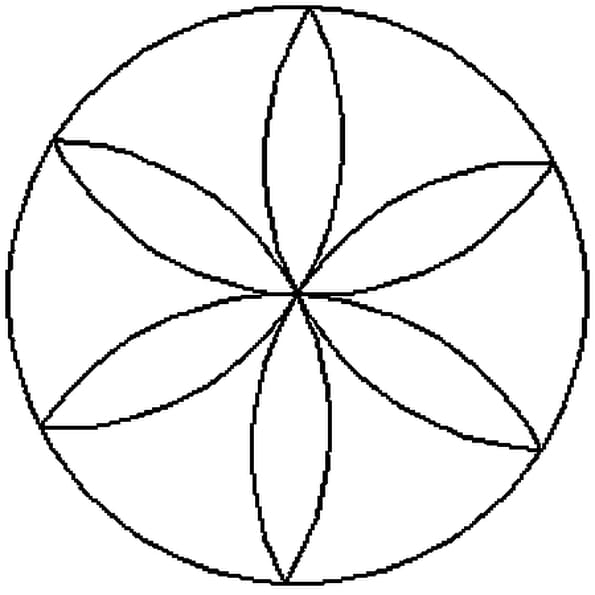
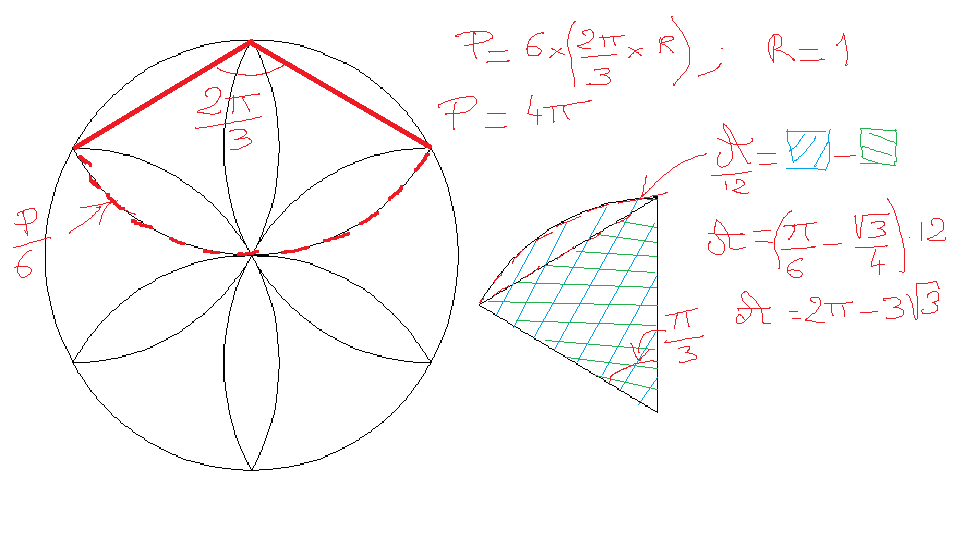
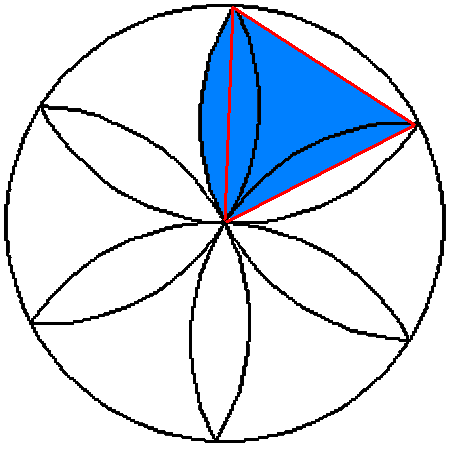
Je commence par tracer la rosace dans un cercle de rayon 1. Pour simplifier le travail (symétrie oblige...), je découpe mon gâteau en six parts égales (ceci n'est absolument pas un remake des énigmes de qui vous savez). Pour la découpe, les arrêtes du gâteau correspondent aux sommets de la rosace. Je ne travaille plus que sur la portion suivante dans laquelle je trace un triangle équilatéral de côté 1:



La part du gâteau a une aire égale à pi/6.

Le triangle rectangle a une aire égale à V3/4.

Par différence, on trouve l'aire du "petit morceau qui reste" (en vert) : pi/6-V3/4

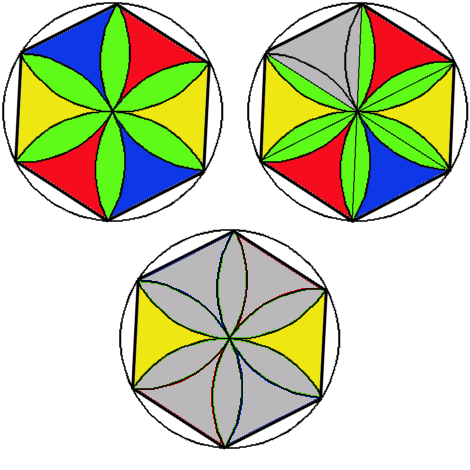
Or lorsqu'on observe la rosace, on constate qu'elle est composée de 6 pétales identiques et chacun de ces pétales est composé de 2 demi-pétales (ça s'invente pas). Or ces demi-pétales ont exactement la même aire que notre "petit morceau qui reste". Pour s'en convaincre il suffit de construire une seconde rosace, identique à la première, en y intégrant notre "petit morceau qui reste"...

La rosace étant composé de 12 de ces demi-pétales, on ontient une aire pour la rosace de 12*(pi/6-V3/4) soit 2pi-3V3 !

Surface où l'on cherche le rayon pour trouver le volume: je pense qu'il s'agit d'un jeu de mots pouvant désigner une librairie (surface où on doit trouver dans un rayon de classement un livre alias volume!)

Ce n'est pas une réponse à la question 1mais une énigme que l'on m'a posée et dont j'ai essayé de trouver la réponse? Qu'en penses-tu?